Лекция 1. Многие гидросистемы имеют несколько гидродвигателей, питаемые от одного насоса

Многие гидросистемы имеют несколько гидродвигателей, питаемые от одного насоса. При такой схеме возможны два варианта подключения гидродвигателей.

Гидросистема с параллельным включением гидропривода показана на рис.10.10. Гидросистема имеет одну общую насосную станцию 1 и три гидроцилиндра 2, 3 и 4. Каждый из гидроцилиндров имеет собственное независимое устройство управления - гидрораспределители 6, 7 и 8. В точке 5 гидролиния имеет разветвление, в котором общая подача насосной станции 1 делится на три части Q₁, Q₂ и Q₃ . Каждый из гидроцилиндров может включаться в работу в любой момент времени, независимо от других потребителей, и совершать как холостой, так и рабочий ход.

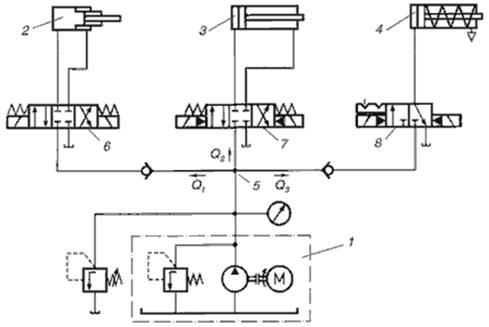
Рис.10.10 Гидросистема параллельным включением гидропривода

Гидросистема с последовательным включением гидропривода представлена на ри.10.11. Гидросистема имеет два гидроцилиндра 1 и 2, которые питаются от общей насосной станции 3. В отличие от гидросистемы с параллельным включением, гидроцилиндр 2 может осуществлять рабочий ход только при неработающем первом гидроцилиндре, поскольку при включении гидроцилиндра 1, напорная линия цилиндра 2 становится сливной, в которой давление падает. При этом цилиндр 2 может осуществлять только холостой ход.

Гидросистемы с параллельным включением гидропривода получили наибольшее распространение. Однако, показанная на рис.10.10 гидросхема имеет один существенный недостаток.

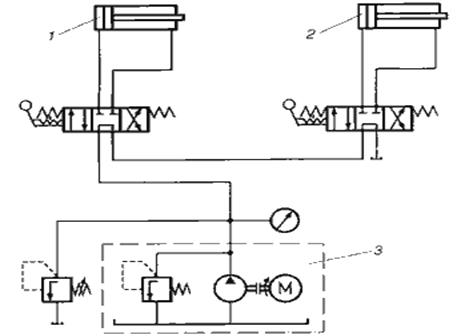
Рис.10.11 Гидросистема последовательным включением гидропривода.

Дело в том, что при включении всех трех гидроцилиндров скорость перемещения их выходных звеньев будет минимальна. Если отключить один из них, например первый (2), то скорость у второго и третьего возрастет, так как общая подача будет делиться только на Q₂ и Q₃. Чтобы этого избежать, в гидросистему необходимо включать редукционные клапаны. На рис.10.12 представлена схема гидросистемы с одним насосом 3 и двумя силовыми цилиндрами 1 и 6, один из которых (цилиндр 6) рассчитан на работу при внешней нагрузке (давлении), значительно меньшей нагрузки второго цилиндра 1.

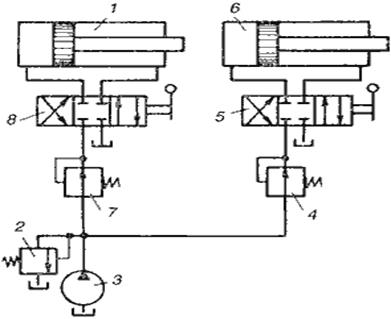
Рис.10.12 Гидросистема с двумя гидроцилиндрами, питаемыми
одним наосом через редукционные клапаны

.

Для снижения давления в системе питания цилиндра 6 до требуемой величины применен редукционный клапан 4, установленный на входе в распределитель 5. Для цилиндра 1 также предусмотрен редукционный клапан 7, отрегулированный на рабочее давление в этом цилиндре. Редукционный клапан 7 также устанавливается на входе в распределитель 8, управляющий цилиндром 1. Насос 3 снабжен переливным клапаном 2, который сбрасывает излишек рабочей жидкости в бак.

Лекция 1.

Функции нескольких переменных. Геометрическое изображение функции двух переменных. Линии и поверхности уровня. Предел и непрерывность функции нескольких переменных, их свойства. Частные производные, их свойства и геометрический смысл.

Определение 1.1. Переменная z (с областью изменения Z)называется функцией двух независимых переменных х,у в множестве М, если каждой паре (х,у) из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.

Определение 1.2. Множество М, в котором заданы переменные х,у, называется областью определения функции, а сами х,у – ее аргументами.

Обозначения: z = f(x,y), z = z(x,y).

Примеры.

1. z = xy, z = x² + y² - функции, определенные для любых действительных значений х,у.
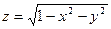2. - функция, областью определения которой являются решения неравенства .

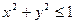Замечание. Так как пару чисел (х,у) можно считать координатами некоторой точки на плоскости, будем впоследствии использовать термин «точка» для пары аргументов функции двух переменных, а также для упорядоченного набора чисел 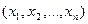, являющихся аргументами функции нескольких переменных.

Определение 1.3. . Переменная z (с областью изменения Z)называется функцией нескольких независимых переменных 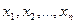в множестве М, если каждому набору чисел 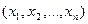из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов и области определения вводятся так же, как для функции двух переменных.

Обозначения: z = f 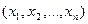, z = z .

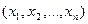Геометрическое изображение функции двух переменных.

Рассмотрим функцию z = f(x,y), (1.1)

определенную в некоторой области М на плоскости Оху. Тогда множество точек трехмерного пространства с координатами (x,y,z), где 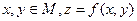, является графиком функции двух переменных. Поскольку уравнение (1.1) определяет некоторую поверхность в трехмерном пространстве, она и будет геометрическим изображением рассматриваемой функции.

z

z = f(x,y)

M y

Примерами могут служить изучаемые в предыдущем семестре уравнения плоскости

z = ax + by + c

и поверхностей второго порядка:

z = x² + y² (параболоид вращения),

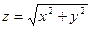(конус) и т.д.

Замечание. Для функции трех и более переменных будем пользоваться термином «поверхность в n-мерном пространстве», хотя изобразить подобную поверхность невозможно.

Линии и поверхности уровня.

Для функции двух переменных, заданной уравнением (1.1), можно рассмотреть множество точек (х,у) плоскости Оху, для которых z принимает одно и то же постоянное значение, то есть z = const. Эти точки образуют на плоскости линию, называемую линией уровня.

Пример.

Найдем линии уровня для поверхности z = 4 – x² - y². Их уравнения имеют вид x² + y² = 4 – c (c=const) – уравнения концентрических окружностей с центром в начале координат и с радиусами 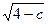. Например, при с=0 получаем окружность x² + y² = 4 .

Для функции трех переменных u = u (x, y, z) уравнение u (x, y, z) = c определяет поверхность в трехмерном пространстве, которую называют поверхностью уровня.

Пример.

Для функции u = 3x + 5y – 7z –12 поверхностями уровня будет семейство параллельных плоскостей, задаваемых уравнениями 3x + 5y – 7z –12 + с = 0.