Формула Тейлора для функции нескольких переменных.
Как известно, функцию F(t) при условии существования ее производных по порядок n+1 можно разложить по формуле Тейлора с остаточным членом в форме Лагранжа (см. формулы (21.7), (21.11) первой части курса). Запишем эту формулу в дифференциальной форме:
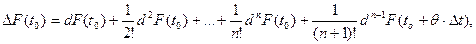 (4.3)
(4.3)
где 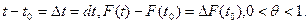
В этой форме формулу Тейлора можно распространить на случай функции нескольких переменных.
Рассмотрим функцию двух переменных f(x, y), имеющую в окрестности точки (х0 , у0) непрерывные производные по (n + 1)-й порядок включительно. Зададим аргументам х и у некоторые приращения Δх и Δу и рассмотрим новую независимую переменную t:
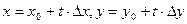 (0 ≤ t ≤1). Эти формулы задают прямолинейный отрезок, соединяющий точки (х0 , у0) и (х0 + Δх, у0 + Δу). Тогда вместо приращения Δf (x0 ,y0) можно рассматривать приращение вспомогательной функции
(0 ≤ t ≤1). Эти формулы задают прямолинейный отрезок, соединяющий точки (х0 , у0) и (х0 + Δх, у0 + Δу). Тогда вместо приращения Δf (x0 ,y0) можно рассматривать приращение вспомогательной функции
F(t) = f (x0 + t Δx, y0 + tΔy) , (4.4)
равное ΔF (0) = F (1) – F (0). Но F (t) является функцией одной переменной t, следовательно, к ней применима формула (4.3). Получаем:
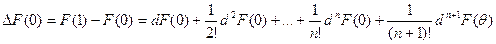 .
.
Отметим, что при линейной замене переменных дифференциалы высших порядков обладают свойством инвариантности, то есть
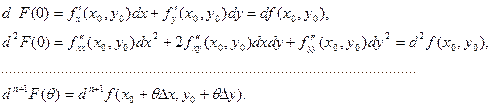
Подставив эти выражения в (4.3), получим формулу Тейлора для функции двух переменных:
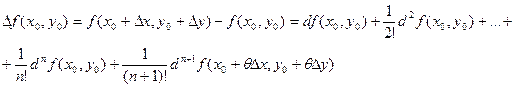 , (4.5)
, (4.5)
где 0<θ<1.
Замечание. В дифференциальной форме формула Тейлора для случая нескольких переменных выглядит достаточно просто, однако в развернутом виде она весьма громоздка. Например, даже для функции двух переменных первые ее члена выглядят так:

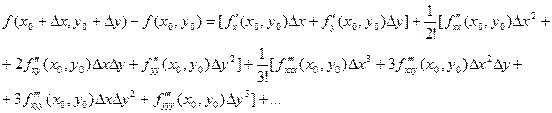
Дата добавления: 2015-03-19; просмотров: 1134;
