Существование энтропии у реальных (не идеальных) газов

Как уже отмечалось (раздел 2) для реальных (не идеальных) газов уравнением Клапейрона (2.1) пользоваться нельзя. Уравнение состояния для этих газов имеет другой вид, например, вид уравнения Ван-дер-Ваальса (2.5):

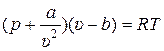. (1)

Докажем существование энтропии у газа, уравнение состояния которого имеет вид (1). Для этого запишем уравнение первого закона термодинамики и сразу обе части уравнения разделим на Т:

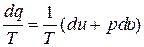. (2)

Из (1) выразим р и подставим в (2), одновременно раскрыв дифференциал du (T, υ):

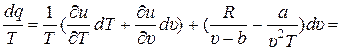
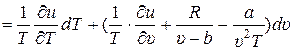. (3)

Из математики известно, что необходимым и достаточным условием того, чтобы правая часть являлась полным дифференциалом некоторой непрерывной функции двух переменных Т и υ, то есть была бы равна ds (T, υ), является выполнение следующего равенства:

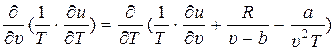. (4)

При выполнении дифференцирования в правой части средний член исчезает, а последний даёт 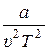. Из первого члена возникают два выражения, первое из которых взаимно уничтожается с левой частью, в то время как второе равно – 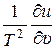. Таким образом, уравнение (4) принимает вид:

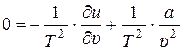. (5)

Из (5) получаем:

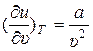. (6)

Выражение (6) показывает, как у реальных газов внутренняя энергия зависит от удельного объёма. (Напомним, что у идеальных газов эта зависимость отсутствует: .)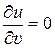

Таким образом, при условии, что выражение (6) выполняется, можно утверждать, что в правой части (3) будем иметь:

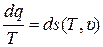, (7)

где s – некоторая непрерывная функция двух параметров состояния Т и υ, то есть функция состояния, Дж/(кг·К).

Полученное выражение (7) является доказательством существования энтропии у реальных газов, имеющих уравнение состояния (1).

Аналогичным образом доказывается существование энтропии для общего случая у реальных газов, для которых эмпирические уравнение состояния имеет вид:

p = f (υ, T). (8)

где f (υ, T) – некоторая известная функция υ и Т.

6.2. Существование энтропии у систем, находящихся в жидком или твёрдом состояниях

В процессах нагрева или охлаждения при постоянном давлении тела, находящиеся в жидком или твёрдом состояниях, можно рассматривать как практически не сжимаемые. То есть все процессы, которые с ними происходят можно считать происходящими при постоянном удельном объёме υ = const. Соответственно dυ = 0.

Для такого случая первый закон термодинамики принимает вид:

du = dq – p dυ = dq

или (9)

dq = du.

Как уже отмечалось, в силу несжимаемости удельные истинные теплоёмкости при постоянном давлении и постоянном объёме у твёрдых и жидких тел практически равны. Таким образом, для любого процесса, происходящего с твёрдым или жидким телом, можем записать:

dq = с_р (Т) dТ, (10)

где с_р (Т) – истинная удельная теплоёмкость твёрдого или жидкого вещества при постоянном давлении (известная функция), Дж/(кг·К).

Разделим обе части (10) на Т:

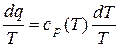. (11)

Очевидно, что интеграл от правой части (11) является непрерывной функцией температуры Т. Если обозначить эту функцию как s, то вместо (11) можем записать:

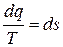, (12)

где s – некоторая непрерывная функция параметра состояния Т, то есть функция состояния, Дж/(кг·К).

Справедливость выражения (12) является доказательством существования энтропии у твёрдых и жидких тел в процессах их нагрева или охлаждения при постоянном давлении.