И для произвольного процесса, когда одновременно изменяются
и давление и объём (без индекса)
| Наименование теплоёмкости | Размер- ность | Обозначение теплоёмкостей | |||||
| Процесс при р = const | Процесс при υ = const | Процесс при р = var и υ = var**) | |||||
| средняя | истинная | средняя | истинная | средняя | истинная | ||
| Массовая | Дж/(кг · К) | сpm | ср | сυm | сυ | сm | с |
| Объёмная*) | Дж/(м3 · К) | с′pm | с′р | с′υm | с′υ | с′m | с′ |
| Мольная | Дж/(моль·К) | μсpm | μср | μсυm | μсυ | μсm | μс |
Примечания к таблице 1:
*)Для газов и газовых смесей удельная объёмная теплоёмкость обычно рассчитывается по формуле (1) для нормальных условий, то есть для объёма Vо, который этот газ (или газовая смесь) занимал бы при нормальных условиях (н.у.): ро = 101325 Па и tо = 0 °С. Один кубический метр газа, находящегося при н.у., называется нормальным метром кубическим и обозначается 1 нм3.
**) var – означает изменение величины (от латинского variare – изменяться).
5.2. Соотношения между удельными теплоёмкостями для газов и газовых смесей
При проведении расчётов, связанных с газами и газовыми смесями, всегда известной величиной является молярная масса газа μ (или кажущаяся молярная масса смеси μсм), кг/моль. Зная эту величину легко получить удобные формулы для пересчёта удельных теплоёмкостей одного типа в другой.
Для этого воспользуемся двумя следующими соотношениями. Из определения молярной массы вещества (это масса одного моля) следует, что:
М = μ · N, (3)
где М – масса вещества, кг; N – число молей вещества, моль; μ – молярная масса вещества, кг/моль.
Из следствия закона Авогадро известно, что 1 моль любого идеального газа занимает при н.у. объём 22,4 · 10–3 нм3/моль. Из этого следует, что плотность любого идеального газа при н.у. определяется соотношением:
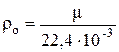 , (4)
, (4)
где ρо – плотность газа при н.у., кг/нм3; μ – молярная масса газа, кг/моль.
Воспользовавшись (4) можно вычислить объём, который газ (или газовая смесь) будет занимать при н.у.:
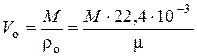 , (5)
, (5)
где Vо – объём, который газ будет занимать при н.у., нм3; М – масса газа, кг.
Из определений средних теплоёмкостей (10.1) и (1), (2) получаем путём очевидных преобразований:
 , м3/кг;
, м3/кг; 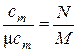 , моль/кг;
, моль/кг; 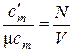 , моль/м3, (6)
, моль/м3, (6)
где М, V, N – масса, объём и число молей рассматриваемого вещества соответственно, кг, м3, моль.
Подставляя в правые части равенств (6) выражения, которые вытекают из (3) и (5), получаем формулы пересчёта теплоёмкостей для газов и газовых смесей, считая V = Vo (см. примечание табл. 1):
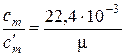 , нм3/кг;
, нм3/кг;
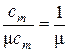 , моль/кг; (7)
, моль/кг; (7)
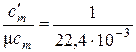 , нм3/моль.
, нм3/моль.
Повторив рассуждения для истинных теплоёмкостей, получаем аналогичные соотношения:
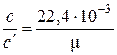 , нм3/кг;
, нм3/кг;
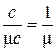 , моль/кг; (8)
, моль/кг; (8)
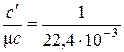 , нм3/моль.
, нм3/моль.
5.3. Расчёт значений средних теплоёмкостей
Рассчитать значение средней удельной теплоёмкости в некотором заданном интервале температур от t1 до t2 °С можно как по таблицам средних теплоёмкостей, так и по эмпирической формуле для истинной теплоёмкости.
Расчёт по таблицам ведётся на базе формулы определения средней теплоёмкости (см. раздел 10 формулу (10.2)):
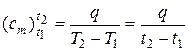 , (9)
, (9)
где 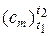 – средняя удельная теплоемкость в интервале температур от t1 до t2, Дж/(кг · К).
– средняя удельная теплоемкость в интервале температур от t1 до t2, Дж/(кг · К).
При этом значение теплоты q, которую необходимо подвести к 1 кг вещества чтобы нагреть его от t1 до t2 °С, определяется как разность двух теплот: теплоты 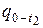 , которая затрачивается на нагрев от 0 до t2 °С и теплоты
, которая затрачивается на нагрев от 0 до t2 °С и теплоты 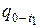 , которая затрачивается на нагрев от 0 до t1 °С:
, которая затрачивается на нагрев от 0 до t1 °С:
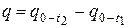 , Дж/кг. (10)
, Дж/кг. (10)
Для вычисления 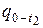 и
и 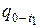 в таблицах выбираем значение средней теплоёмкости при температуре t2 – это средняя теплоёмкость в интервале температур от 0 до t2 °С:
в таблицах выбираем значение средней теплоёмкости при температуре t2 – это средняя теплоёмкость в интервале температур от 0 до t2 °С: 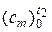 .
.
Соответственно будем иметь:
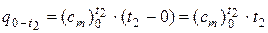 . (11)
. (11)
Аналогичным образом получаем:
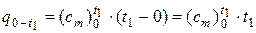 , (12)
, (12)
где 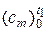 – табличные данные средней теплоёмкости при температуре t1, Дж/(кг·К).
– табличные данные средней теплоёмкости при температуре t1, Дж/(кг·К).
После подстановки (11) и (12) в (9) окончательно получаем формулу:
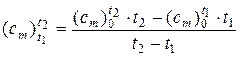 . (13)
. (13)
По формуле для истинной теплоёмкости значение средней теплоёмкости в интервале температур от t1 до t2 определяется как среднеинтегральное от функции с(t) в данном интервале температур.
Пусть эмпирическая формула для истинной удельной теплоёмкости имеет вид, аналогичный (10.6) (см. раздел 10):
с(Т) = a1 + a2 · t + a3 · t –2, (14)
где t – температура, oC; a1, a2 и a3 – известные для конкретного вещества коэффициенты.
Тогда формула для вычисления средней теплоёмкости в интервале температур от t1 до t2 имеет вид:
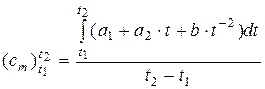 . (15)
. (15)
5.4. Теплоёмкость смеси идеальных газов
Рассмотрим идеальную газовую смесь, состоящую из n компонентов, масса которой М, кг. Для наглядности будем считать, что смесь нагревается в интервале температур равном одному градусу. Для нагрева такой смеси на один градус Цельсия (или Кельвина) необходимо температуру каждого из компонентов повысить на один градус.
Следовательно, к каждому компоненту необходимо подвести теплоту Qi, которая повысит температуру этого i-го компонента на один градус:
Qi = mi · ci · 1, Дж, (16)
где mi – масса i-го компонента, кг; ci – удельная массовая теплоёмкость i-го компонента, Дж/(кг·К).
Очевидно, что количество теплоты, необходимое для нагрева всей смеси на один градус Qсм, равно сумме теплот, необходимых для нагрева каждого компонента:
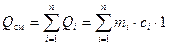 , Дж. (17)
, Дж. (17)
С другой стороны по определению удельной массовой теплоёмкости смеси ссм имеем:
Qсм = М · ссм · 1, Дж. (18)
Исходя из (17) и (18) можем записать:
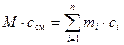 . (19)
. (19)
После деления обоих частей (19) на М получаем формулу для расчёта удельной массовой теплоёмкости смеси:
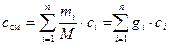 , Дж/(кг·К), (20)
, Дж/(кг·К), (20)
где gi – массовая доля компонента, кг/кг.
Так как химический состав смеси всегда задан, то значения массовых долей компонентов gi известны и по формуле (20) всегда можно рассчитать ссм.
Повторив рассуждения для объёмных и мольных удельных теплоёмкостей, можно легко получить аналогичные формулы:
с΄см = 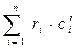 , (21)
, (21)
μссм =  , (22)
, (22)
где 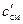 и μссм – удельные объёмная и мольная теплоёмкость смеси соответственно, Дж/(нм3·К), Дж/(моль·К); ri – объемная доля i-го компонента смеси; ki – мольная доля i-го компонента смеси; c'i и μci – удельные объёмная и мольная теплоемкость i-го компонента смеси, Дж/(нм3·К), Дж/(моль·К).
и μссм – удельные объёмная и мольная теплоёмкость смеси соответственно, Дж/(нм3·К), Дж/(моль·К); ri – объемная доля i-го компонента смеси; ki – мольная доля i-го компонента смеси; c'i и μci – удельные объёмная и мольная теплоемкость i-го компонента смеси, Дж/(нм3·К), Дж/(моль·К).
В формулах (21) и (22) следует учитывать, что объёмные доли численно равны мольным долям ri = ki (см. п. 3.2. Приложения 3).
Таким образом, при заданном химическом составе смеси значения ri известны и по формулам (21) и (22) всегда можно рассчитать 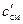 и μссм.
и μссм.
Следует отметить, что по формулам (20) – (22) могут быть рассчитаны средние и истинные теплоёмкости как при постоянном давлении, так и при постоянном объёме.
Дата добавления: 2015-03-19; просмотров: 1076;
