Логистическая модель прогнозирования
Экспоненциальная модель достаточно хорошо описывает процесс на этапах развития без влияния каких-либо мешающих внешних факторов, при этом темп роста (спада) остается неизменным. Однако во многих случаях на протяжении достаточно большого времени темп процесса не может считаться постоянным.
Рассмотрим модель процесса производства электроэнергии. Замечено, что темп роста производства электроэнергии непостоянен и с увеличением времени снижается. Это связано со многими факторами, среди которых главные: стремление к экономии электроэнергии, появление новых энергосберегающих технологий и ограничение энергетических ресурсов (рис. 5.14).

Рис. 5.14. Процесс выработки электроэнергии в логарифмических коор-
динатах
Для описания целого ряда массовых явлений, где одна группа факторов способствует развитию процесса, а другая, напротив, его тормозит, причем тем значительнее, чем дальше продвинулся процесс, используется так называемая логистическая (s-образная) кривая.
В случае, когда a = const, процесс производства электрической энергии выражается формулой (5.29) и в логарифмических координатах записывается как
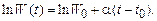 (5.31)
(5.31)
Возьмем производную от (5.31) по времени
 (5.32)
(5.32)
Если на всем рассматриваемом интервале времени производная (5.32) постоянна, то это экспоненциальная модель, в противном случае
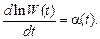 (5.33)
(5.33)
Так как со временем темп роста уменьшается, то можно предположить, что a(t) есть монотонно убывающая функция, и также использовать для нее экспоненциальную модель
 . (5.34)
. (5.34)
Логарифмируя выражение (5.34), получаем
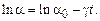 (5.35)
(5.35)
Таким образом, в логарифмических координатах (5.35) есть прямая линия (рис. 5.15).
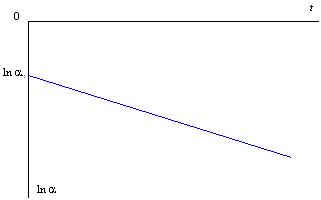
Рис. 5.15. Зависимость темпа роста процесса в лога-
рифмических координатах
Эта модель также могла быть получена из решения дифференциального уравнения (скорость уменьшения темпа a пропорциональна имеющейся величине)
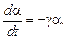 (5.36)
(5.36)
При начальных условиях t = t0 и a(t0) = a0 уравнение (5.36) имеет решение:
 (5.37)
(5.37)
Подставляя (5.37) в (5.32), будем иметь дифференциальное уравнение
 (5.38)
(5.38)
решить которое можно разделением переменных
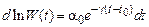 (5.39)
(5.39)
и интегрированием от момента времени t0 до момента t:
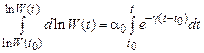 (5.40)
(5.40)
и
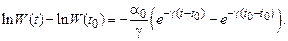 (5.41)
(5.41)
Имея в виду, что  , получаем
, получаем
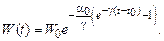 (5.42)
(5.42)
Полученное выражение (5.42) является логистической моделью процесса. С помощью этой модели достаточно хорошо описывается процесс годовой выработки электроэнергии во многих странах мира за последние десятилетия.
В СССР в 1960-е годы прирост электроэнергии составлял 5…6 % в год, в 80-е годы он снизился до 2…3 % в год. Аналогичная картина имеется и в некоторых других странах.
В тех случаях, когда зависимость ln a(t) не является прямой линией, логистическая модель не может быть использована.
Пример 1. Выполним прогноз годовой выработки электроэнергии по данным, приведенным в табл. 5.2, на 2000 и 2005 годы.
Таблица 5.2
Годовая выработка электроэнергии в СССР, млрд. кВт·ч
| Годы (ti) | |||||||
| Wi |
Для прогнозирования выберем экспоненциальную и логистическую модель
Для определения a в (5.29) найдем логарифмы Wi и найдем коэффициенты линейной функции 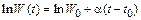 .
.
Таблица 5.3
Логарифмы Wi
| (ti – t0) | |||||||
| Ln Wi | 5,677 | 6,227 | 6,607 | 6,945 | 7,165 | 7,342 | 7,454 |
Здесь i = 0, 1, 2, …, n – 1 (n = 7).
Все расчеты и графические построения выполним в Mathcad.
Начальные значения:
Обозначения: Years – годы, W – годовое электропотребление, tn – первый год ретроспективы.
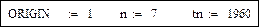
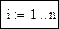
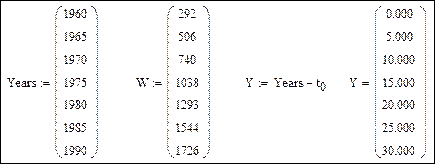
1. Экспоненциальная модель

В логарифмических координатах – линейная зависимость:
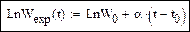
Экспоненциальная функция:
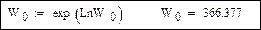
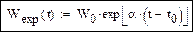
2. Логистическая модель 1
Для получения параметров логистической модели требуется дифференцирование функции ln W(t). Для функции, заданной дискретными значениями, получим n – 1 точек ее производной
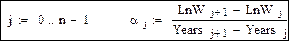
Прологарифмируем значения aj и запишем их в табл. 5.4.
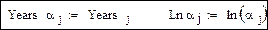
(значений a на единицу меньше, чем значений W)
Таблица 5.4
Значения a и логарифмы a
| (ti – t0) | ||||||
| ai | 0,11 | 0,076 | 0,068 | 0,044 | 0,035 | 0,022 |
| lnai | –2,208 | –2,577 | –2,693 | –3,125 | –3,339 | –3,804 |
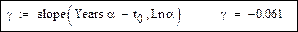
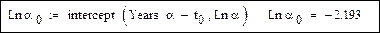

Построим график логарифма производной от энергии W (квадратиками обозначены дискретные значения из табл. 5.4). На графике показано, как ломаная кривая дискретных значений аппроксимируется прямой линией.
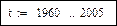
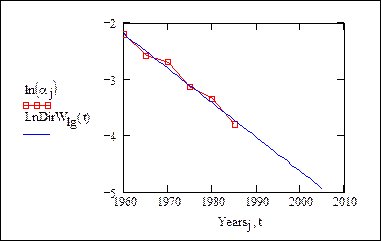
Запишем функции для логистической модели:
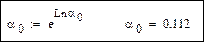
С учетом знака минус g:

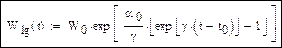
Построим графики логарифмов экспоненциальной и логистической модели:
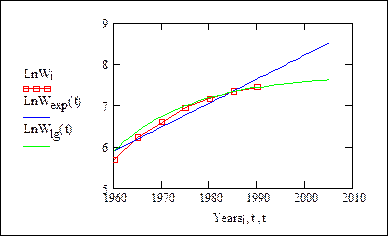
На графике видно, что логистическая зависимость дает более точные совпадения с экспериментальными данными.
Построим графики самих математических моделей:

В системе Mathcad имеются специальные функции проведения регрессии для некоторых наиболее распространенных моделей, в том числе для экспоненциальной и логистической модели:
expfit(vx, vy, vg) – возвращает вектор, содержащий коэффициенты (a, b и c) аппроксимирующего выражения экспоненциальной модели вида 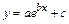 , график которого лучшим образом приближается к точкам, координаты которых хранятся в векторах vx и vy (вектор vg содержит первое приближение к решению);
, график которого лучшим образом приближается к точкам, координаты которых хранятся в векторах vx и vy (вектор vg содержит первое приближение к решению);
lgsfit(vx, vy, vg) – возвращает вектор, содержащий коэффициенты (a, b и c) аппроксимирующего выражения логистической модели вида 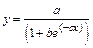 , график которого лучшим образом приближается к точкам, координаты которых хранятся в векторах vx и vy (вектор vg содержит первое приближение к решению).
, график которого лучшим образом приближается к точкам, координаты которых хранятся в векторах vx и vy (вектор vg содержит первое приближение к решению).
Выполним моделирование по указанным функциям.
Экспоненциальная модель 2


Логистическая модель 2

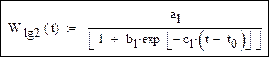
Графические построения по обеим моделям

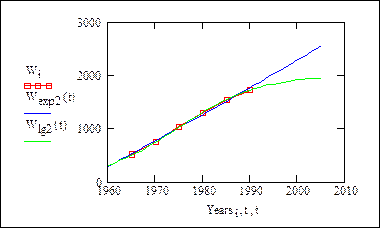
В системе Mathcad есть функция линейного алгебраического предсказывания predict. Она применяется для гладких и периодических функций и является разновидностью экстраполяции.
predict(v, m, n) – возвращает n предсказанных значений, основанных на m последовательных значениях вектора данных v. v – представляет собой вектор равномерно расположенных данных (через равные интервалы по аргументу).
Функция predict использует последние m исходных значений данных, чтобы вычислить коэффициенты предсказания. Как только это сделано, она использует последние m точек, чтобы предсказать координаты m + 1-й точки, фактически создавая скользящее окно шириной в m точек.
Выполним прогноз выработки электроэнергии с помощью этой функции:
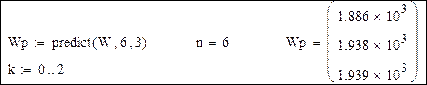
Графическая сравнительная иллюстрация моделей из инструментальных средств Mathcad.

Оценка погрешностей моделей и численные значения прогноза на 2000 и 2005 годы.

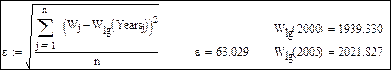
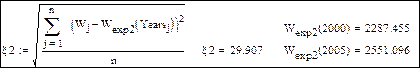
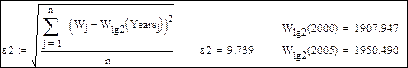
Дата добавления: 2015-03-19; просмотров: 1801;
