Случайные процессы

Функция X(t) называется случайной, если ее значение при любом аргументе t является случайной величиной. Случайные функции времени называют случайными процессами.

Реализацией случайной функции X(t) (выборочной функцией) называется конкретный вид, который она принимает в результате опыта. Реализация случайного процесса может рассматриваться как элемент множества возможных физических реализаций случайного процесса (рис. 5.8). Совокупность реализаций случайного процесса называется ансамблем реализаций. Совокупность значений реализаций в фиксированный момент времени (выборка случайных значений) называется сечением случайного процесса.

Рис. 5.8. Реализации случайного процесса

В любом сечении случайный процесс есть случайная величина.

Математическое ожидание случайного процесса есть функция времени

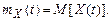(5.10)

Второй центральный момент для двух сечений случайного процесса называется ковариационной функцией

(5.11)

где 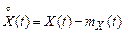– центрированный случайный процесс.

При t = t′ ковариационная функция равна дисперсии случайного процесса

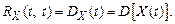(5.12)

Математическое ожидание и ковариационная функция случайного процесса могут быть найдены по реализациям случайного процесса – осреднением по реализациям:

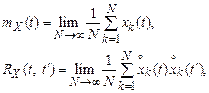(5.13)

где N – число реализаций случайного процесса.

Если математическое ожидание и ковариационная функция не зависят от времени t, то процесс является стационарным:

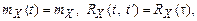(5.14)

где τ = t′ – t. В (5.14) ковариационная функция зависит только от величины τ, а не от места его расположения на оси времени (рис. 5.9).

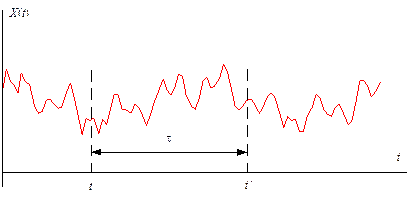
Рис. 5.9. Время между двумя сечениями случайного процесса

Возможный вид ковариационной функции показан на рис. 5.10.

Во многих случаях используется нормированная ковариационная (или корреляционная) функция. Для стационарного случайного процесса

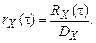(5.15)

Величина корреляционной функции |r_X(t)| ≤ 1.

Возможно осреднение по времени отдельных выборочных функций (реализаций). Для k-й выборочной функции имеем:

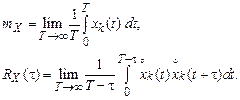(5.16)

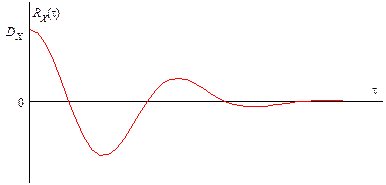
Рис.5.10. Ковариационная функция случайного процесса

Если случайный процесс X(t) стационарен и характеристики m_X и R_X(τ) одинаковы для различных выборочных функций, то такой процесс называют эргодическим.

Эргодические процессы представляют важный класс случайных процессов.

Нестационарными случайными процессами являются все случайные процессы, не обладающие свойствами стационарности. Эти процессы сложны в исследованиях, и зачастую в задачах по анализу их разбивают на интервалы стационарности или приближенно аппроксимируют стационарными процессами.