Экспоненциальная модель прогнозирования
Во многих случаях в качестве математического описания физических процессов используется экспоненциальная функция. Рассмотрим такую модель на примере процесса распада радиоактивного элемента.
Известно, что скорость распада любого радиоактивного элемента прямо пропорциональна наличной его массе:
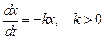. (5.17)
Знак минус указывает на убывание массы.
Разделим переменные в дифференциальном уравнении (5.17):
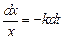(5.18)
и после интегрирования получим
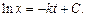(5.19)
При t = 0 из (5.19) будем иметь C = lnx0, где x0 – количество массы в начальный момент времени, тогда
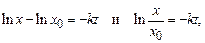(5.20)
откуда
, (5.21)
где k – константа, которая может быть определена экспериментальным путем.
Пусть за время Dt = t – t0 распалось a % радиоактивного элемента, тогда остаток (рис. 5.14).
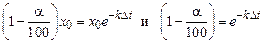. (5.22)
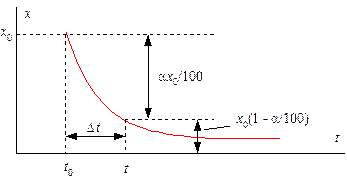
Рис. 5.14. Определение параметра модели распада радиоак-
тивного элемента
Логарифмируя полученное выражение и выражая коэффициент k, получим
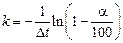. (5.23)
Для элемента радия k = 0,00044 1/год.
Во многих случаях экспоненциальная модель зарекомендовала себя очень хорошо как в случае убывания некоторой субстанции, так и для роста субстанции. В общем случае модель формулируется следующим образом: скорость изменения некоторой субстанции (роста, спада) пропорциональна уже имеющемуся количеству. Так, например, скорость увеличения выработанной электрической энергии
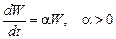, (5.24)
т. е. прирост показателя в единицу времени пропорционален уже имеющемуся количеству (достигнутому уровню) с неизменным коэффициентом пропорциональности a = const.
В логарифмических координатах зависимость ln W(t) – прямая линия.
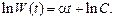(5.25)
В случае начала отсчета t = t0 (t0 ≠ 0), W = W0 и
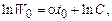(5.26)
откуда
(5.27)
и
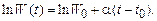(5.28)
Окончательно получаем модель
(5.29)
В некоторых случаях оказывается более удобной модель с постоянным коэффициентом b:
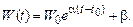(5.30)
Дата добавления: 2015-03-19; просмотров: 1137;