Лекція №33

Навчальні питання:

1. Пластична та пружна деформація металу.

2. Наклеп металу.

Навчальне питання 1. Пластична та пружна деформація металу.

Під дією прикладених ззовні сил метал, як і будь-яке тверде тіло, змінює свою форму та розміри. їх зміна називається деформацією.

При малих ступенях деформації діє відомий закон Гука:

σ=ԑЕ

де σ- напруження; ԑ- відносна деформація; Е-модуль пружності.

Метал при цьому деформується пружно: атоми зміщуються з поло­жень рівноваги у кристалічній гратці (рис. 3.1), відстані між ними змінюються, в результаті чого порушується баланс сил притягання а та електростатичного відштовхування Ь і виникає рівнодіюча сила с, яка намагається повернути атом у положення рівноваги п. Сума вказаних сил, які діють на усі зміщені атоми, розташовані на одиниці площі поперечного перерізу металу, називається напруженням:

σ=Р/S,

де σ- напруження; Р-зовнішнє навантаження; S- площа поперечного перерізу.

Поки не перевищена границя пружності σ_пруж, після зняття зовнішнього навантаження кожен атом повертається у положення рівноваги, а пружні деформації га напруження обертаються на нуль. Структура металу при цьому не змінюється.

Слід зауважити, що визначення границі пружності σ_пруж досить тривале і трудомістке, тому на практиці замість неї визначають або границю пропорційності σ_пц, або границю текучості, фізичну σ_т чи умовну σ₀₂- Але σ_пруж менша від усіх них.

Коли напруження в металі перевищать границю пружності, закон Гука стає непридатним, виникає необоротна, або залишкова дефор­мація, яка зростає зі збільшенням навантаження аж до руйнування металу. Пружна деформація при цьому зберігається і навіть збільшу­ється. Процес, який спричиняє залишкові зміни у металі, називається пластичною деформацією.

Ні чисте всебічне розтягання, ні стиснення не дають залишкової деформації. Єдиним типом навантаження, здатним спричинити залиш­кове зміщення атомів щодо один одного без порушення зв'язку між ними, є навантаження зсуву. Зсувна деформація полягає у організо­ваному переміщенні окремих частин кристала (ковзання) або групи його атомних площин (двійникування), в результаті якого кристал і все тіло витягається уздовж напрямку дії зовнішньої сили при відповід­ному зменшенні поперечних розмірів.

Дотичні напруження у кристалі.Не варто думати, що залишкова деформація може бути викликана виключно зсувними навантаженнями, а не розтягувальними або стис­кувальними. Але в цих випадках ефективною є лише та частина зовнішнього навантаження, та її складова, що відповідає силам зсуву і створює у кристалі дотичні напруження.

Будь-яке зовнішнє навантаження Р може бути розкладено (рис. 3.2) на дві складові: нормальну N та дотичну К. Складова N перпенди­кулярна площині ковзання, вона створює нормальні напруження і спричинює пружну деформацію. Складова К лежить у площині ковзан­ня і є силою зсуву, яка створює дотичні напруження та спричинює пластичну деформацію.

Якщо позначити через А площу поперечного перерізу кристала, то і площа площини ковзання S:

S=А/соsѲ,

де Ѳ - кут між напрямком зовнішнього навантаження та нормаллю до площини ковзання.

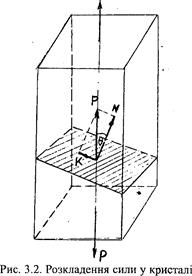
Водночас складова К сили Р:

К=РsinѲ.

Тоді дотичне напруження σ:

σ=К/S=Р/AsinѲcosѲ-Р/2Аsin2Ѳ.

Звідси випливає, що дотичне напруження σ=0, коли sin2 Ѳ=0, тобто при Ѳ=0° або Ѳ=90°.

Максимальне ж дотичне напруження становитиме:

σ_max=P/2A=0,5σ_{розтягн}(σ_стисн)

Воно досягає свою максимуму при sin2Ѳ=1, тобто коли Ѳ=45°. Отже, при розтяганні та стисненні дотичні напруження дорівню­ють нулю у площинах, паралельних та перпендикулярних осі розтя­гання (стиснення), та досягають максимуму, що дорівнює половині величини напружень розтягання чи стиснення у площинах, розташо­ваних під кутом 45° до осі розтягання (стиснення). Такі площини нази­ваються площинами найлегшого зсуву.

Джерела Франка-Ріда.Джерело Франка-Ріда являє собою дислокацію, один або обидва кінці якої закріплені іншими, нерухомими дислокаціями, розташо­ваними у площинах, де ковзання неможливе, наприклад, у площинах з великими кристалографічними індексами. Така дислокація здатна переміщуватися за рахунок зміни положення її іншого кінця або центральної частини. У результаті цього вона може рухатися уздовж площини ковзання під дією зовнішнього навантаження.

При збільшенні останнього дислокація DD', закріплена на обох кінцях (рис. 3.4), спочатку вигинається у своїй центральній частині, потім перетворюється на дві з'єднані півспіралі. При їх зближенні відбувається анігіляція, оскільки ці частини півспіралей є дислокаціями протилежних знаків. У результаті утворюється замкнений дислока­ційний контур, всередині якого відтворюється первісна дислокація. Якщо зовнішнє навантаження продовжує зростати, джерело Франка - Ріда генерує другий дислокаційний контур, потім - третій, четвертий і т.д., подібно до утворення мильних бульок на кінці трубки.

Замкнений криволінійний дислокаційний контур можна розкласти на компоненти - лінійні та гвинтові дислокації обох знаків (рис. 3.5). Під дією зростаючого навантаження цей замкнений контур буде розширюваатися, його межі будуть розходитися в усі боки. Просування контуру крізь кристал призведе до зсуву на одну міжплощинну відстань, але лише у напрямку дії навантаження. Хоча сторони квадра­та розходятся на всі боки, зсув, спричинений їх рухом, відбувається лише уздовж лінії дії вектора навантаження.

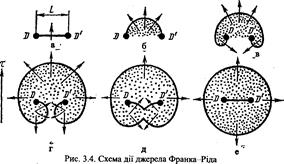
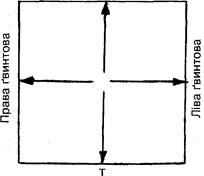
Рис. 3.5. Апроксимація дислокаційного контуру

Навчальне питання 2. Наклеп металу.

Пластична деформація здійснюється шляхом естафетного перемі­щення дислокацій. У ньому беруть участь як дислокації, що уже були в металі раніше, так і ті, які виникли у процесі пластичної деформації. Тому їх густина збільшується з 10⁵...10⁸ до 10¹⁰...10¹² на 1 см². З цим пов'язане зміцнення металу у процесі пластичної деформації, яке називається наклепом.

Наклеп є наслідком того, що просування дислокації у площині ковзання поступово утруднюється в результаті взаємодії з іншими дислокаціями, що рухаються у площинах, які перерізають цю площину. Поникає так звана ґратка дислокацій та поля локальних напружень, які оточують дислокації.

Для подальшого росту деформації потрібно збільшувати зовнішнє навантаження та створені ним дотичні напруження. Отже, метал у процесі пластичної деформації стає міцнишим - це і є наклеп. Ха­рактерно, що зміцнюються не лише уже діючі площини ковзання, а й паралельні їм на певній відстані від діючої, тобто в остаточному підсумку - увесь кристал.

У процесі пластичної деформації дислокації також застряють біля річних перешкод (вакансій, меж зерен тощо), що призводить до утворення (рис. 3.6) їх горизонтальних угруповань (стінок). Одноймен­ні дислокації, як відомо, відштовхуються одна від одної, утворюючи поле напружень. При певній його величині джерело Франка-Ріда перестає працювати, і деформація припиняється. При збільшенні зовнішнього навантаження знову починає діяти джерело Франка-Ріда,

деформація поновлюється і т.д. до насичення або руйнування металу.

Отже, залежність міцності металу від густини дислокацій у ньому має досить складний характер (рис. 3.7). Максимальну або теоретичну міцність мають абсолютно бездефектні кристали. Такі кристали мо­жуть бути одержані й на практиці шляхом спрямованої кристалізації на відповідно підібраній підкладці. За своїм розташуванням на ній ці кристали одержали назву вусів. На жаль, їх розміри (діаметр 2...10 мкм, довжина декілька міліметрів) виключають їх практичне застосування.

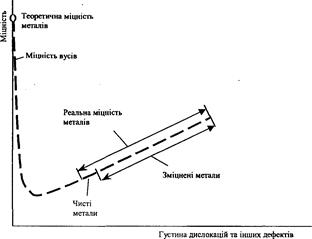
Рис. 3.7. Міцність кристала залежно від викривлень гратки (за І. Одінгом)

З появою дислокацій та збільшенням їх густини міцність металу швидко зменшується і досягає мінімуму, що дорівнює експерименталь­ним її значенням для металів технічної чистоти, де густина дислокацій становить 10⁷...10⁸ на 1 см².

Подальше збільшення густини дислокацій приводить до суттєвого, у декілька разів, збільшення міцності металу. Крім наклепу, цього можна досягти за допомогою термічної обробки та легування металу.

Двійникування.Вище було розглянуто найпоширенішій механізм пластичної деформації - ковзання, іншим її механізмом є двійникування. Це - своєрідна систематична форма ковзання, яка приводить до зміни орієнтації частини кристала (двійникової області) щодо решти об'єму того ж кристала. Розташування атомів у двійниковій області (рис. 3.8) є дзеркальним відображенням (щодо площини двійникування) структу­ри, яка існує в іншій частині цього кристала. Фізично такий поворот, звичайно, неможливий, тобто двійникування є своєрідною видозміною ковзання.

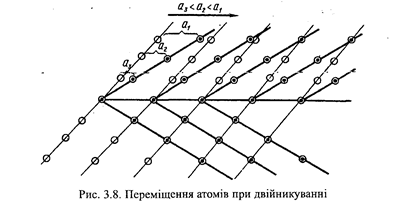
Але при ковзанні сусідні атомні площини зміщуються на відстані, що кратні цілому числу міжатомних відстаней б, а при двійникуванні - часткам цієї відстані, які збільшуються при віддаленні від площини

двійникування {х₁<х₂^< <х₃<...).

У мікроструктурі деформованого металу двійник обмежений прямими лініями, має іншу травимість, ніж решта кристала, і не пере­пікає межу зерна. На нетравленому мікрошліфі двійників не видно, проте видно смуги ковзання. Полірування мікрошліфа усуває смуги ковзання, а двійники залишаються.

Смугою (пачкою) ковзання називається лінія мікроскопічних розмірів, розташована на вільній поверхні металу. Вона є слідом пере­різу активної площини ковзання (або групи таких площин) з вільною поверхнею металу (площиною мікрошліфа). Г. Хайденрайх довів, що товщина смуги ковзання становить близько 100 міжплощинних відста­ней. Це означає, що навіть при дуже великій деформації активізується та використовується не більше 1 % можливих площин ковзання. У кожній системі площин активні площини відокремлені відстанями, не меншими ніж 100 міжатомних. Саме такі відстані відокремлюють сусідні джерела Франка-Ріда.

Дислокаційний механізм ковзання.Раніше вважалося, що під дією дотичних напружень одна поло­вина кристала водночас і одразу зміщується щодо іншої його половини на одну або інше ціле число міжплощинних відстаней. Коли ж підраху­вали потрібні для цього зусилля, або, інакше кажучи, теоретичну міцність, виявилося, що остання на декілька порядків величини більша за експериментально визначену міцність того ж самого металу. Наприклад, теоретична міцність заліза становить 11000, а експери­ментальна - усього 29 МПа.

Для усунення цього протиріччя Д. Тейлор, Е. Орован і М. Поляні запропонували скористатися теорією дислокацій. На їхню думку, ковзання є результатом утворення та переміщення дислокацій. Спрощена схема цього процесу подана на рис. 3.3.

Під дією зовнішнього навантаження півплощина l починає руха­тися вправо і врешті-решт виходить зі зчеплення з півплощиною l'. При подальшому русі півплощина 1 входить у зчеплення з півплощиною 2^', а верхня частина останньої перетворюється на екстраплощину, тобто утворюється позитивна лінійна дислокація. Далі ця дислокація, подібно до естафетної палички, переходить з однієї атомної площини в сусідню, поки не вийде на межу зерна, де й зникає. Результатом її утворення та руху є зсув однієї половини кристала щодо іншої на одну міжплощинну відстань, як це передбачалося і класичною теорією ковзання. Але для утворення і руху дислокації потрібні зовсім невеликі зовнішні навантаження та створені ними напруження, які дорівнюють експериментальній міцності матеріалу.

Інформаційні джерела:

1. Технологія конструкційних матеріалів./За ред. А.М. Сологуба. - К.: Вища школа, 1993 –

300 с.

2. Большаков В.І., Береза О.Ю., Харченко В.І. Прикладне матеріалознавство: Підручник. Дніпропетровськ: РВА „Дніпро VAL”.2000 – 290 с.

3. Технология конструкционних материалов. /Г.А. Прейс, М.А. Сологуб, И.А. Рожнецкий/ - К.: Вища школа 1991 – 391 с.

4. Дальский А.М. и др. Технология конструкционных материалов, М.: Машиностроение. 1990 - 351 с.