Пример отчета по лабораторной работе. 11.8.1 Метод обработки результатов по методу противопоставления
11.8.1 Метод обработки результатов по методу противопоставления
Будем взвешивать навеску порошка сульфата меди (CuSO4) массой 10 г и плотностью 3,603 г/см3; измерение проводим три раза.
Результат измерения массы изделия вычислим по формуле (11.1):
аНгi = 10 г;
аВгi1 = 0,00040 г;
аВгi2 = 0,00020 г;
аВгi3 = 0,00055 г;
n = 3
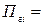 - 0,00007 г;
- 0,00007 г;
Рассчитаем значение поправки:
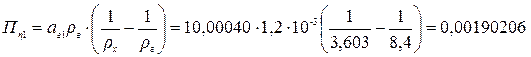 г;
г;
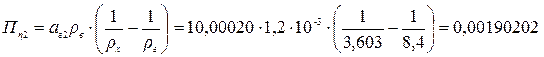 г;
г;
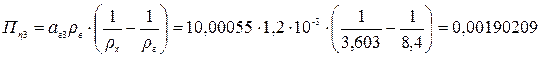 г;
г;
(rх=3,603 г/см3; rг=8,4 г/см3 для гирь из латуни; rв =1,2*10-3 г/см3)
 0,00040 - 0,00007+0,00190206 = 10,00223206 г;
0,00040 - 0,00007+0,00190206 = 10,00223206 г;
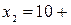 0,00020 - 0,00007+0,00190202 = 10,00203202 г;
0,00020 - 0,00007+0,00190202 = 10,00203202 г;
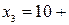 0,00055 - 0,00007+0,00190209= 10,00238209 г;
0,00055 - 0,00007+0,00190209= 10,00238209 г;
Найдем среднее арифметическое значение:
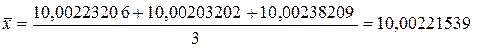 г;
г;
Погрешность из-за неточности определения массы накладной гири определим по формуле (11.3):
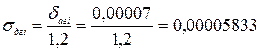 г;
г;
Погрешность из-за неравноплечести коромысла определим по формуле (11.4):
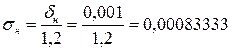 г;
г;
Погрешность включений встроенных гирь определим по формуле (11.5):
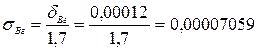 г;
г;
Случайную составляющую погрешности определим по формуле (11.6):
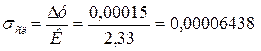 г;
г;
Погрешность измерения массы по шкале определим по формуле (11.7):
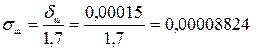 г;
г;
Погрешность считывания определим по формуле (11.8):
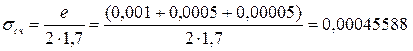 г;
г;
Методическую погрешность определим по формуле (11.11):
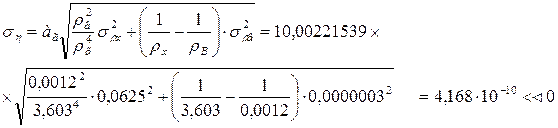
Из-за малости полученной величины в расчете мы не учитываем
где rв =1,2*10-3 г/см3
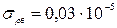 г/см3
г/см3
СКО погрешности определения поправки из-за отклонения плотности груза от её номинального значения определим по формуле (11.12):
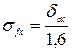
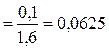 г, (
г, ( 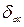 рекомендуется принимать 0,1 г/см3)
рекомендуется принимать 0,1 г/см3)
Математическое ожидание погрешности определения поправки определим по формуле (11.10):
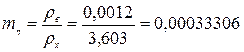 г;
г;
Границы погрешности измерения массы изделия при вероятности 0,95 оценим по формуле (11.2):
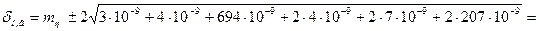
Δн.е. = 0,00033306 ± 0,0674689 г;
Запишем результат измерения:
9,93508 г; < 10,00222 г; < 10,07002 г;
Вывод по проведенной лабораторной работе:
Вывод студент формулирует самостоятельно, изучив ход взвешивания, рассуждений и результаты погрешностей, исходя из сравнения по методикам обработки результатов наблюдений.
11.8.2 Метод обработки результатов измерений по РМГ 29
Будем взвешивать навеску порошка сульфата меди (CuSO4) массой 10 г и плотностью 3,603 г/см3; измерение проводим три раза.
Результат измерения массы изделия вычислим по формуле (11.1):
аНгi =10 г;
аВгi1 = 0,00040 г;
аВгi2 = 0,00020 г;
аВгi3 = 0,00055 г;
n = 3
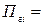 - 0,00007 г;
- 0,00007 г;
Вычисляем значение поправки:
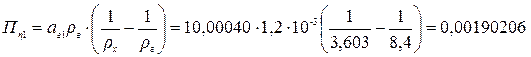 г;
г;
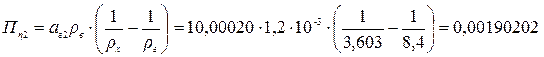 г;
г;
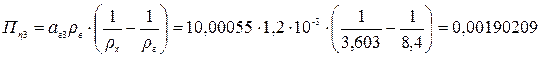 г;
г;
(rх=3,603 г/см3; rг=8,4 г/см3 для гирь из латуни; rв =1,2*10-3 г/см3)
 0,00040 - 0,00007+0,00190206 = 10,00223206 г
0,00040 - 0,00007+0,00190206 = 10,00223206 г
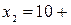 0,00020 - 0,00007+0,00190202 = 10,00203202 г
0,00020 - 0,00007+0,00190202 = 10,00203202 г
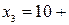 0,00055 - 0,00007+0,00190209= 10,00238209 г
0,00055 - 0,00007+0,00190209= 10,00238209 г
Находим среднее арифметическое:
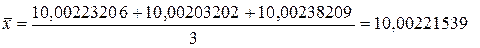 г
г
Найдем СКО:
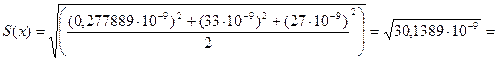
S(X) = 0,00549 г;
Определяем неисключенную систематическую погрешность:
Θ(Р) = ±|0,00025+0,00012+0,00015| = 0,00052 г;
Находим значение Θ(Ρ)/S(x):
Θ(Ρ)/S(x) = 0,00052/0,00549 = 0,095
0,095 < 0,8 – доверительную границу погрешности результата измерений вычисляют по формуле (11.19):
Δ(Р) = 1,414 · 0,00549 = 0,00776
Запишем результат измерения:
А = 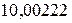 ± 0,00776 г
± 0,00776 г
Вывод по проведенной лабораторной работе:
Вывод студент формулирует самостоятельно, изучив ход взвешивания, рассуждений и результаты погрешностей, исходя из сравнения по методикам обработки результатов наблюдений.
11.8 Варианты выполнения лабораторной работы:
| № по списку гр. | Масса г; | № по списку гр. | Масса г; |
| 7,5 | 14,0 | ||
| 8,0 | 14,5 | ||
| 8,7 | 15,0 | ||
| 8,9 | 15,6 | ||
| 9,3 | 15,85 | ||
| 9,7 | 16,45 | ||
| 10,0 | 16,8 | ||
| 10,5 | 17,0 | ||
| 10,8 | 17,56 | ||
| 11,2 | 17,95 | ||
| 11,5 | 18,36 | ||
| 11,8 | 18,65 | ||
| 12,4 | 19,0 | ||
| 12,75 | 19,5 | ||
| 13,0 | 20,0 | ||
| 13,5 | 20,56 |
Вопросы для самоконтроля
11.9.1 Расскажите, что знаете о классификации методов измерения массы.
11.9.2 Какие Вы знаете средства измерения массы?
11.9.3 Лабораторные весы: классификация по буквенно-цифровой индексации.
11.9.4 Принцип действия весов ВЛР-200.
11.9.5 Поправка на действие выталкивающей силы.
11.9.6 Причина возникновения погрешности считывания, погрешности неравноплечести коромысла.
11.9.7 Перечислите операции, выполняемые при статистической обработке результатов наблюдений.
11.9.8 Как определяется результат неисключенной систематической погрешности?
11.9.9 Причины возникновения случайных погрешностей.
11.9.10 Доверительная граница соотношения погрешностей результата измерений при условии 0,8 < 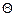 (Ρ)/S(x) < 8.
(Ρ)/S(x) < 8.
Дата добавления: 2015-01-13; просмотров: 2405;
