Диагностический алгоритм для оценки технического состояния при усталостном процессе
При прогнозировании ресурса следует исходить из того, что процесс изменения напряжений в деталях машин не может быть стационарным в принципе, поскольку, как минимум, этому способствуют неровности взаимодействующих поверхностей. В результате из-за влияния многих факторов процесс нагружения является случайным. Такие процессы, описываемые корреляционной функцией или энергетическим спектром, недифференцируемы, в результате чего невозможен их структурный анализ и усложнен расчет на сопротивление усталости [14]. Дело в том, что хотя методологически случайный процесс относительно легко может быть смоделирован и воспроизведен посредством четырех параметров (матожидание нагрузки и ее СКО, эффективная частота и коэффициент широкополосности), но сложно получить и экспериментально подтвердить модель сопротивления усталости при вариации этих параметров. Поэтому необходима дополнительная обработка реального процесса, если речь идет об управлении безопасностью.
При чисто случайном нагружении периодичность плохо прослеживается, а это не характерно для технологического оборудования. Установившаяся технология выполнения работ делает процесс нагружения псевдослучайным, а устоявшаяся частота приводов механизмов характеризует эксплуатационный процесс как периодически - случайный. Поэтому их можно схематизировать формализованными блоками, отражающими историю нагружения.
Нагруженность объектов металлургического оборудования представляется итоговым спектром, который формируется методом синтеза. Основа его состоит в нахождении технологической операции, при которой процесс нагружения будет эргодическим. Далее на основании статистических исследований повторяемости режимов (организационный фактор) определяется закон распределения нагрузок (рис. 5.1). Подобные итоговые спектры имеют высокий коэффициент вариации нагрузок (νQ≈ 0.5 и более), что не дает возможности уточнять расчет и повышать безопасность при эксплуатации. Высокий коэффициент вариации обусловлен многорежимностю эксплуатации. Вариация нагрузок по амплитуде в течение одного режима даже с учетом динамических явлений, как правило, составляет νQi = 0,05 ... 0,15. Незначительно меняется и частота нагружений [15].
| Q |
| t |
| C1 |
| C2 |
| Ci |
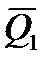
|
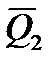
|
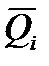
|
| VQ1 |
| VQ2 |
| VQi |
| Q |
| C |
| C1 |
| C2 |
| Ci |
| … |
| VQ |
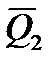
|
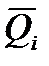
|
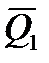
|


а б
Рис. 5.1. Формирование спектра нагрузок (б) путем синтеза режимов нагружения Q(t) (а), которые наблюдаются при обработке машиной различных сортаментов металлопродукции, с повторяемостью Ci и средней нагрузкой 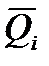 .
.
Известны системы мониторинга, которые классифицируют результаты измерений нагрузок, объединяя их в спектры [15,16] и рассчитывая значение итогового коэффициента вариации νQ . Его изменение говорит либо об изменении вида работ (технологии), либо об изменении технического состояния (износе) оборудования. Таким образом, спектр нагрузок выступает в качестве диагностического признака, который имеет эталонные показатели, что дает возможность судить о ТС объекта. Невозможность определениякритических (предельных) показателей спектра не дает шансов использовать его в качестве диагностического параметра при прогнозе ресурса. Для этой цели нет смысла обрабатывать временную реализацию нагрузок в виде спектра. Следует установить параметры такого первичного случайного процесса, который отражает естественную эксплуатационную нестационарность нагрузки. Под получаемую во время эксплуатации информацию о процессе нагружения Q(t) необходимо построить диагностический алгоритм, основанный на адекватных моделях сопротивления усталости.
Для этой цели пригодна модель ресурсного типа, где циклическая нагруженность характеризуется повреждающим действием, ведущим к накоплению повреждений, которые выступают в роли диагностического параметра. К моменту оценки ресурса i после nΣi числа циклов наработки степень исчерпания ресурса материала в конструкции, характеризуемая накопленным повреждением, составляет 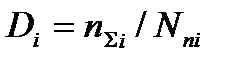 (рис. 5.2). величина
(рис. 5.2). величина 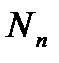 , фактически, представляет долговечность при нестационарном нагружении, т.е. общее число циклов разного уровня, которое выдержал бы объект, если дальнейший режим нагружения будет происходить с прежней скоростью исчерпания ресурса VDi (рис. 5.2):
, фактически, представляет долговечность при нестационарном нагружении, т.е. общее число циклов разного уровня, которое выдержал бы объект, если дальнейший режим нагружения будет происходить с прежней скоростью исчерпания ресурса VDi (рис. 5.2):
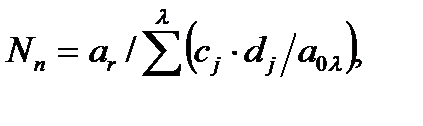 (5.1)
(5.1)
где λ- число блоков нагружения, которые состоят из j ступеней,
cj=nj/n0 – относительное число циклов нагружения j-ой ступени в общем числе циклов нагружения блока,
dj=1/Nj – элементарное (за один цикл) повреждение, являющееся обратной величиной к долговечности при стационарном нагружении N,
аr и a0λ – межблочное (устанавливается для всего процесса) и внутриблочное (устанавливается для блока, имеющего форму λ) повреждения, характеризующие интенсивность их накопления.
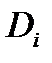 , будет:
, будет:
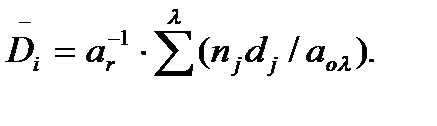 (5.2)
(5.2)
Для определения исходного или проектного ресурса 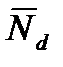 обычно принимают
обычно принимают 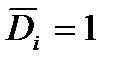 (рис. 5.2), а нагружение представляется в виде спектра.
(рис. 5.2), а нагружение представляется в виде спектра.
При диагностировании оборудования путем мониторинга нагруженности его узлов отслеживается фактор истории нагружения (характера чередования циклов, что влияет на интенсивность накопления повреждений). В результате этого, применительно к диагностическим алгоритмам и моделям сопротивления усталости появляются следующие возможности.
| D |
| [D]i |
| [D]1 |
| NnR1 |
| NnRi |
| NnR2 |
| [D]2 |
| N |
| arctgVD1 |
| arctgVD2 |
| arctgVDi |
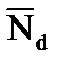
|
| nΣ1 |
| nΣ2 |
| nΣi |
Рис.5.2. Интерпретация пошаговой переоценки ресурса по кинетике накопления усталостных повреждений (исчерпанию ресурса)
1. Идентифицируется деградационная модель - из широкого веера графиков накопления повреждений (рис. 5.1) выбирается конкретная реализация процесса. Данное положение из теории диагностики является основой индивидуального прогнозирования и позволяет повысить безопасность за счет уточнения ресурса.
2. Подобная идентификация связана с применением фактического режима нагружения, при котором конкретизируются величины внутри- и межблочного повреждений a0 и аr, что позволяет повысить безопасность за счет более достоверной оценки ресурса. (Здесь мы не рассматриваем отклонения в определении ресурса, связанные с ошибками при оценке величин dj и cj на проектной стадии. В этом аспекте также имеется резерв повышения безопасности.)
На практике мониторинг работоспособности механических систем возможен двумя способами:
1) путем контроля (сполошного или периодического) процесса нагружения Q(t),
2) путем контроля процесса наработки nΣ(t) в числах циклов.
Таким образом, мы имеем два диагностических признака.
Первый способ более информативен, обеспечивает более достоверное прогнозирование, но требует наличия специальных встроенных измерительных систем. Второй способ этого не требует, но предполагает проведение исследований нагруженности, по результатам которых разрабатывается формализованный блок с вероятностными значениями параметров. Его использование возможно, практически, для любых механических систем. От применяемого способа (диагностического признака) зависит диагностический алгоритм оценки накопленного повреждения (диагностического параметра).
В его основе заложен закон суммирования повреждений. В данных моделях, как видно, используется корректированный закон линейного суммирования. Данный вопрос является весьма неоднозначным в теории сопротивления усталости и для применяемых моделей определяется формой схематизированного (или реального) блока. Следовательно, неоднозначно решается вопрос об объеме (числе циклов) блока нагружения. Форма блока, в первую очередь, определяется последовательностью технологических операций. Этот фактор из случайного может транформироваться в детерминированный, что сужает поле возможных реализаций деградационного процесса. Скажем, во время прокатки заготовки в элементах привода валков наблюдаются динамические колебания и возрастание крутящего момента при захвате металла. Затем наблюдается установившийся процесс с несущественным циклированием, после чего при выпуске металла вновь появляется колебательный процесс с повышенной амплитудой (рис. 5.2, а). Эти факты дают право сформировать типовую историю нагружения в виде трехступенчатого блока, отвечающего прокатке одной заготовки. Однако, вряд ли такой подход будет продуктивен, поскольку огромное число прокатываемых заготовок дает высокое перемешивание реализаций нагружения, при котором величины a0 и аr стремятся к единице. Практика опровергает это положение. И если необходимо повысить степень выработки ресурса при эксплуатации, стоит отследить возможное отклонение величин a0 и аr от единицы.
Считается, что фактор истории нагружения значим, когда итоговая долговечность Nn состоит из 10 - 20 блоков нагружений. Следовательно, объем блока определится делением на это число прогнозируемой долговечности Nn. Универсальным (хотя и несколько специфическим) средством разделения процесса нагружения на блоки являются перегрузки, сопровождающие нормальный процесс эксплуатации горно-металлургического оборудования. Их число зависит от их относительного уровня к штатным нагрузкам. Разработаны методики формализации таких историй нагружения [17, 18].
Впрочем, и при мониторинге процесса нагружения Q(t), как правило, следует оперировать блоком нагружения, чтобы установить фактические значения a0 и аr. Обычно надежные характеристики сопротивления усталости (ХСУ) получают для стационарного нагружения, поэтому и возникает процедура суммирования повреждений, чтобы учесть фактор нестационарности. Если иметь базовые ХСУ, полученные при случайном нагружении, то в (1) будут иначе определяться элементарные повреждения dj , а повреждения a0 и аr можно принимать за единицу. Однако, такие ХСУ получают на дорогостоящих сервогидравлических испытательных машинах, а разрабатываемые на их основе модели сопротивления усталости могут быть или громоздкими, или нечувствительными к отклонениям реального процесса нагружения от испытательного, при котором получены модели.
Предлагаемая ресурсная модель сопротивления усталости пригодна для обоих диагностических признаков.
Чтобы использовать детерминированную модель нагружения при мониторинге ТС, необходимо, как уже установлено, найти допускаемое повреждение [D] по гарантированной долговечности NR, рассчитанной с учетом внешнего и внутреннего факторов (рис. 5.3). Характеристики рассеяния долговечности при стационарном и нестационарном нагружении, обусловленные только внутренним фактором одинаковы и зависят от медианной величины 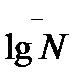 . Известно также, что коэффициент вариации накопленного повреждения совпадает с коэффициентом вариации долговечности: vD=vN. Используя взаимосвязь между нормальным и логнормальным распределениями, получаем равенство СКО логарифмов повреждения и долговечностей:
. Известно также, что коэффициент вариации накопленного повреждения совпадает с коэффициентом вариации долговечности: vD=vN. Используя взаимосвязь между нормальным и логнормальным распределениями, получаем равенство СКО логарифмов повреждения и долговечностей:
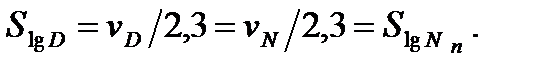 (5.3)
(5.3)
При этом величина vN определяется через коэффициенты вариации внутреннего va и внешнего vy факторов:
vN  =
= 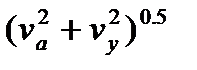 .
.
| lgD |
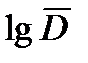 βR1 βR1
|
| lg[D] |
| lgNR |
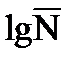
|
| lgN |
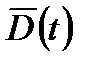
|
| f(lgN) |
| fR(lgN) |
Рис. 5.3. Нахождение допускаемого повреждения [D] по распределению долговечностей, заданному его плотностью f(lgN), для безопасности R
Внешняя составляющая разброса накопленного повреждения при диагностировании ТС определяется точностью регистрации процесса измерительными средствами, хотя при прогнозировании назначенного ресурса имеется особая методика расчета vy по принятому спектру [18]. Учитывая, что СКО величины 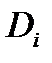 , составляет
, составляет 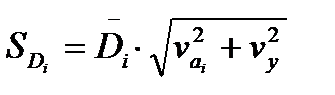 при мониторинге нагружения, когда величину vy не нужно прогнозировать, происходит отмеченное уточнение оценки ресурса.
при мониторинге нагружения, когда величину vy не нужно прогнозировать, происходит отмеченное уточнение оценки ресурса.
Внутренняя составляющая разброса накопленного повреждения постоянна и связана с одной из основных ХСУ SlgN, члены уравнения которого A, kSN, NA определяются непосредственно при усталостных испытаниях или выбираются по рекомендациям из справочников для соответствующего материала и элемента конструкции:
 (5.4)
(5.4)
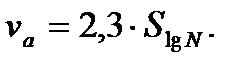 (5.5)
(5.5)
Представив процесс накопления повреждений в двойных логарифмических координатах (рис. 5.3), получаем распределение величины lgD аналогичным распределению lgN:
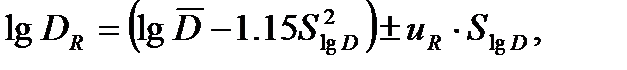 (5.6)
(5.6)
где uR – квантиль нормального распределения для вероятности R.
Установив требуемый уровень безопасности R, приравняв DR=1 (тогда lgDR=0), получаем:

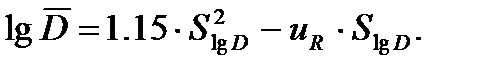 (5.7)
(5.7)
Если задавать допустимый уровень риска, то перед вторым сомножителем следует ставить знак «+». В принятой позиции величина 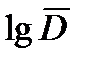 принимает смысл допустимого повреждения. При гарантированном уровне безопасности P=98%, принятом в общем машиностроении, полагая
принимает смысл допустимого повреждения. При гарантированном уровне безопасности P=98%, принятом в общем машиностроении, полагая 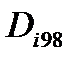 =1, допускаемая величина повреждения будет:
=1, допускаемая величина повреждения будет:
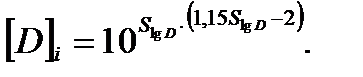 (5.8)
(5.8)
Остаточное число циклов нагружения до прекращения эксплуатации детали на момент контроля i будет:
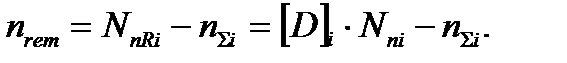 (5.9)
(5.9)
Вынося за скобки значение числа циклов наработки nΣi, которое контролируется, окончательно имеем:
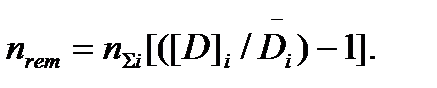
(5.10)
Здесь черта над символом текущих повреждений подчеркивает то, что оперировать следует серединными значениями.
Допускаемая величина 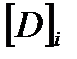 непостоянная и определяется усредненной скоростью исчерпания ресурса (
непостоянная и определяется усредненной скоростью исчерпания ресурса ( 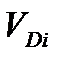 , рис. 5.2). Для установившегося процесса величина
, рис. 5.2). Для установившегося процесса величина 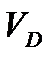 постоянна. Однако, значения
постоянна. Однако, значения 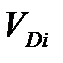 для разных моментов оценки ресурса после нараб отки nΣi
для разных моментов оценки ресурса после нараб отки nΣi  будут разными и необходимо производить пересчет
будут разными и необходимо производить пересчет 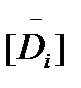 .
.
Точность данной оценки ресурса определяется величиной 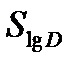 . Если для определения
. Если для определения 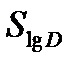 =
= 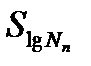 применять общепринятые методики, базирующиеся на представлении нагружения в виде итогового спектра и корректировке повреждения, инвариантной к асимметрии цикла и характеру чередования нагрузок (истории нагружения), то прогнозируемый разброс долговечности
применять общепринятые методики, базирующиеся на представлении нагружения в виде итогового спектра и корректировке повреждения, инвариантной к асимметрии цикла и характеру чередования нагрузок (истории нагружения), то прогнозируемый разброс долговечности 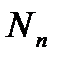 будет широк, что даст низкую оценку допускаемого повреждения. Для приведенного ниже в примере режима нагружения при безопасности P=98% допускаемое повреждение, рассчитанное таким методом, составляет
будет широк, что даст низкую оценку допускаемого повреждения. Для приведенного ниже в примере режима нагружения при безопасности P=98% допускаемое повреждение, рассчитанное таким методом, составляет 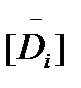 = 0,25.
= 0,25.
При применении для оценки ресурса на стадии эксплуатации методик, базирующихся на расширенных ХСУ, отражающих историю нагружения, величина 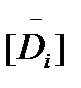 =0,35…0,43, в зависимости от повреждаемости процесса.
=0,35…0,43, в зависимости от повреждаемости процесса.
Представив кинетику повреждений линейной моделью, из подобия треугольников OAB и OCE (рис.5.4) имеем пропорцию 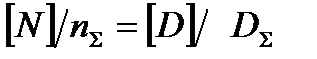 . Тогда в данных символах индекс безопасности определится через повреждения как:
. Тогда в данных символах индекс безопасности определится через повреждения как:
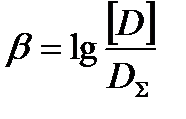 .
.
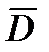
|
| [D] |
| [N] |
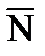
|
| C |
| B |
| A |
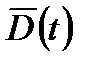
|
| DΣ |
| E |
| nΣ |
| Число циклов, время |

Рис. 5.4. К определению индекса безопасности по накоплению
повреждений
Поскольку допускаемое повреждение имеет вероятностный смысл, так как оно подсчитано для безопасности R, то и ее индекс, найденный по данной формуле, также может трактоваться как βR. Также вероятностную трактовку имеет и степень выработки (исчерпания) ресурса: 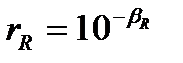 .
.
В разработанном диагностическом алгоритме предельная величина повреждения принята за единицу (как и весь безопасный ресурс). Тогда степень выработки ресурса принимает смысл и величину текущего повреждения Di в вероятностном аспекте:
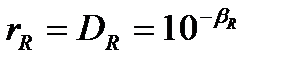 . (5.11)
. (5.11)
Изменение значений βR и rR происходит непрерывно за счет накопления повреждений Di (произвольная модель нагружения), DΣ (блочная модель нагружения) при эксплуатации, а также скачкообразно при пошаговой переоценке гарантированного ресурса и допускаемого повреждения [D]. Однако, подобные скачки на графике функции безопасности βR(t) отражаются, если вычислять индекс безопасности по теоретической зависимости, получаемой из его определения как логарифма гарантированного запаса долговечности (рис. 5.5).
При мониторинге процесса наработки индекс безопасности вычисляется через повреждения и график βR(t) имеет, как показывает практика, монотонно убывающий вид (рис. 5.5).
| βR |
| βR0 |
| βR1 |
| βR2 |
| βRi |
| nΣ1 |
| nΣ2 |
| nΣi |
| NnR0 |
| NnR1 |
| NnR2 |
| log (числа циклов) |
Рис. 5.5. Формирование графика изменения индекса безопасности при переоценке гарантированной долговечности NnR1, 2…i (тонкие линии), а также при мониторинге наработки nΣ1, 2…i (жирные линии) по накоплению усталостных повреждений
Дата добавления: 2015-03-14; просмотров: 699;
