Элементов конструкций
Рассмотрим для примера режим нагружения, формализованный двухступенчатыми блоками с относительными длительностями базовой ступени сB=0,99 и перегрузочной сOL=0,01. Распределение уровней цикловой повреждаемости ступеней, характеризующие их нагруженность, подчиняется нормальному закону (рис. 5.6, а):
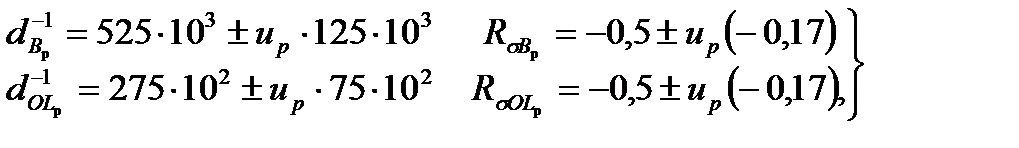 (5.12)
(5.12)
где dB и dOL - элементарные (за один цикл нагружения) повреждения,
соответственно, на базовой и перегрузочной ступени,
RσB и RσOL - коэффициент асимметрии цикла, соответственно, на базовой и
перегрузочной ступени,
uр - квантиль нормального распределения для вероятности P.
| σ/МПа |
| 0,10 |
|
| P |
| d-1 |
| 105 |
| 104 |
| 106 |
| 0,01 |
| 0,90 |
| 0,99 |
| б |
| а |
| 0,50 |
|
Рис. 5.6. Распределение нагрузок в повреждениях (а) и напряжениях (б) на нормальной вероятностной сетке (1) и его ступенчатая аппроксимация (2)
Такая модель нагружения отражает последовательность чередования ступеней (в частности, появление перегрузок), при которой можно учесть изменение (корректировку) величины а0. В данном примере межблочное повреждение а0 определялось по полиномиальной модели. На рис. 5.6, б изображено более привычное частотное распределение этого процесса в эквивалентных симметричному циклу напряжениях. Для перехода от элементарных повреждений dj к напряжениям использовалась модель сопротивления усталости, приведенная в работе [19].
Совокупность воздействий двухступенчатыми блоками (5.12) за длительный период дает такой итоговый спектр. Ему соответствует стандартный блок объемом 20000 циклов на основе биномиального распределения с параметром р=0,5 [20], для которого приведены амплитудные напряжения σa для симметричного цикла, и максимальные напряжения σmax для отнулевого цикла. Эквивалентирование этого блока (2, рис. 5.6, б, табл. 5.1) осуществлено по повреждающему действию, оцениваемому как Σdj∙cj.. Для обоих блоков (двухступенчатого и шестиступенчатого) этот параметр равен 2,25∙10-6.
Таблица 5.1
Параметры эквивалентного блока нагружения
| j ступени | ||||||
| nj, циклов | ||||||
| cj | 0,0003 | 0,0027 | 0,02 | 0,09 | 0,28 | 0,607 |
| dj-1 | ||||||
| σa, МПа (Rσ=-1) | ||||||
| σmax, МПа (Rσ=0) |
Таблица 5.2
Показатели циклического нагружения блок-случайного процесса
(рандомизированная последовательность блоков)
| № блока | σВ, МПа | σOL, МПа | RB | ROL | 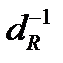
| 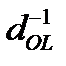
|
| -0,44 | -0,42 | |||||
| -0,74 | -0,22 | |||||
| -0,48 | -0,58 | |||||
| -0,39 | -0,17 | |||||
| -0,22 | -1,0 | |||||
| -0,29 | -0,61 | |||||
| -0,50 | -0,29 | |||||
| -0,60 | -0,63 | |||||
| -0,39 | -0,33 | |||||
| -0,52 | -0,48 | |||||
| -0,44 | -0,42 | |||||
| -0,74 | -0,22 | |||||
| -0,48 | -0,58 | |||||
| -0,39 | -0,17 |
Очевидно, должны бы быть одинаковыми результаты расчета гарантированного ресурса, допускаемого повреждения и функции безопасности для обоих моделей нагружения. Для проверки этого суждения были проведены усталостные испытания металлических образцов, для которых и была получена использованная модель ХСУ [19]. Режим блок-случайного нагружения образцов, получаемый методом Монте-Карло по модели (5.12), приведен в таблице 5.2. Предварительно для шестиступенчатого блока по методике Серенсена-Когаева была получена функция распределения долговечности, по которой найдена соответствующая функция индекса безопасности для R=0,98 ( 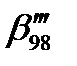 , рис. 5.7).
, рис. 5.7).
В данном случае для нахождения уравнения индекса безопасности используется его формулировка как βR=lgNnR -lgnΣ. При моделировании нагружения в виде спектра для приведенных условий получаем: lgNn98=4,14.
Исходя из модельных представлений, разница между диагностированием с использованием контроля наработки nΣ(t) и с использованием конроля нагружения Q(t) заключается в наличии существенного коэффициента вариации внешнего фактора vy для первого случая, и в его, практическом, отсутствии во втором. Чтобы экспериментально подтвердить этот факт, нужно в первом случае при испытаниях для каждого образца реализовывать разные истории нагружения, состоящие из двухступенчатых блоков с разными параметрами (имитация мониторинга наработки); в другом случае следует для каждого образца реализовывать одну и ту же историю нагружения, но разной продолжительности, фактически, осуществляя программное нагружение макроблоком, состоящим из двухступенчатых микроблоков (имитация мониторинга нагружения). Именно такой макроблок из 10 микроблоков каждый объемом 10000 циклов представлен в таблице 5.2. По результатам испытаний были получены функции распределения долговечностей и определено ее гарантированное значение, определяющее положение функции безопасности: lgNn98=4,85 (блок- случайное нагружение), lgNn98=5,00 (блок- программное нагружение). Таким образом, учет фактора истории нагружения позволил примерно в 5 раз продлить безопасный ресурс ( 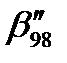 , рис. 5.7).
, рис. 5.7).
Идентификация деградационного усталостного процесса при диагностировании ТС механических систем технологического оборудования происходит по следующему алгоритму. При мониторинге процесса нагружения распознаются и измеряются циклы нагрузки, соответствующие ступеням формализованного блока. По ним определяются максимальные (амплитудные) напряжения (σВ и σOL, табл. 5.2) и асимметрии цикла, которым соответствуют элементарные повреждения в виде относительных долговечностей при стационарном нагружении. Кроме этого, регистрируется число циклов наработки. Если в формализованном блоке зафиксировано число циклов ступеней cj (в примере cOL/cB=1/100), то достаточно контролировать общее число циклов наработки nΣ.
Для каждого блока по полиномиальной модели [19] определяются скорректированные значения внутриблочного повреждения a0 (табл. 5.3), а также по (1) рассчитываются медианные значения итоговой долговечности, приняв ar=0,7 (табл. 5.4). СКО логарифмов долговечностей SlgN определялось по зависимости (2), где A=0,175, kSN,=0,075, NA=105.
Таблица 5.3
Накопление повреждений при блок-случайном процессе
| № блока | a0 | Dλ | DΣ | [D] | β98 |
| 1,06 | 0,034 | 0,034 | 0,440 | 1,11 | |
| 0,80 | 0,036 | 0,07 | 0,448 | 0,81 | |
| 0,79 | 0,046 | 0,116 | 0,460 | 0,60 | |
| 1,12 | 0,02 | 0,136 | 0,420 | 0,49 | |
| 0,65 | 0,033 | 0,169 | 0,443 | 0,42 | |
| 0,87 | 0,026 | 0,195 | 0,430 | 0,34 | |
| 0,79 | 0,027 | 0,222 | 0,433 | 0,29 | |
| 0,66 | 0,033 | 0,255 | 0,442 | 0,24 | |
| 0,76 | 0,018 | 0,273 | 0,413 | 0,18 | |
| 0,66 | 0,03 | 0,303 | 0,437 | 0,16 | |
| 1,06 | 0,034 | 0,357 | 0,440 | 0,12 | |
| 0,80 | 0,036 | 0,373 | 0,448 | 0,08 | |
| 0,79 | 0,046 | 0,419 | 0,460 | 0,04 | |
| 1,12 | 0,02 | 0,439 | 0,420 | -0,02 |
Повреждение, вносимое каждым блоком нагружения, вычислялось как:
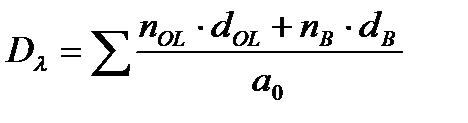 . (5.13)
. (5.13)
Общее накопленное повреждение определяется как DΣ=(ΣDλ)/ar. Остальные параметры деградационного процесса (табл. 5.3, 5.4) находились по (5.1) - (5.10).
В процессе нагружения образцов контроль показателей ТС производился через каждый блок, то есть 14 раз. Диагностирование показывает, что ресурс материала вырабатывается к середине 14 блока (r98>1). На самом деле к этому сроку образцы еще не разрушались. Они входили в зону риска (рис. 5.7), где показатели ТС оцениваются по иным моделям. Реальная кинетика изменения индекса безопасности ( 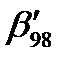 , рис.5.7), в целом, отвечает теоретическому ходу функции βR(t) (графики
, рис.5.7), в целом, отвечает теоретическому ходу функции βR(t) (графики 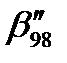 ,
, 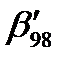 практически, параллельны). Это свидетельствует о равномерном уменьшении индекса безопасности за каждый блок, что подтверждает состоятельность этого показателя для оценки ТС. Сравнивая долговечности, при которых β98=0,можно констатировать, что идентификация деградационной модели дает возможность продлить срок эксплуатации в 2 раза по сравнению с диагностированием посредством контроля наработки, и в 10 раз по сравнению с исходным ресурсом.
практически, параллельны). Это свидетельствует о равномерном уменьшении индекса безопасности за каждый блок, что подтверждает состоятельность этого показателя для оценки ТС. Сравнивая долговечности, при которых β98=0,можно констатировать, что идентификация деградационной модели дает возможность продлить срок эксплуатации в 2 раза по сравнению с диагностированием посредством контроля наработки, и в 10 раз по сравнению с исходным ресурсом.
Таблица 5.4
Ресурсные показатели при блок-случайном процессе нагружения
| № блока | SlgN | 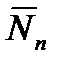
| nrem98 | r98 |
| 0,199 | 0,077 | |||
| 0,197 | 0,156 | |||
| 0,189 | 0,252 | |||
| 0,215 | 0,32 | |||
| 0,200 | 0,38 | |||
| 0,208 | 0,45 | |||
| 0,206 | 0,51 | |||
| 0,200 | 0,58 | |||
| 0,220 | 0,66 | |||
| 0,203 | 0,69 | |||
| 0,199 | 0,76 | |||
| 0,197 | 0,83 | |||
| 0,189 | 0,91 | |||
| 0,215 | 1,04 |

Рис. 5.7. Изменение индекса безопасности β98 в процессе наработки nΣ, полученное при моделировании нагружения итоговым спектром (β```98); при контроле наработки (β``98); при мониторинге нагружения (β`98), а также при этом кинетика исчерпания ресурса (r98).
Выводы
1. Для прогнозирования технического состояния (ТС) следует выбирать такие диагностические параметры, у которых можно установить их предельные значения, обусловленные природой деградационного процесса (прогнозирование работоспособности) или связанные с качеством выполняемых объектом операций (прогнозирование исправности). Диагностические параметры, у которых можно установить лишь эталонные показатели, пригодны только для оценки ТС. Например, форма временного сигнала нагружения главной линии прокатного стана дает информацию об изношенности сочленений и о качестве подготовки обрабатываемого металла. Но для прогнозирования срока службы деталей, определяющих безопасность механической системы, данный признак пригоден лишь как основа для оценки накопленного повреждения, отражающего деградационный усталостный процесс, происходящий в металле конструкции.
2. В качестве косвенных диагностических параметров для прогнозирования ТС механических систем технологического оборудования предлагаются индекс безопасности и степень выработки (исчерпания) ресурса, которые оцениваются по прямым диагностическим признакам- временным реализациям процесса нагружения Q(t) или прцесса наработки nΣ(t). В первом случае возможно продлить безопасный ресурс в 10 раз, а во втором случае в 5 раз по сравнению с исходным ресурсом. Столь значительный эффект достигнут для элементов конструкций, рассчитанных на ограниченную долговечность. Для объектов, рассчитанных на длительный срок службы эффект от мониторинга ТС в относительном выражении будет меньше, хотя абсолютное время продления будет весьма немалым.
3. Мониторинг процесса нагружения более информативен по сравнению с отслеживанием числа циклов наработки, позволяя исключить фактор случайности в алгоритме оценки безопасности (межблочное повреждение аr) и за этот счет продлить срок безопасной эксплутации.
4. Переход от моделирования нагруженности механических систем технологического оборудования частотным распределением (итоговым спектром) к моделированию процесса нагружения формализованным блоком (типовой историей нагружения) со случайно изменяющимися параметрами позволяет использовать в качестве диагностического признака при прогнозировании работоспособности число циклов наработки. Это позволяет избежать оснащения оборудования сложными системами наблюдения за условиями эксплуатации, что актуально для действующих объектов.
Дата добавления: 2015-03-14; просмотров: 661;
