Формула ідеального радіопередавання
Знайдемо співвідношення, що формально дозволять розрахувати значення напруженості електричного поля Е в дальній зоні будь-якого випромінювача, розташованого в вільному просторі. Припустимо, що випромінювач є ізотропним. Енергія радіохвилі, що збуджується випромінювачем, розподіляється рівномірно по поверхні уявної сфери радіуса r. Енергія W, що випромінюється за одиницю часу, визначає потужність випромінювання 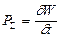 . Якщо потужність випромінювання
. Якщо потужність випромінювання 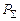 відома, то в будь-якій точці дальньої, тобто хвильової зони, можна знайти середнє значення вектора Пойнтінга Пср, який є потоком енергії, що переходить за одиницю часу крізь одиницю поверхні й має розмірність Вт/м2:
відома, то в будь-якій точці дальньої, тобто хвильової зони, можна знайти середнє значення вектора Пойнтінга Пср, який є потоком енергії, що переходить за одиницю часу крізь одиницю поверхні й має розмірність Вт/м2:
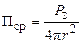 . (2.1)
. (2.1)
Значення вектора Пойнтінга в точці прийому радіохвилі можна також визначити на підставі відомого співвідношення
Пср = 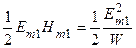 , (2.2)
, (2.2)
де 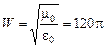 – хвильовий опір повітря,
– хвильовий опір повітря, 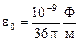 і
і 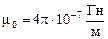 – його діелектрична й магнітна сталі, Em1 та Hm1 – амплітуди векторів напруженості електричного і магнітного полів, що створюються ізотропним випромінювачем у точці спостереження. Прирівнюючи праві частини співвідношень (2.1) і (2.2), встановлюємо залежність амплітудного значення напруженості
– його діелектрична й магнітна сталі, Em1 та Hm1 – амплітуди векторів напруженості електричного і магнітного полів, що створюються ізотропним випромінювачем у точці спостереження. Прирівнюючи праві частини співвідношень (2.1) і (2.2), встановлюємо залежність амплітудного значення напруженості 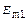 від потужності випромінювання
від потужності випромінювання 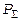 , справедливу для будь-якого всюдиспрямованого випромінювача:
, справедливу для будь-якого всюдиспрямованого випромінювача:
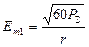 . (2.3)
. (2.3)
Нехай 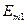 <
< 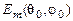 , де
, де 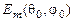 – максимальна напруженість поля, створюваного реальною антеною на відстані r від неї в напрямку, що визначається кутами q0 і j0. Таку ж напруженість поля на відстані r може забезпечити ізотропна антена, якщо її потужність випромінювання збільшити в D разів. При цьому співвідношення (2.3) можна відкоригувати, надавши йому такий вигляд:
– максимальна напруженість поля, створюваного реальною антеною на відстані r від неї в напрямку, що визначається кутами q0 і j0. Таку ж напруженість поля на відстані r може забезпечити ізотропна антена, якщо її потужність випромінювання збільшити в D разів. При цьому співвідношення (2.3) можна відкоригувати, надавши йому такий вигляд:
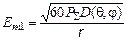 . (2.4)
. (2.4)
У співвідношенні (2.4) множник D – коефіцієнт спрямованої дії (КСД) антени. Він показує, в скільки разів треба збільшити потужність випромінювання ізотропної антени, щоб вона у необхідному напрямку (q, j) на віддалі r створювала таку ж напруженість поля, як і спрямована антена. Співвідношення (2.4) називається формулою ідеального радіопередавання.
Для врахування реальних умов поширення радіохвиль формулу ідеального радіопередавання помножують на множники, що враховують особливості місцевості, наявність рослин, закритість радіотраси по відношенню до горизонту та ін. При цьому в просторі можна виділити певні зони, які суттєво впливають на поширення радіохвиль.
2.2.2. Область простору, яка є суттєвою при поширенні радіохвиль
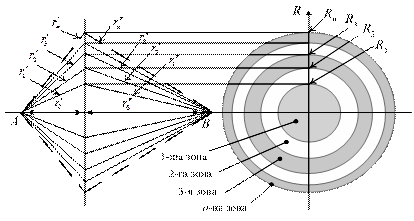
Припустимо, що радіохвиля збуджується ізотропним випромінювачем і поширюється з точки А до точки В (рис. 2.1). У відповідності із принципом Гюйгенса кожна точка фронту хвилі є елементарним збуджувачем сферичної хвилі, що поширюється "вперед". Таким чином, у точці спостереження В складаються хвилі, що збуджуються безліччю окремих елементів Гюйгенса, розташованих на поверхні фронту радіохвилі, що поширюється. Виявимо область простору, що є суттєвою для переносу тієї частини енергії радіохвилі, під дією якої збуджується приймальна антена, яка розташована у точці В.
Поміж точками А і В виділимо фрагмент уявної плоскої поверхні S, нехтуючи його кривизною. Слід фрагмента на рис. 2.1, а, зображений у вигляді прямої, що перпендикулярна лінії АВ. Кожна точка цього фрагмента збуджує в точці В, що знаходиться на відстані 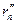 , де n = 1,2,3,..., електричне поле, що характеризується напруженістю En. Відстань
, де n = 1,2,3,..., електричне поле, що характеризується напруженістю En. Відстань 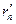 від точки А до відповідної точки, що лежить на поверхні S, разом з відстанями
від точки А до відповідної точки, що лежить на поверхні S, разом з відстанями 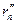 утворять шлях, який проходить елементарна n-а хвиля між точками А та В. Відстані
утворять шлях, який проходить елементарна n-а хвиля між точками А та В. Відстані 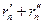 оберемо таким чином, щоб вони відрізнялися від відстані
оберемо таким чином, щоб вони відрізнялися від відстані 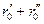 на величину
на величину 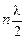 .
.
а) б)
Рис.2.1
Користуючись прийнятими позначеннями, запишемо вираз:
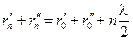 . (2.5)
. (2.5)
При цьому на уявній поверхні S можна виділити концентричні кола радіусів R1, R2, ... Rn (рис. 2.1, б). На цьому рисунку R – поточний радіус, а 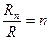 . Ділянки поверхні, які обмежені цими колами, називають зонами Френеля. Перша зона Френеля - це коло радіуса R1. Зони вищих порядків – кільцеві. Ширина кілець визначається різницями радіусів Rn - Rn-1, що обмежують n-ю зону Френеля. Фази хвиль, які створені в точці В вторинними випромінювачами (елементами Гюйгенса), розподіленими по площинам відповідних зон Френеля, уявно виділених на поверхні S, відрізняються на 1800. Тому в точці В відбувається часткова взаємна компенсація амплітуди результуючої радіохвилі.
. Ділянки поверхні, які обмежені цими колами, називають зонами Френеля. Перша зона Френеля - це коло радіуса R1. Зони вищих порядків – кільцеві. Ширина кілець визначається різницями радіусів Rn - Rn-1, що обмежують n-ю зону Френеля. Фази хвиль, які створені в точці В вторинними випромінювачами (елементами Гюйгенса), розподіленими по площинам відповідних зон Френеля, уявно виділених на поверхні S, відрізняються на 1800. Тому в точці В відбувається часткова взаємна компенсація амплітуди результуючої радіохвилі.
Визначимо радіуси Rn зон Френеля. З розгляду рис. 2.1 випливає така система рівнянь:
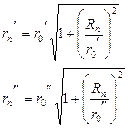 .
.
У відповідності до формули (2.3) напруженості електричних полів, збуджених елементами Гюйгенса, що розташовані у зонах Френеля вищих порядків, значно менші за напруженості полів, збуджених зонами нижчих порядків тому, що 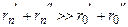 . У зв'язку з цим можна припустити справедливість таких нерівностей: Rn<<
. У зв'язку з цим можна припустити справедливість таких нерівностей: Rn<< 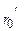 та Rn<<
та Rn<< 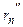 . Тому, розкладаючи праві частини співвідношень (2.5) у ряд і утримуючи в ньому перші два доданки, отримаємо приблизні рівності
. Тому, розкладаючи праві частини співвідношень (2.5) у ряд і утримуючи в ньому перші два доданки, отримаємо приблизні рівності
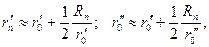
з яких випливає, що відстань між точками А й В (рис. 2.1,а) визначається співвідношенням:
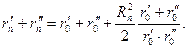 (2.6)
(2.6)
Зіставляючи формули (2.5) та (2.6), знаходимо радіус n-ої зони Френеля:
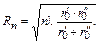 (2.7)
(2.7)
Площі всіх зон Френеля для наданого співвідношення між відстанями 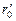 й
й 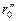 однакові. Вони надаються виразом:
однакові. Вони надаються виразом:
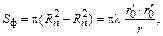
де 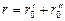 – найкоротша відстань між точками А й В.
– найкоротша відстань між точками А й В.
Дата добавления: 2015-03-14; просмотров: 1157;
