Елементарні електромагнітні вібратори

1.3.1. Елементарний електричний вібратор (диполь Герца)

Електричний вібратор – це пристрій, в якому можуть виникати високочастотні коливання струму. Такий пристрій можна використовувати для збудження електромагнітних полів у навколишньому просторі або для приймання радіосигналів з простору. Елементарним вібратором (диполем Герца) є короткий відносно довжини хвилі відрізок прямолінійного тонкого дроту з рівномірним розподілом струму 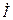по довжині та електричними зарядами на його кінцях. З рівнянь Максвела випливає, що такий провідник здатний збуджувати електромагнітне поле, яке поширюється у просторі.

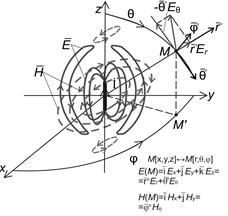
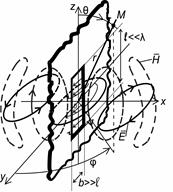
Розмістимо диполь Герца в початку прямокутної системи координат M[X,Y,Z] уздовж поздовжньої вісі Z (рис. 1.2). На підставі рівнянь Максвела, навколо струму зображено магнітні силові лінії , що розташовуються в горизонтальних площинах і мають такі проекції: 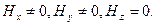Електричні заряди, що пов’язані зі струмом 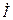законом збереження заряду, на підставі четвертого рівняння Максвела є джерелами електричного поля 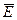, силові лінії якого починаються та закінчуються на полюсах диполя і мають розімкнений характер. При цьому вектор 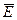має всі проекції, тобто 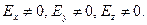У свою чергу, змінне електричне поле на підставі першого рівняння Максвела є джерелом вихрового змінного магнітного поля, яке далі породжує змінне електричне, й т. п.

Структура поля диполя Герца відображена на рис.1.2 сукупністю електричних та магнітних силових ліній. Вона не залежить від типу координатної системи, тому перейдемо до сферичної системи координат 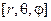, яка є більш зручною, оскільки фронт хвилі має форму сфери. При цьому аналізу підлягають складові :

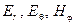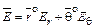; (1.1),

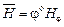, (1.2),

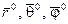– орти сферичної системи координат.

У точці спостереження 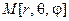означені вектори створюють локальну прямокутну систему координат. Осями цієї системи є подовження радіусу r, дотична до дуги вертикального кута 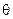, та дотична до дуги горизонтального кута 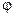. Значення складових векторів 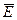(1.1) та 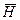(1.2) визначаються на основі рівнянь Максвела [2]:

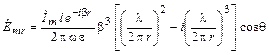; (1.3)

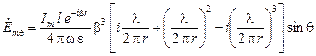; (1.4)

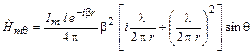, (1.5)

де 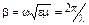- коефіцієнт фази або хвильове число.

Слід зазначити, що кожна складова електромагнітного поля містить компоненти (додатки), що по-різному залежать від відстані r. Тому при 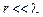та 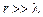в (1.3) – (1.5) домінують окремі складові й поля відрізняються за характером поширення та властивостями. Відповідно до цього, у просторі навколо випромінювача умовно розрізняють три зони:

- ближня зона (при 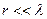), яку ще називають зоною коливань або зоною індукції;

- проміжна зона (при 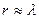), яку називають зоною Френеля);

- дальню зону (при 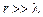), яку називають хвильовою зоною або зоною Фраунгофера.

В каналах радіозв’язку, як правило, виконуються умови дальньої зони. Тому співвідношення (1.3) – (1.5) для цих умов можна спростити:

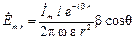; (1.6)

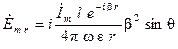; (1.7)

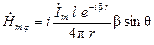; (1.8)

Із співвідношень (1.6) та (1.7) випливає, що в дальній зоні кривизна фронту хвилі зменшується і форма його певної ділянки, що досліджується, стає майже плоскою. Домінуючі поперечні складові поля (1.7) та (1.8) є синфазними та пов’язані коефіцієнтом пропорційності – хвилевим опором (табл.1.1):

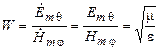(1.9)

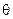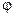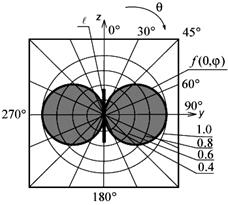
Амплітудна характеристика (діаграма) спрямованості диполя Герца визначається співвідношенням (1.7) або (1.8) як залежність напруженості поля від кутових координат та при 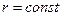. З розгляду рис. 1.2 та співвідношення (1.7) випливає, що нормована ДН диполя Герца 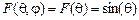має форму тороїда (рис.1.3), тобто в горизонтальній площині ДН має форму кола, а у вертикальній – «вісімки». Це означає, що диполь Герца в дальній зоні має максимум випромінювання у напрямку, перпендикулярному до його осі, а в напрямку осі не випромінює. Такими саме властивостями характеризується диполь Герца в режимі приймання радіохвиль з простору. Ширина головної пелюстки ДН у вертикальній площині має значення .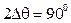

Основні характеристики диполя Герца відповідно до табл.1.1:

- потужність випромінювання

-

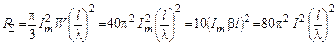, (1.10)

де 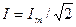- ефективне (діюче) значення сили струму,

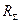- опір випромінювання

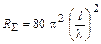; (1.11)

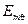- амплітуда напруженості електричної складової поля

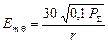; (1.12)

D = 1,5 - коефіцієнт спрямованої дії;

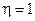- коефіцієнт корисної дії;

G = D = 1,5 - коефіцієнт підсилення.

Однією з основних властивостей диполю Герца є те, що він не випромінює вдовж власної осі, а максимум випромінювання спостерігається перпендикулярно до його осі.

1.3.2. Елементарний рамковий вібратор

Якщо елементарний електричний вібратор, подібний до розглянутого вище, зігнути в кільце навколо осі Z, то отримаємо елементарний рамковий (кільцевий) вібратор із структурою поля, що збуджується струмом 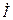(рис. 1.4, а). З цього рисунку випливає, що при означеному просторовому положенні рамкового вібратора його поле є симетричним відносно осі Z.

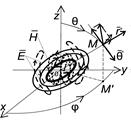
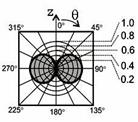
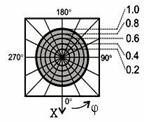
Оскільки в точках з координатами 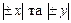напруженості електричного поля однакові за модулем й протилежні за напрямками (знаками), то в будь-якій точці на осі Z при 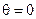результуюча напруженість E = 0, а при 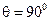результуюча напруженість сягає максимального значення. Тому в будь-якому вертикальному перерізі діаграма спрямованості має форму горизонтальної «вісімки» (рис.1.4, б), тобто 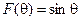, а в горизонтальному – форму кола (рис.1.4, в), тобто .

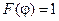Таким чином, в просторі ДН рамкового вібратора має вигляд, подібний до зображеного на рис.1.3, при якому рамка не випромінює

вдовж осі Z. Тому рамковий вібратор може бути представлений як умовний елементарний електричний вібратором, що збуджується гіпотетичним магнітним струмом 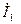. При цьому, відносно диполя Герца з електричним струмом, в структурі поля (рис.1.4, а) силові лінії 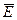замінюються лініями 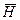та навпаки, на підставі властивості переставної двоїстості рівнянь Максвела. Такий диполь із струмом 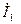, еквівалентний за своєю дією елементарному витку з електричним струмом, називають магнітним диполем. Основні співвідношення для компонент поля, що характеризують рамковий вібратор, є такими:

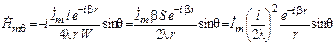(1.13)

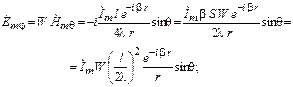(1.14)

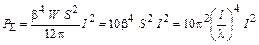; (1.15)

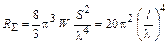, (1.16)

де 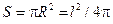- площа витка радіусу R та довжиною l.

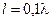З порівняння співвідношень (1.11) та (1.15) випливає, що при інших рівних умовах, потужність випромінювання диполя Герца перевищує потужність випромінювання елементарного рамкового вібратора в рази. Наприклад, при або 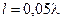відповідні перевищення потужності випромінювання сягають 400 та 40000 разів. Тому одновиткові рамкові антени доцільно використовувати лише як приймальні.

1.3.3. Елементарний щілинний вібратор

Якщо в безмежному металевому листі прорізати щілину з розмірами, значно меншими за довжину хвилі (рис.1.5), та до її країв прикласти змінну напругу U, то в розкриві щілини виникне змінне електричне поле напруженістю 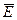. Далі, на підставі першого та другого рівнянь Максвела, в просторі створюється власно електромагнітна хвиля. Таким чином, можна отримати елементарний щілинний вібратор, еквівалентом якого за

структурою поля можна вважати магнітний диполь, орієнтований вдовж осі Z. З розгляду рис. 1.5 випливає, що в дальній зоні домінують складові 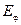та 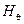, а нормована діаграма спрямованості має форму тороїда, оскільки ХН щілини 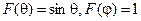подібна до зображеної на рис.1.2 та 1.3. Щілина випромінюватиме, якщо вона перетинає лінії струмів провідності в металевому листі, наприклад, у стінці хвилеводу.

1.3.4. Елемент Гюйгенса

Елементарні вібратори, які вже розглянуті, характеризуються симетричними двопелюстковими ДС типу 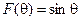. Але в багатьох практично важливих випадках необхідно мати системи з односпрямованим випромінюванням (прийомом) радіохвиль. Вібраторну систему з однопелюстковою ДС можна отримати при суміщенні двох взаємоперпендикулярних вібраторів - диполя Герца та рамкового вібратора, що розташовані в поперечній площині XOY (рис.1.6, а, б) Тут двопелюсткові діаграми відносяться до вібраторів, що розташовані в площинах рисунків, а ДС у вигляді кола – до вібраторів, що перпендикулярні площинам рисунків.

Припускається, що відповідні струми в обох незалежних вібраторах є такими, що напруженості полів у будь-якій точці дальньої зони є однаковими. При цьому сумарні нормовані ДС системи вібраторів мають форму кардіоїди 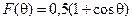, тобто така система є спрямованою з максимумом випромінювання в напрямі кута .

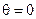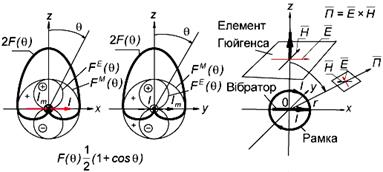
Система є технічно реалізуємою, якщо в ній магнітний вібратор з гіпотетичним магнітним струмом 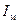замінити на еквівалентний йому за своєю дією виток із реальним електричним струмом I. Така система зображена на рис.1.6, в. З розгляду цього рисунку випливає, що така система має максимум випромінювання здовж осі Z (обидва струми є сонапрямленими). У дальній зоні вектор 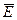є паралельним струму I та породжує в тій ж точці простору відповідну перпендикулярну складову вектора 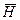, і таким чином 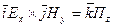. Нескінчене малий елемент уявної хвилевої поверхні, в якій знаходяться вектори 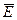та 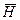, називається елементом Гюйгенса. Ці вектори є наслідками реальних елементарних струмів. Елемент Гюйгенса є моделлю вторинного джерела хвилі і породжує собі подібні. Він випромінює тільки «вперед» і дозволяє створити наочну модель процесу поширення фронту хвилі у вільному просторі.

Конструктивна сукупність реальних електричного вібратора та рамки із електричним струмом є найпростішим прототипом антени, ДС якої має чітко означений нуль, наприклад, у радіопеленгаторі – системи визначення координат об’єкту, що випромінює радіохвилі.

Ефективність елементарних вібраторів є незначною, оскільки амплітуда рівномірно розподіленого по довжині струму є дуже малою часткою гармонічного струму певного відрізка дроту, довжина якого сумірна до довжини хвилі 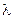. Очевидно, що геометричні розміри реальних вібраторів повинні бути кратними до величини 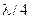, при яких реалізується принаймні один максимум та один мінімум амплітуди гармонічного струму. До таких антен відносяться дротові.