АНТЕННІ ПРИСТРОЇ

Электронная плотность.В соответствии с основными положениями квантовой механики распределение электронов в молекулах имеет вероятностный характер. Электронная плотность (плотность распределения вероятности для одного электрона) по определению равна:

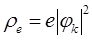
где 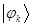- одноэлектронная волновая функция, описывающая состояние электрона в молекуле. В рамках 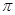- электронного приближения, последняя может быть записана

в виде разложения по 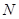атомным орбиталям 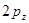- типа, т.е.

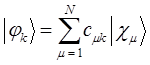
Молекулярные орбитали сопряжённых систем имеют делокализованный характер, поэтому электронная плотность в них будет распределена по всей молекуле.

При этом на каждом из атомов будет сосредоточена только определённая доля (часть) заряда электрона. Так, если на молекулярной орбитали 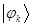с номером 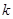находится один электрон, то доля его заряда, приходящаяся на атом с номером 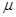, будет равна квадрату орбитального коэффициента 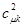. Величину 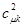называют 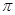- электронной парциальной плотностью на атоме 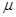. Если же на молекулярной орбитали 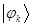с номером 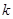находятся 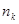электронов (в силу принципа Паули, очевидно, 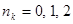), то их вклад в электронную плотность на атоме с номером 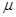, очевидно, будет равен 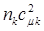. Если по всем молекулярным орбиталям ( 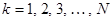) сопряжённой системы распределены 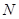электронов, то их суммарный вклад в 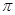- электронную плотность на атоме 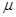равен соответственно:

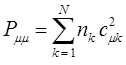
где 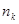- число заполнения молекулярных орбиталей электронами, т.е. число электронов на молекулярной орбитали 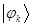с номером 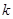. Величину 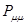называют также коулсоновской плотностью на атоме 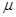. В методе молекулярных орбиталей Хюккеля предполагают, что в молекуле сопряжённого углеводорода имеется 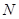атомов, каждый из которых даёт в 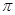- электронную систему по одному электрону. Следовательно, общее число 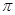- электронов в системе равно 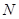. Поскольку электронная плотность на атоме – это доля заряда 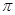- электронов, которые находятся у данного атома, то сумма электронных плотностей на всех атомах очевидно должна быть равна общему числу 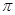- электронов системы. Учитывая условие нормировки волновой функции :

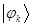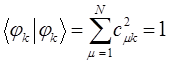
будем иметь соответственно:

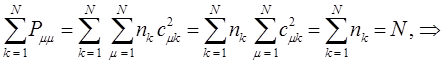
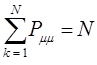
Значения электронной плотности принято указывать цифрами возле вершин молекулярного графа. Такое представление результатов расчёта называют молекулярной диаграммой.

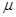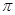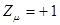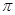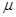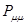Заряд на атоме. Если атом углерода с номером отдаёт в - электронную систему один электрон, он приобретает положительный заряд . Однако в результате делокализации некоторая часть - электронов сосредотачивается у атома. В силу этого электронная плотность на атоме равна . Тогда разность величин 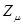и 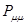будет определять остаточный заряд атома:

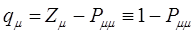
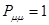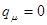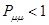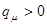при , ; при , ; при , .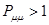

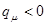Порядок связи. В классической химии оперируют целочисленными значениями порядка (кратности) связи. В приближении ЛКАО – МО, 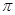- электроны делокализованны по всей молекуле, поэтому вклад в образование 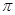- связи между любой парой атомов вносят электроны всех заполненных молекулярных орбиталей. В результате порядок связи в общем случае не будет являться целочисленной величиной. В методе же Хюккеля порядок (кратность) связи вычисляют по формуле:

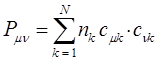
По аналогии с трактовкой 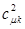произведение орбитальных коэффициентов 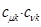можно интерпретировать как плотность электронов, сосредоточенную между двумя атомам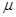и и 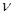. В общем случае, в приближении Хюккеля, порядок связи характеризует степень 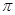- электронного связывания. Порядок локализованной 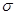- связи принимают равным единице 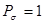. Тогда полный порядок кратной 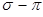- связи равен 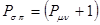. Очевидно, выражение для электронной плотности:

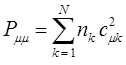
можно получить, если в уравнении:

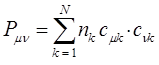
положить 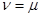. Все возможные для данной системы величины 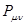можно собрать в матрицу размерности 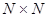. Такую матрицу 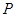называют матрицей порядков связей (или матрицей плотности первого порядка).

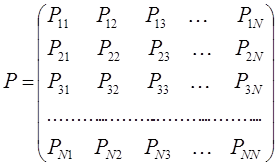
здесь диагональные элементы представляют собой электронные плотности на атомах 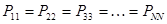, а недиагональные – порядки связей. Матрица порядков связей симметрична 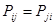. В хюккелевских расчётах молекул сопряжённых систем порядок связи между парами химически связанных атомов является относительно большой и положительной величиной. Следовательно, делокализация 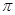- электронов двойных связей происходит по всей молекуле. Это в свою очередь означает, что в молекулах, где имеет место сопряжение, двойная связь существует в определённой мере между всеми атомами углерода. Результаты расчёта электронных плотностей и порядков связей, наносят на молекулярную диаграмму. Порядок связи тесно связан с такими характеристиками связей в молекуле, как силовая постоянная, рефракция и межатомное расстояние. Поскольку порядок связи 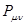представляет собой величину, характеризующую насыщенность углерод – углеродной связи 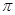- электронами, то очевидно, что больший порядок связи будет приводить к сокращению длины связи, поскольку в этом случае ядра должны как бы стягиваться к центру связи. Это в свою очередь позволяет предполагать обратно пропорциональную зависимость порядка связи от её длины:

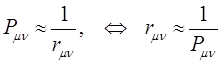
Впервые такая корреляция была исследована Коулсоном. Непосредственные хюккелевские расчёты ряда сопряжённых молекул подтверждают линейную зависимость длины связи от величины, обратной порядку 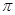- связи. Установим теперь взаимосвязь между порядком связи и полной 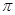- электронной энергией системы. Так, в методе МОХ 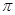- электронная энергия молекулы равна сумме орбитальных энергий, умноженных на соответствующие числа заполнения 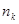электронами молекулярных орбиталей :

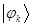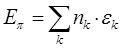
Поскольку по определению:

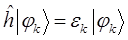
тогда соответственно:

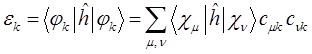
Как известно, в методе МОХ интегралы типа 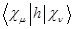заменяют параметрам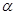и и 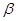, соответственно кулоновский и резонансный интегралы:

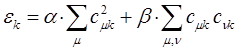
подстановка последнего выражения в соотношение:

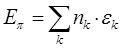
приводит к уравнению вида:

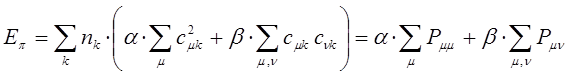
Индекс свободной валентности. В методе молекулярных орбиталей полный порядок связи 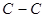может иметь, в общем, различные значения. Соответственно этому и реакционная способность атомов углерода может быть разной. Мерой реакционной способности в классической химии выступает свободная валентность (остаточное или парциальное сродство). В квантовой химии ей соответствует индекс свободной валентности, который определяют как разность между максимально возможным полным порядком связей и реальным полным порядком связей данного атома. Индекс свободной валентности на атоме 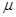вычисляют по формуле:

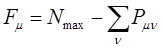
где 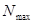- максимально возможная сумма порядков связей атома углерода в сопряжённой системе, а 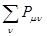- сумма порядков связей данного атома 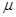со всеми соседними атомами. Расчёт показывает, что:

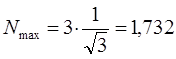
В связи с этим при вычислениях удобно использовать формулу вида:

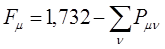
Индекс свободной валентности 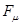характеризует степень участия данного атома в 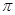- электронной системе. Его используют для предсказания способности сопряжённой системы принимать участие в радикальных реакциях. Индекс свободной валентности 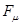обычно изображают на молекулярной диаграмме рядом со стрелкой, которую выводят из соответствующей вершины молекулярного графа.

Спиновая плотность. Данная величина является важнейшей характеристикой радикалов, характеризующая пространственное распределение неспаренного электрона. В случае, когда молекулярная орбиталь 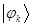заселена одним электроном, спиновая плотность 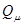на атоме 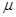равна квадрату орбитального коэффициента при атомной орбитали с номером 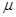. Величины 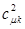определяют вероятность нахождения неспаренного электрона у данного атома. В общем случае, когда имеется несколько наполовину занятых молекулярных орбиталей, спиновые плотности вычисляются по формуле:

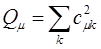
где суммирование проводится по орбиталям, заселённым одним электроном. Из приведенного выше выражения следует, что спиновая плотность на атомах, вычисленная в методе МОХ, всегда положительная величина. Однако из экспериментальных данных и из расчёта в рамках более строгих моделей известно, что спиновая плотность может быть отрицательной величиной. Физически это означает, что в соответствующих положениях преобладают электроны с проекцией спина 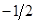( 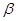-электроны). Теория Хюккеля сыграла выдающуюся роль в формировании теоретических основ органической химии. Множество концептуально важных понятий современной химии восходят к простому методу Хюккеля. Однако простота хюккелевской вычислительной схемы – оборотная сторона её недостатков. Среди основных недостатков метода – неучёт межчастичных взаимодействий (корелляционных эффектов). Это приводит к тому, что например изомеры, описываемые одной топологической матрицей и, как следствие, имеющие один и тот же набор молекулярных орбиталей, при расчётах оказываются неразличимыми. Так, ранее нами уже были рассмотрены приближения, присущие методу молекулярных орбиталей. Метод Хюккеля, помимо этих, содержит ряд дальнейших приближений, приемлемость которых в рамках более строгих теорий становится весьма сомнительной. Возникает вполне резонный вопрос, до какой степени можно оправдать эти приближения? Прежде всего, метод Хюккеля практически полезен потому, что не ставит перед собой слишком далеко идущих целей. В силу этого обстоятельства, в рамках метода Хюккеля практически невозможно получить количественное согласие экспериментальных и расчётных характеристик молекул. Действительно, метод Хюккеля не применяется для последовательного теоретического вычисления, каких – либо отдельных величин; он лишь позволяет установить связь одних экспериментальных данных с другими. Вычисляемые энергии, электронные плотности и другие величины выражены через параметры 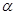и 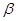. Формально эти параметры определены как интегралы, содержащие одноэлектронный гамильтониан 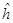, однако связь этого гамильтониана с полным гамильтонианом не конкретизируется. Перенос значени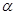й и 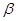, полученных для одного класса соединений в другой (например, из полиенов в ароматические соединения), недопустим и приводит к ошибкам. Внутри же одного класса соединений такой перенос возможен и даёт при расчёте приемлемые результаты. Так, в пределах одного класса соединений, имеет место хорошая корреляция экспериментальных и теоретически рассчитанных характеристик молекул. Однако значения 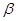, получающиеся во всех случаях, довольно сильно различаются между собой. Причина такого расхождения заключается в следующем: для вычисления энергии нужно использовать полный гамильтониан молекул, а не одноэлектронный гамильтониан метода Хюккеля. Если это учесть, то оказывается, что такие величины как энергии возбуждения, сродства к электрону и энергии диссоциации, выражаются не только через одни электронные интегралы типа 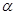и 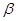, но зависят также от интегралов, описывающих межэлектронное взаимодействие. Принимая 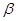как электрический параметр, можно в некоторых случаях (но не всегда) компенсировать пренебрежение этими интегралами. Но теперь при описании различных свойств молекул 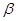представляет собою различные комбинации интегралов, и потому значения 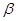, приводящие к согласию вычислений с экспериментальными данными в одном случае, могут отличаться от значений, являющихся наиболее подходящими для результатов экспериментов в другом случае. Именно поэтому не существует единых для всех молекул с гетероатомами значений параметров 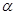и . 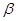Значение 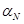, при котором лучше всего описывается основность содержащих азот гетероциклов, не обязательно является наилучшим для предсказания плотности неспаренного электрона в азотсодержащих радикалах, потому что 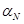при вычислении этих двух характеристик молекул выражает различные комбинации одно - и двухэлектронных интегралов. Изначально метод Хюккеля был разработан для изучения строения и свойств плоских сопряжённых углеводородов, и попытки его обобщения для расчёта более широкого набора молекулярных структур, к сожалению, оказались не столь удачными. Однако даже для случая сопряжённых систем известны молекулы, когда метод Хюккеля в его простейшей форме даёт довольно плохие результаты. Например, частота возбуждения молекулы бутадиена, вычисленная в рамках хюккелевского расчёта, составляет 35300 см^-1, а экспериментальное значение равно 46100 см^-1. Причина такого расхождения состоит в том, что не все длины связей в молекуле бутадиена одинаковы, а потому использование одного и того же значения 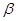для всех связей является грубым приближением. Хотя параметр 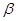не достаточно хорошо определён как величина, всё же ясно, что он должен быть приближённо связан с перекрыванием включённых в связь двух атомных орбиталей и с увеличением длины связи происходит его уменьшение по экспоненте. Для молекул, где имеет место сильное альтернирование связей, как, например, в сопряжённых полиенах, существенно, чтобы зависимость 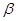от длины связи была учтена. Другой случай, когда нужно учитывать изменение 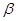, представляют молекулы, в которых участвующие в сопряжении атомы углерода не лежат в одной плоскости. Интересно отметить, что результаты, получаемые в рамках метода Хюккеля для альтернантных углеводородов, лучше, чем те, что получают для неальтернантных. Подведём некоторые итоги. Метод Хюккеля есть установления корелляционных связей между экспериментальными данными для классов родственных соединений. Это особенно полезно, когда рассматриваемый класс содержит большое число соединений (например, все ароматические углеводороды), а число используемых параметров мало. При переходе к системам, содержащим гетероатомы, как наблюдается, число параметров, которые следует определить на основе эксперимента, быстро растёт, и в то же время число молекул в каждом классе становится меньшим. Поэтому параметры, характеризующие гетероатомы, до сих пор твёрдо не установлены. Параметры в методе Хюккеля заменяют собою сложные интегралы, появляющиеся в любом неэмпирическом расчётном методе. По этой причине лучшие значения параметров зависят от того, какая экспериментально наблюдаемая характеристика исследуется. В целом же, при объяснении строения и свойств сопряжённых систем (ароматических углеводородов, их замещённых, линейных полиенов, радикальных частиц), объяснения их реакционной способности, интерпретации спектров, метод Хюккеля даёт вполне удовлетворительные результаты. По этим причинам, не смотря на развитие более точных полуэмпирических методов и расчётов ab initio, необходимо ознакомиться с методом Хюккеля. Кроме всего прочего, все другие полуэмпирические методы в той или иной степени имеют черты, сходные с методом Хюккеля, и знакомство с ним даёт общее представление о полуэмпирических методах квантовохимических расчётов и может облегчить понимание этих методов. Значение хюккелевской теории прекрасно охарактеризовали Вудворд и Хофман. Они писали, что последние годы «были отмечены плодотворным симбиозом органической химии и теории молекулярных орбиталей. По необходимости это был брачный союз плохой теории с хорошим экспериментом. В руках умных экспериментаторов эти идеи трансформировались в новые молекулы с необычными свойствами». На сегодняшний день в связи с бурным развитием вычислительной техники и широким внедрением более совершенных вычислительных схем квантовой химии метод Хюккеля перестал играть заметную роль в исследовании структуры и свойств органических соединений. На передний план выдвинулись методики, явно учитывающие межэлектронное взаимодействие.

АНТЕННІ ПРИСТРОЇ

ВСТУП

Навчальна дисципліна „Технічна електродинаміка” для студентів спеціальності 6.092400 „Телекомунікаційні системи та мережі” викладається протягом одного семестру, та містить такі розділи:

- основи теорії електромагнітного поля;

- пристрої надвисоких частот;

- антенні пристрої;

- поширення радіохвиль.

Перші два розділи складають модуль 1, а останні два – модуль 2.

Кожен з них є окремою навчальною дисципліною електродинамічного циклу, що вивчається за відповідними виданнями. Засвоїти основні знання та навички із зазначених питань у вказаний термін неможливо без відповідних конспектів лекцій, які узгоджені з робочою навчальною програмою.

Конспекти лекцій для вивчення матеріалу за модулем 1 вже видані декількома накладами видавництвом НАУ. Тому конспект лекцій „Технічна електродинаміка. Модуль 2: Антени та поширення радіохвиль” містить необхідні відомості для вивчення останніх двох із вказаних розділів. У ньому доволі компактно надаються відомості про фізичні принципи випромінювання радіохвиль, їхнього поширення в конкретному середовищі, та прийому відповідними засобами. При цьому використовується у взаємозв’язку та послідовно теоретичний матеріал попередніх розділів дисципліни.

Користування конспектом лекцій „Технічна електродинаміка” дасть можливість отримати первісні знання з принципів дії антен, їх конструкції та характеристик, а також фізичні засади процесів випромінювання радіохвиль, їх поширення в просторі та прийому.