Методы спуска

Большинство итерационных методов, применяемых для решения задач безусловной минимизации функции нескольких переменных, относятся к классу методов спуска. Это такие методы, для которых каждая итерация (шаг) приводит к уменьшению значения целевой функции: f(x_k+1)<f(x_k), для всех k³0.

Структура типичного алгоритма метода спуска для функции двух переменных Q(x,y) состоит в следующем:

1.Задается начальная точка (x₀, y₀), принадлежащая области допустимых значений функции.

2.На текущей k-й итерации (k=0,1, …n) определяется вектор 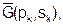задающий направление спуска, причем такой, чтобы для всех достаточно малых значений l>0 (где l- коэффициент, являющийся шагом поиска) выполнялось неравенство:

f(x_k + lp_k, y_k+ ls_k) < f(x_k,y_k).

3.Вычисляется шаг поиска - l_k, для которого выполняется условие п.2, и за очередное приближение к точке минимума принимается точка:

(x_k+ lp_k, y_k+ ls_k), где x_k+ lp_k = x_k+1, аy_k+ ls_k = y_k+1.

4.Проверяется выполнение критерия окончания итераций. Если критерий метода выполняется, то полагают (x*,y*)»(x_k+1,y_k+1). В противном случае осуществляется переход к п.2 и выполняется следующая итерация.

Последовательность точек х₁, х₂, …, х_k,получаемую методом спуска, называют траекторий спуска.

В градиентных методах спуска направление движения к точке минимума целевой функции совпадает с направлением антиградиента, а направление спуска выбирается по формулам:

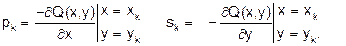
Для использования градиентного метода оптимизации необходимо определить правило выбора шага (l_k) на каждой итерации и правило прекращения итерационного процесса.

При решении вопроса о выборе шага l_k следует учитывать, что выбор малого шага на каждой итерации приведет к малым изменениям аргумента и функции, и, следовательно, к увеличению числа итераций, необходимых для решения задачи. Выбор слишком большого шага l_k может привести не к убыванию целевой функции Q(x,y), а к ее увеличению, и, следовательно, процесс не будет сходиться к точке минимума.

Алгоритм метода градиентного спуска приведен на рис. 1.8.2-1.

По способу выбора шага спуска среди градиентных методов наиболее известными являются метод градиентного спуска с дроблением шага (ГДШ) и метод наискорейшего спуска (НС).