Метод наискорейшего спуска
Суть метода состоит в следующем. Из выбранной точки (x0,y0) спуск осуществляют в направлении антиградиента до тех пор, пока не будет достигнуто минимальное значение целевой функции Q(x, y) вдоль луча (рис.1.8.4-1). В найденной точке луч касается линии уровня. Затем из этой точки спуск проводится в направлении антиградиента (перпендикулярном линии уровня) до тех пор, пока соответствующий луч не коснется в новой точке проходящей через нее линии уровня, и т.д.
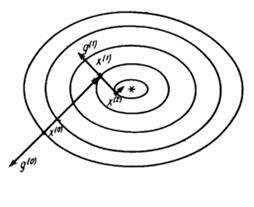
Рис. 1.8.4-1
Выразим целевую функцию Q(x, y) через шаг l. При этом представим целевую функцию на определенном шаге как функцию одной переменной, т.е. величины шага
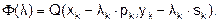
Величина шага на каждой итерации определяется из условия минимума функции 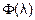 :
:
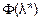 = min(
= min(  (l)) lk = l*(xk, yk), l>0.
(l)) lk = l*(xk, yk), l>0.
Таким образом, на каждой итерации выбор шага lk предполагает решение задачи одномерной оптимизации. По способу решения этой задачи различают:
- аналитический метод (НСА);
- численный метод (НСЧ).
В методе НСА значение шага получают из условия 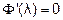 , а в методе НСЧ величину lk находят на отрезке [0;1]c заданной точностью, используя один из методов одномерной оптимизации.
, а в методе НСЧ величину lk находят на отрезке [0;1]c заданной точностью, используя один из методов одномерной оптимизации.
Рис. 1.8.4-2. Алгоритм выбора шага в численном методе наискорейшего спуска НСЧ
с использованием метода золотого сечения
Пример 1.8.4-1. Найти минимум функции Q(x,y)=x2 + 2y2с точностью e=0.1, при начальных условиях: x0=2; y0=1.
Проделаем одну итерацию методом НСА.
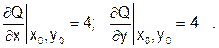 |
Выразим целевую функцию через величину l:
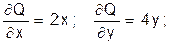 |
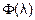 =(x-2lx)2+2(y-4ly) 2 = x2-4lx2+4l2x2+2y2-16ly2+32l2y2.
=(x-2lx)2+2(y-4ly) 2 = x2-4lx2+4l2x2+2y2-16ly2+32l2y2.
Из условия 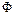 ¢(l)=0 найдем значение l*:
¢(l)=0 найдем значение l*: 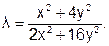
Полученная функция l=l(x,y) позволяет найти значение l. При x=2 и y=1 имеем l=0.3333.
Вычислим значения координат следующей точки:
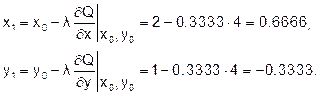
Проверим выполнение критерия окончания итераций при k=1:
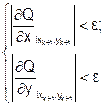
Поскольку |2*0.6666|>0.1 и |-0.3333*4|>0.1 , то условия окончания процесса итераций не выполнены, т.е. минимум не найден. Поэтому следует вычислить новое значение l при x=x1 и y=y1 и получить координаты следующей точки спуска. Вычисления продолжаются до тех пор, пока не выполнятся условия окончания спуска.
Отличие численного метода НС от аналитического состоит в том, что поиск значения l на каждой итерации происходит одним из численных методов одномерной оптимизации (например, методом дихотомии или методом золотого сечения). При этом в качестве интервала неопределенности служит диапазон допустимых значений l - [0;1].
Дата добавления: 2015-03-11; просмотров: 2809;
