И вывод расчетной формулы

Для определения ускорения свободного падения существует несколько способов. Наиболее простыми и надежными являются методы определения ускорения свободного падения с помощью математического маятника. Математическим маятником называется тело, размерами которого можно пренебречь (материальная точка), подвешенное на нерастяжимой и невесомой нити (рис. 5.2).

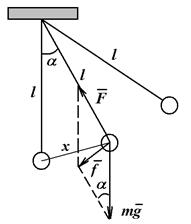
Рис. 5.2.

В настоящей работе используется модель математического маятника, представляющая собой металлический шарик, подвешенный на нити, длину которой можно легко изменять, перемещая вдоль линейки другой конец нити, перекинутой через блок.

Если маятник вывести из положения равновесия на небольшой угол ( 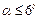), то возвращающая сила, действующая на маятник, будет пропорциональна смещению, поэтому маятник начнет совершать гармонические колебания по закону синуса или косинуса:

х = Аsin(wt+j₀), (5.1)

где х – смещение тела от положения равновесия в момент времени t;

А – максимальное смещение (амплитуда);

w – круговая или циклическая частота колебаний;

j₀ – начальная фаза.

Для получения выражения для расчета ускорения свободного падения с помощью маятника примените к нему второй закон динамики:

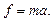(5.2)

Для этого предварительно проделайте следующее.

1. Пользуясь рис. 5.2, выразите силу f, действующую на маятник, когда он проходит произвольное положение, через силу тяжести mg и sin a.

2. Принимая во внимание малость угла a, выразите sin a » a через смещение х и длину маятника l.

3. Учтите, что смещение х и сила f всегда направлены противоположно. В результате должны получить для силы выражение

.

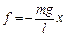4. Найдите выражение для ускорения маятника по формуле

,

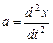т. е. найдите вторую производную функции смещения тела из формулы (5.1).

5. Подставьте значения f и а в формулу (5.2) и произведите преобразования. В результате должны получить:

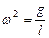. (5.3)

6. Учитывая, что круговая частота w связана с периодом колебаний Т соотношением 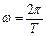, из формулы (5.3) выразите g через Т и l. Получите:

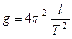. (5.4)

Из формулы (5.4) найдите

.

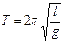Пользуясь выражением (5.4), можно определить ускорение свободного падения. Для этого достаточно опытным путем определить l и Т, но измерение l осложняется тем, что приходится определять положение точки подвеса и центра тяжести маятника. Поэтому Бесселем предложен оригинальный метод, который сводится к следующему. При произвольной длине l₁ измеряется период колебаний Т₁. Затем длина маятника изменяется (изменение длины определяется достаточно просто – линейкой на стене). При длине l₂ соответственно определяется период колебаний Т₂. В результате имеем два уравнения:

, .

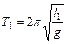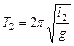Возводя эти уравнения в квадрат и произведя вычитание, получим:

.

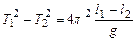Отсюда

,

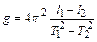или

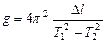. (5.5)

Данное выражение является расчетной формулой для определения ускорения свободного падения методом Бесселя.