ДЕФОРМАЦИЙ

Цель работы:определить модуль упругости (модуль Юнга) для различных материалов.

Приборы и принадлежности: скамья с вертикальными стойками, индикатор, масштабная линейка, образцы исследуемых материалов.

Изучите теоретический материал по одному из учебных пособий [1, гл. II, § 14; 2, гл. V, § 5.2; 4, гл. II, § 10].

При изучении обратите внимание на то, что, несмотря на существование различных видов деформаций тел (одностороннее растяжение или сжатие, всестороннее растяжение или сжатие, кручение, сдвиг, изгиб), все они подчиняются закону Гука, согласно которому сила упругости F_упр, возникающая при малых деформациях любого вида, пропорциональна деформации (смещению) Dх, т. е.

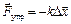, (4.1)

где k – коэффициент упругости.

Знак минус указывает на противоположность направлений силы упругости и смещения.

Необходимо твердо уяснить, что все виды деформаций, в том числе и деформация изгиба, могут быть сведены к деформациям одностороннего сжатия и растяжения. При деформации изгиба стержня одни части его испытывают растяжение, а другие – сжатие (рис. 4.1). Средняя часть стержня почти не оказывает сопротивление изгибу. По этой причине сплошной стержень и трубчатый одинакового диаметра обладают почти одинаковым сопротивлением изгибу.

Обратите внимание на практическое использование этого вывода, а именно, стержни, работающие на изгиб, обычно делают полыми (трубчатыми), чем достигается экономия материала и облегчение конструкций без ущерба их прочности. С такими же явлениями встречаются и в природе: трубчатое строение имеют стебли злаковых растений, кости птиц и др.

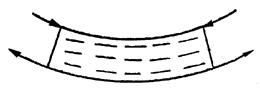
Рис. 4.1.

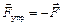Физический смысл модуля Юнга уясните на примере деформации одностороннего растяжения. Пусть к нижнему концу закрепленного стержня длиной l и площадью поперечного сечения S приложена деформирующая сила F. Стержень удлиняется на , и в нем возникает сила упругости F_упр (рис. 4.2). Следует помнить, что при этом , т. е. сила упругости равна по величине, но противоположна по направлению приложенной к телу силе.

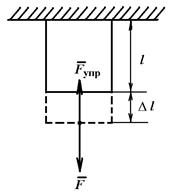
Рис. 4.2.

Опыт показывает, что удлинение стержня пропорционально деформирующей силе, длине стержня и обратно пропорционально площади его поперечного сечения, т. е.

; (4.2)

, (4.3)

где 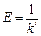– коэффициент, характеризующий упругие свойства ве-

щества стержня. Он называется модулем упругости, или

модулем Юнга.

Физический смысл модуля Юнга заключается в следующем. Из формулы (4.2) следует, что

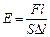. (4.4)

Полагая 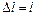и 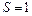, получим:

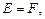
т. е. модуль упругости вещества численно равен силе, растягивающей стержень единичного поперечного сечения в два раза. Измеряется модуль упругости в паскалях (Па).