Спектральный метод.
Статистический метод не дает всех необходимых данных для описания волнения как непрерывного случайного процесса. Более удобен для этих целей спектральный метод, который основан на представлении реального волнения в виде суммы бесконечного числа единичных волн со случайными амплитудами, частотами и фазами, т.е.
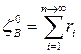 cos (kixi - wit + di) . (2.26)
cos (kixi - wit + di) . (2.26)
Энергия каждой отдельно взятой волны равна
Еi = 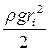 . (2.27)
. (2.27)
В то же время ее можно представить в виде:
Еi = s(wi)Dwi , (2.28)
где s(wi) - удельная энергия, приходящаяся на интервал Dwi, при частоте wi.
Приравнивая (2.27) и (2.28), получим
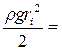 s(wi)Dwi . (2.29)
s(wi)Dwi . (2.29)
Отсюда
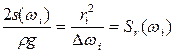 . (2.30)
. (2.30)
Зависимость Sr(w) (рис. 2.3) называется графиком спектральной плотности или энергетическим спектром. Она характеризует распределение энергии волн по амплитудам и частотам.
Связь между спектральными и статистическими характеристиками можно найти из выражения (2.21), подставив в него (2.29),
Dr = 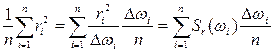 . (2.31)
. (2.31)
При n ® 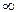
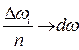 , а сумма становится интегралом.
, а сумма становится интегралом.
Тогда получим
Dr = 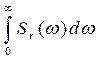 . (2.32)
. (2.32)
С помощью дисперсии уже легко установить связь с высотой волны заданной обеспеченности и с соответствующими баллами волнения.
Спектры чаще всего представляются в форме
Sr (w) = A w-ke-В 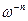 , (2.33)
, (2.33)
где А, В, k, n - параметры, зависящие от условий волнообразования, от степени развитости волнения, от балльности, от акватории и т.д.
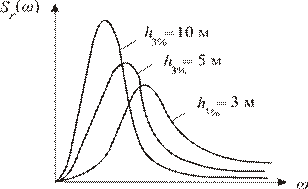
Рис. 2.3. Спектры нерегулярного вол-
нения различной балльности
Обычно спектры нормируют (обезразмеривают), разделив Sr (w) на Dr и умножив на wср, т.е. рассматривают
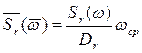 , (2.34)
, (2.34)
где 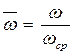 - безразмерная частота;
- безразмерная частота;
wср = 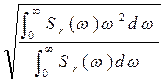 . (2.35) Приближенно wср можно определить графически (рис.2.4), при этом
. (2.35) Приближенно wср можно определить графически (рис.2.4), при этом
wср = 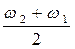 ,
,
где w2 и w1 определяются как границы прямоугольника, у которого площадь равна площади под кривой спектральной плотности, а момент инерции площади относительно оси ординат равен моменту инерции площади под кривой.
Дисперсия при нормировании определяется по формуле (2.24).
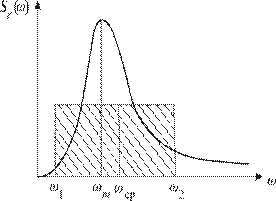
Рис. 2.4. Определение средней частоты спектра
Существует статистическая связь между wср и h3%. Для наиболее употре-бительных спектров
wср = 1,74(h3%)-0,4. (2.36)
Окончательно в нормированном виде спектральная плотность записывается как
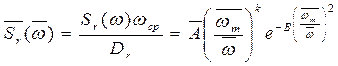 , (2.37)
, (2.37)
где 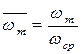 ;
;
wm - частота, соответствующая максимуму спектра (рис. 2.4);
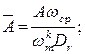
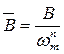 . (2.38)
. (2.38)
Величина wm связана с wср соотношением, зависящим от вида конкретного спектра.
Перечислим некоторые основные спектры:
- спектр Неймана:
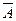 = 33,2; k = 6;
= 33,2; k = 6; 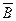 = 3; n =2; wm = 0,707wср;
= 3; n =2; wm = 0,707wср;
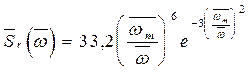 ; (2.39)
; (2.39)
- спектр Бретшнайдера
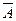 = 7,14; k = 5;
= 7,14; k = 5; 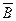 = 1,25; n =4; wm = 0,712wср;
= 1,25; n =4; wm = 0,712wср;
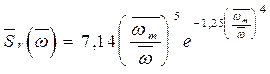 ; (2.40)
; (2.40)
- спектр Вознесенского - Нецветаева (ОСТ по качке)
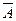 = 9,43; k = 6;
= 9,43; k = 6; 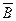 = 1,5; n =4; wm = 0,777wср;
= 1,5; n =4; wm = 0,777wср;
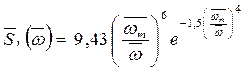 . (2.41)
. (2.41)
Удобство нормированных спектров в том, что они не зависят от балльности волнения.
Дата добавления: 2015-03-11; просмотров: 919;
