Определение неприступного расстояния.

Постановка задачи. Требуется определить расстояние d_АС между двумя точками А и С, отделенными друг от друга препятствием (например, рекой), не допускающим непосредственное измерение мерной лентой или рулеткой (рис. 11.1). При этом требуемая точность или само расстояние не допускают использование оптического дальномера, а светодальномер отсутствует.

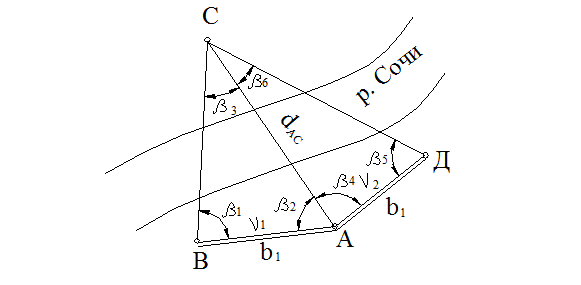
Рис. 11.1. Схема к определению неприступного расстояния.

Решение. От одной из заданных точек (например А, рис. 11.1) разбиваются два базиса: b₁ = AB и b₂ = AД длиной не менее 1/3 d_АС. Точки А, В, С и Д закрепляются на местности кольями и сторожками. Базисы измеряют мерной лентой или рулеткой в прямом и обратном направлении с относительной ошибкой не более 1/2000. В точках А, В, Д измеряют горизонтальные углы b₁, b₂, b₄, b₅ способом приемов. Кроме того, из точки А измеряют углы наклона n₁ и n₂ линий АВ и АД.

Результаты измерений записывают в журнал, аналогичный журналу измерения горизонтальных и вертикальных углов и расстояний теодолитного хода при создании съемочного обоснования тахеометрической съемки.

Вычисляют горизонтальные углы b₃, b₆ по формулам:

b₃ = 180⁰ - (b₁ + b₂), b₆ = 180⁰ - (b₄ + b₅)

и горизонтальные проложения d₁ = b₁ cosn₁ , d₂ = b₂ cosn₂ .

Далее по формулам, следующим из теоремы синусов дважды вычисляют расстояния:

d’_АС = d₁ sinb₂ / sinb₃ ; d’’_АС = d₂ sinb₅ / sinb₆ .

Вычисляют среднее из расстояний d_срАС = ( d’_АС + d’’_АС ) / 2. Проверяют условие: если ( êd’_АС - d’’_АС ê) / d_срАС £ 1/1000, то принимают d_срАС за искомое расстояние d_АС. В противном случае измерения и вычисления повторяют.