Математические модели местности

Математические связи между исходными точками цифровых моделей описываются линейными либо нелинейными (степенными) зависимостями. В первом случае связь между смежными точками модели описывается уравнениями плоскостей, проходящими через каждые три смежные точки модели, во втором – криволинейными поверхностями разного порядка, и, таким образом, рельеф местности задается либо множеством пересекающихся между собой плоскостей, либо поверхностей различной кривизны.

Решение наиболее актуальной задачи при математическом моделировании рельефа и инженерно-геологического строения местности заключается в определении высот (глубин) точек местности, а также уровней воды и соответствующих геологических напластований.

Подавляющее число регулярных и нерегулярных ЦММ предполагают при последующем математическом моделировании линейную интерполяцию высот (глубин) между смежными точками модели.

Задача определения высот точек, уровней воды и поверхностей геологических напластований сводится к нахождению в каждом случае тех трех смежных исходных точек модели, между которыми попадет соответствующая искомая точка, в нахождении коэффициентов уравнения плоскости, проходящей через эти три точки, и, наконец, в определении по полученному уравнению искомой высоты (рис. 10.2).

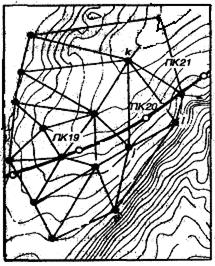
Рис. 10.2. Линейное математическое моделирование рельефа

и инженерно-геологического строения местности.

Если искомая точка (например, 20 – рис. 1.2) попадает между смежными исходными точками ЦММ с номерами i, k и l, то уравнение искомой плоскости в общем виде может быть представлено:

Н = АХ + ВУ + С. (10.3.1)

В уравнении (10.3.1) известны проектные координаты Х и У искомой точки (например, 20 – рис. 10.2), высоту которой нужно определить, но не известны коэффициенты А, В и С уравнения плоскости, проходящей через исходные точки i, k и l цифровой модели.

Если в уравнение (10.3.1) подставить известные координаты трех исходных точек цифровой модели, то получим три уравнения, в которых не известны только три коэффициента А, В и С:

H_j = АX_j + ВY_j + С;

H_k = АX_k + ВY_k + С; (10.3.2)

H_l = АX_l + ВY_l + С.

Система уравнений (10.3.2) решается в матричной форме или методом «прогонки», в результате чего определяют неизвестные коэффициенты А, В и С уравнения (10.3.1), подставив в которое проектные координаты Х и Y искомой точки, определяют ее высоту Н.

Наиболее универсальными являются статистические ЦММ (10.1.6), математическая реализация которых заключается в использовании метода «плавающего квадрата» иди «плавающего круга», в пределах которого строится криволинейная поверхность n - го порядка (рис. 10.3).

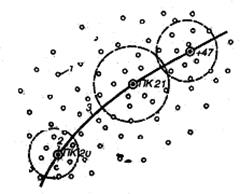
Рис. 10.3. Математическое моделирование рельефа «плавающей» криволинейной поверхностью: 1 – точки статистической ЦММ; 2 – искомые точки; 3 – проектная трасса линейного сооружения.

Наиболее часто для математического моделирования рельефа используются уравнения поверхности 2-го порядка:

Н = АХ² + ВХУ + СY² + DX + ЕY + F, (10.3.3)

где Х, Y - известные проектные координаты точки, высоту которой требуется определить; А, В, С, D, E, F - коэффициенты уравнения аппроксимирующей поверхности 2-го порядка.

Основная идея «плавающей» аппроксимации заключается том, что по аппроксимируемой поверхности от точки к точке перемещается круг или квадрат таким образом, что каждая точка поверхности, высоту которой требуется определить, размещается в его центре (например, точка 21 на рис. 10.3). Радиус круга или размеры стороны квадрата автоматически устанавливаются такими, чтобы в их пределы попало не менее 10 исходных точек модели. Поскольку радиус круга или размеры сторон квадрата меняются с дискретным шагом соответственно ∆r и ∆b, то в пределах выделяемых ими площадей может оказаться и более 10 точек модели (например, 11, 12, 13 и т. д.).

Посколькукоэффициенты А, В, С, D, E, F в аппроксимирующем уравнении (10.3.3) не известны, то для каждой точки модели, попавшей в пределы круга или квадрата, записываются уравнения:

Н_j = АХ²_j + ВХ_jУ_j + СY²_j + DX_j + ЕY_j + F_j;

Н_k = АХ²_k + ВХ_kУ_k + СY²_k + DX_k + ЕY_k + F_k;

……………………………………………… (10.3.4)

Н_n = АХ²_n + ВХ_nУ_n + СY²_n + DX_n + ЕY_n + F_n,

где А, В, С, D, E, F – неизвестные коэффициенты уравнения аппроксимирующей поверхности; H_j, X_j, Y_j,..., Н_n, X_n, Y_n - известные координаты точек модели, попавших в пределы круга или квадрата; n – число точек ЦММ, попавших в пределы круга или квадрата.

Поскольку число неизвестных в системе (10.3.4) меньше числа уравнений (которых не менее 10), то система решается методом «наименьших квадратов». Таким образом, определяют неизвестные коэффициенты аппроксимирующего уравнения (10.3.3), подставив в которое известные проектные координаты Х и Y точки (например, 21), определяют ее высоту или глубину Н.

Далее круг или квадрат перемещают в центр очередной искомой точки, и процедура повторяется. При этом если плотность исходных точек модели в районе очередной определяемой точки уменьшилась, то размеры круга или квадрата автоматически возрастут, а если плотность возросла — то наоборот уменьшатся.

Для математического описания ситуационных, почвенно - грунтовых, гидрогеологических и других условий местности используют контурную индексацию объектов местности с перечнем номеров точек вдоль каждого такого контура (урез воды, подошва подводной части пляжа, газопровод и т. д.). Для замкнутых контуров (здания, причалы, волноломы и т. д.) точки замыкания повторяются.