Определение формы и размеров Земли. Триангуляция.

Земля имеет форму близкую к сферической. Об этом знали различные древние народы. В частности, многие греческие философы не имели в этом сомнения, начиная с древнейших. Уже Пифагор в VI веке до н.э. учил, что Земля шарообразна и вращается вокруг центрального огня.

Истинные размеры Земли были известны древним халдеям и египтянам. К сожалению, до нас не дошли методы, которыми были получены эти значения. Самые ранние, из известных, измерения размеров Земли провёл Эратосфен (276—194 гг. до н. э.). Он определил, что в эпоху летнего солнцестояния зенитное расстояние Солнца в полдень в Александрии равно 7°,2, в то время как в Сиене Солнце в это момент находилось точно в зените. Зная, что Сиена находится на одном меридиане с Александрией, он решил, что расстояние между этими городами и равно 7°,2 окружности Земли. Это расстояние было хорошо известно в греческих стадиях, так как они лежали на оживленном торговом пути. Подставив с свои расчеты полученное значение, Эратосфен вычислил длину земной окружности равную 250 000 стадий. Отсюда следовало, что радиус Земли равен (в современных единицах) 6300 км.

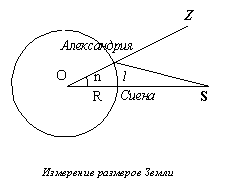Эти расчеты можно представить таким образом. Представим, что l - длина дуги меридиана, а n - ее значение в градусной мере. Тогда длина дуги 1° меридиана l₀ будет равным

.

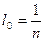Длина всей окружности меридиана равна

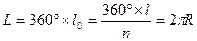, откуда получаем радиус окружности Земли

.

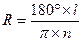Значение .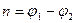

Здесь j₁ и j₂ - географические широты городов.

Впервые расстояние от Земли до Солнца астрономическими методами установил Аристарх Самосский. Измеряя угловое расстояние Луны от Солнца в момент первой четверти, когда угол Земля-Луна-Солнце равен 90°, он нашел, что "расстояние от Земли до Солнца превышает расстояние до Луны более чем в 18, но менее чем в 20 раз..., что такое же отношение имеет диаметр Солнца к диа­метру Луны: что диаметр Солнца к диаметру Земли имеет отно­шение большее, чем 19 к 3, но меньшее, чем 43 к б...". Если разобраться в этих соотношениях, то получается, что радиус Солнца составляет около семи радиусов Земли. Именно это и привело Аристарха Самосского к выводу, что не Земля, а Солнце, как большее тело, расположено в центре мира. Конечно, значения, полученные греческим учёным, не соответствуют действительности, но показывают правильную тенденцию. Метод Аристарха Самосского в принципе верен, однако плохая точность измерений углов не позволила ему получить верные результаты.

Многочисленные современные измерения на земной поверхности показали, что длина одного градуса земного меридиана отличается на разных широтах. Возле экватора это значение равно 110, 6 км, а возле полюсов 111,7 км. Длина одной минуты среднего градуса широты равна 1852,2 м. Она принимается за основу морских измерений и носит название морской мили. Ею пользуются в морском деле, где все расчеты принято вести в гра­дусах, минутах и секундах. Известны также сухопутная миля, равная 1609 м, миля географи­ческая, равная 4 мин широты или 7412,6 м, и дру­гие мили. Диаметр Земли между полюсами с севера на юг (длина земной оси) равен 12 713,7 км. Диаметр земного экватора равен 12756,5 км.

Кривизна земной поверхности меньше в полярных областях, чем в экваториальных. Это свидетельствует о том, что Земля имеет поверхность близкую к сфероиду.

По измерениям элементов земного сфероида Международным астрономическим союзом в 1964 г. было принято, что его малая полуось, совпадающая с осью вращения b = 6356,78 км, а большая полуось, лежащая в плоскости экватора а = 6378,16 км. Сжатие e = (a - b)/a = 1/298,25.

Реальная фигура Земли, имеющая горы, впадины, моря и др. неровности рельефа, не может быть описана не одним правильным геометрическим телом. Сегодня фигура Земли называется геоидом. Изучением формы нашей планеты занимаются геодезия и гравиметрия.

Метод триангуляции впервые был применен Снеллиусом в 1615 г. при измерении дуги меридиана в Голландии. С тех пор и до настоящего времени в разных странах, на разных широтах было измерено много дуг на поверхности Земли и не только по меридианам, но и по параллелям. Все эти измерения показали, что длина дуги 1° меридиана не одинакова под разными широ­тами: около экватора она равна 110,6 км, а около полюсов— 111,7 км, т. е. увеличивается к полюсам. Это означает, что кривизна земной поверхности меньше в полярных областях. чем в экваториальных. Следовательно, Земля отличается от шара и имеет несколько сплющенную форму, близкую к сфе­роиду (эллипсоиду вращения.),

Большие расстояния на земной поверхности измерить очень трудно. Этому мешают неровности формы земного ландшафта. Вычисления проводятся с помощью специального метода - триангуляции, который требует измерения небольшого базиса и углов. Впервые он был применен Снеллиусом в 1615 году при измерении меридиана в Голландии.

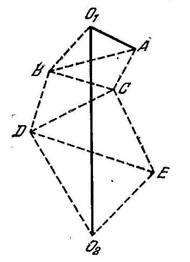Суть метода триангуляции заключается в следующем. По обе стороны дуги 0₁0₂, длину которой необходимо определить, выбирается несколько точек A,B,C,D,E… на рас­стояниях примерно 40 км одна от другой. Точки выбираются так, чтобы из каждой были видны хотя бы две другие точки. Во всех точках устанавливаются геодезические вышки. Наверху вышки делается площадка для наблюдателя. Расстояние между двумя соседними точками, например, О₁А, выбирается на очень ровной поверхности и принимается за базис. Длину базиса измеряют очень точно с помощью мерной ленты. После этого наблюдатель на каждой вышке измеряет все углы треугольников О₁АВ, АВС, BCD, ... Зная в первом треугольнике 0₁АВ все углы и базис, можно вычислить и две другие его сто­роны 0₁В и АВ, а зная сторону АВ и все углы треугольника АВС, можно вычислить стороны АС и ВС и т. д. Таким образом, шаг за шагом, можно вычислить длину ломаной линии O₁BDO₂. Определив из точки O₁ азимут направления стороны О₁А, нужно спроецировать ломаную линию 0₁ВDО₂ на ме­ридиан O₁O₂ иполучить линейные размеры дуги O₁O_2.