Приложение 3. Дифференциальные уравнения первого порядка.
| Уравнения с разделяющимися переменными | Уравнения, однородные относительно переменных | Уравнения в полных дифференциалах | Линейные дифференциальные уравнения |
| y' = f(x)g(x) | y' = f(x,y), где f(x,y) – однородная функция нулевого порядка | M(x,y)dx+N(x,y)dy= 0, где
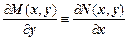
| y' + P(x)y = Q(x) |
1. 
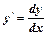2. Разделить переменные.
3. Проинтегрировать.
| 1. Замена 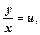 где
u=u(x).
2. После замены получим уравнение с разделяющимися переменными.
3. Решив его, делаем обратную замену.
| 1. Проверяем
 .
2. Решением дифференциального уравнения является u=u(x), где
| 1. y' + P(x)y = 0 – линейное дифференциальное уравнение с разделяющимися переменными. 2. y' + P(x)y = Q(x) а) метод вариации произвольной постоянной. б) метод Бернулли. |
Литература
- Высшая математика для экономистов / Под ред. Н.Ш. Кремера.
3-е изд. М.: Высшее образование, 2008. - Высшая математика для экономистов: Учеб. пособие для вузов. Серия «Высшее образование». Ростов н/Д: Феникс, 2004.
- Высшая математика для экономических специальностей: Учебник и практикум / Под ред. Н.Ш. Кремера. М.: Высшее образование, 2005.
- Высшая математика. Общий курс / Под ред. А.И. Яблонского. Минск: Высшая школа, 1993.
- Грес П.В. Математика для гуманитариев: Учебник для вузов / Рек. Мин. обр. М.: Логос, 2003.
- Гусакова В.И. Шепелова Н.С. Математика: Учебно-метод. пособие. Ростов н/Д: СКАГС, 2008.
- Гусакова В.И., Кривошлыков В.Н., Шепелова Н.С. Математика: Методические указания для самостоятельной работы студентов. Учеб.-метод. пособие. Ростов н/Д: СКАГС, 2010.
- Красс М.С., Чупрынов Б.П. Математика для экономистов. СПб: Питер, 2009.
- Математика и информатика: Учеб. пособие для вузов / Под ред. В.Д. Будаева. М.: Высшая школа, 2004.
- Тугуз Ю.Р. Математика. Ч.1. Математический анализ и линейная алгебра. Ростов н/Д: СКАГС, 2005.
| |
Учебное издание
Гусакова Валентина Ивановна,
Дата добавления: 2014-12-16; просмотров: 909;