Разложение функций в ряд Тейлора.

При исследовании свойств бесконечно дифференцируемых функций изучают их степенные ряды – ряды Тейлора.

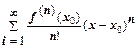Пусть функция f(x) определена в некоторой окрестности точки x₀ и имеет в этой точке производные всех порядков.

Ряд

называется рядом Тейлора для функции f(x) в точке x₀.

Функция f(x) может быть разложена в степенной ряд на интервале (x₀ -R, x₀+R) , если существует степенной ряд, сходящийся к f(x) на этом интервале. Если функция раскладывается в степенной ряд в некоторой окрестности точки x0, то это ряд Тейлора.

Пусть функция f(x) бесконечно дифференцируема на интервале (x₀-R,x₀+R), и все её производные ограничены в совокупности на этом интервале, то есть существует число M>0 , такое, что для всех 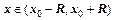и для всех n=1,2… справедливо неравенство 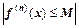, тогда ряд Тейлора сходится к f(x) для всех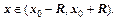

Приведем разложения в ряд Тейлора для основных элементарных функций.

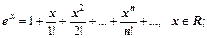
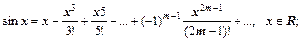
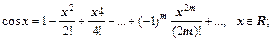
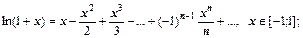
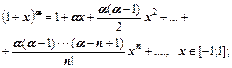
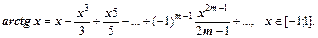
Пример 1. Разложить функцию 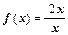в ряд по степеням x. Найти область сходимости ряда.

Р е ш е н и е. Используем разложение:

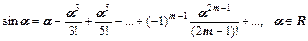
Данный ряд сходится при любом значении α. В данном случае α =2x, 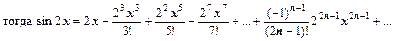и

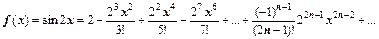
Область сходимости ряда: .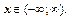

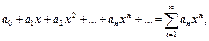Теорема Абеля. Если степенной ряд

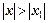
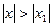сходится при x = x₁ , то он сходится абсолютно для всех

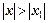Следствие. Если при х = х₁ ряд расходится, то он расходится для всех

.

Пример 2. Найти область сходимости ряда

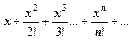
Р е ш е н и е. Находим радиус сходимости:

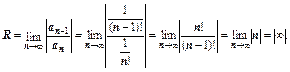
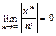Следовательно, данный ряд сходится при любом значении х. Общий член этого ряда стремится к нулю, т.е. .