Между явлениями
Как известно, в природе все взаимосвязано и взаимообусловлено. Изменчивость одного признака какого-либо явления находится в некотором соответствии с изменчивостью другого.
Если изменению одного признака всегда соответствует строго определенное изменение второго, говорят о функциональной зависимости (связи). Примером такой зависимости служат физические и химические явления (закон Бойля-Мариотта), зависимость в геометрии (длины окружности и площади круга от величины радиуса) и т.д.
Когда с изменением одного признака второй может измениться на величину, которую заранее предопределить невозможно, и когда каждому значению одного признака может соответствовать несколько значений другого признака, говорят о корреляционной связи.
Корреляционная зависимость различается по форме связи, ее направлению и силе.
Форма связи может быть прямолинейной и криволинейной. Прямолинейная связь характеризует равномерные изменения одного признака в соответствии с равномерными изменениями второго признака при незначительных отклонениях. При криволинейной связи равномерным изменениям одного признака соответствуют неравномерные, но закономерные изменения второго признака. Если форму связи изобразить графически, то прямолинейная связь будет выглядеть в виде прямой, а при криволинейной связи общая тенденция зависимости одного признака от другого в определенном месте изменяет свое направление, дает изгиб.
Направление связи может быть прямое (положительное) или обратное (отрицательное). Прямая связь характеризуется увеличением (уменьшением) одного признака при увеличении (уменьшении) другого. Например, при снижении заболеваемости снижается и смертность. При обратной связи с увеличением (уменьшением) одного признака второй, наоборот, уменьшается (увеличивается). Например, с увеличением охвата населения вакцинацией заболеваемость инфекционными болезнями снижается.
Сила связи позволяет судить о степени корреляции, тесноте связи, под которыми понимается степень сопряженности связанных признаков. Одним из способов измерения связи является вычисление коэффициента корреляции. Коэффициент корреляции может принимать любое значение в пределах от (–1) до (+1). Коэффициент корреляции, равный 0, говорит о полном отсутствии связи. Чем ближе размер коэффициента к (+1) или к (–1), тем соответственно больше измеряемая им прямая или обратная связь.
Оценка размеров корреляции может производиться по следующей схеме (табл.7).
Таблица 7.
Схема оценки коэффициента корреляции
| оценка корреляции | величина коэффициента корреляции при наличии | ||
| прямой связи | обратной связи | ||
| малая (слабая) | 0-0,29 | 0 – (– 0,29) | |
| средняя (умеренная) | 0,3-0,69 | (– 0,3) – (– 0,69) | |
| большая (сильная) | 0,7-1,0 | (– 0,7) – (–1,0) | |
Коэффициент корреляции вычисляется по формуле:
rxy= 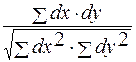 .
.
В этой формуле rxy обозначает коэффициент корреляции, x и y – коррелируемые ряды, dx и dy − отклонения каждого из чисел этих рядов от средних. Число парных членов в коррелируемых рядах обозначается n.
Приведем пример вычисления коэффициента корреляции.
Пример17. В связи с прогнозируемой эпидемией гриппа в школах города провели вакцинацию детей против гриппа. По ряду причин численность вакцинированных детей в различных школах значительно варьировала. Заболеваемость гриппом в ходе последующей эпидемии гриппа среди детей школ города также заметно различалась. Можно ли в качестве причины различий заболеваемости детей гриппом в различных школах предположить разную степень охвата учащихся вакцинацией? Чтобы ответить на данный вопрос, определим степень связи между этими явлениями путем расчета и оценки коэффициента корреляции (табл.8).
Полученная величина коэффициента корреляции rxy =(–0,98) свидетельствует о наличии сильной обратной связи между показателями привитости школьников противогриппозной вакциной и их заболеваемостью гриппом во время эпидемии, следовательно, можно предположить, что причиной различий в заболеваемости детей гриппом во время эпидемии является разная степень охвата учащихся вакцинацией.
Таблица 8.
Дата добавления: 2014-12-16; просмотров: 849;
