Прямая на плоскости. 1.38. Составить уравнение прямой, проходящей через точку А, параллельно: 1) оси ОУ, А(2; –3); 2) оси ОХ
1.38. Составить уравнение прямой, проходящей через точку А, параллельно: 1) оси ОУ, А(2; –3); 2) оси ОХ, А(1; 2); 3) прямой 2x – 3y + 1 = 0, А(2; –3); 4) прямой x + y – 2 = 0, А(1; 2).
1.39. Составить уравнение прямой, проходящей через точку А, перпендикулярно прямой: 1) 3х – 2у + 5 = 0, А (2; –1); 2) 2х + у – 7 = 0, А(0; 3).
Задача про треугольник
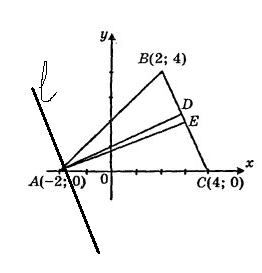
Треугольник задан координатами своих вершин А(–2; 0), В(2; 4), С(4; 0). Найти: 1) уравнение стороны; 2) уравнение медианы, проведенной из вершины А; 3) уравнение высоты, проведенной из вершины А; 4) уравнение прямой, проходящей через А параллельно ВС.
1)  Найдем уравнение стороны ВС по формуле уравнения прямой, проходящей через две заданные точки:
Найдем уравнение стороны ВС по формуле уравнения прямой, проходящей через две заданные точки:
 (1.1)
(1.1)
В(2; 4), С(4; 0), следовательно,
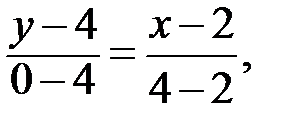
2у – 8 = –4х + 8,
2у = –4х + 16,
у = –2х + 8.
Рис. 1.3. Треугольник на плоскости
2) Найдем уравнение медианы АЕ из точки А:
Пусть Е – середина отрезка ВС. Координаты середины отрезка найдем по формулам:
Хсер = 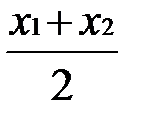 , Усер =
, Усер = 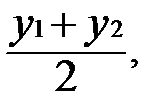
ХЕ = 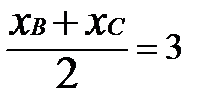 , УЕ =
, УЕ = 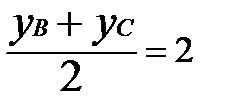 .
.
Точка Е имеет координаты Е(3; 2). Найдем уравнение прямой (АЕ) по (1.1): 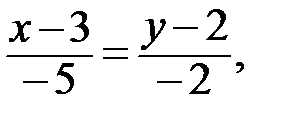
–2х + 6 = – 5у + 10, 5y = 2x+4, у = 0,4 х + 0,8 –уравнение медианы.
3) Найдем уравнение высоты АD.
Т. к. прямая AD перпендикулярна прямой ВС, то из условия перпендикулярности прямых через угловые коэффициенты имеем:
kАD= 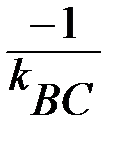 =
= 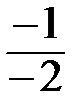 =
= 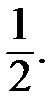
Уравнение прямой, проходящей через данную точку с известным угловым коэффициентом, имеет вид:
у – у0 = k (х – х0) (1.2)
Используя точку А(–2; 0) и k = 1/2, имеем у – 0 = 0,5(х – (–2)) или
у = 0,5х + 1 –уравнение высоты.
4) Найдем уравнение прямой, проходящей через точку А и параллельной прямой ВС.
Т. к. прямая l // BC, то их угловые коэффициенты равны kι = kВС.
kι = –2. Тогда по уравнению (1.2), зная точку А(–2; 0) и k = –2, найдем
у – 0 = – 2 (х + 2) или у = –2х – 4 –уравнение параллельной прямой.
Все уравнения полученных прямых проверьте по чертежу! Свободный член в уравнении прямой показывает её пересечение с осью ОУ.
1.40. Для треугольников, заданных координатами своих вершин найти 1) уравнение сторон; 2) уравнение медиан; 3) уравнение высот 4) уравнение прямой, проходящей через вершину, параллельно противоположной стороне, 5) угол А треугольника.
1) А(1; 1), В(2; 5), С(6; 2); 2) А(–1;–1), В(2; 5), С(4; –2);
3) А(–3; 1), В(2; 4), С(3; –1); 4) А(1;–2), В(6; 2), С(–1; 6);
5) А(–2; 3), В(4; 5), С(4; –2); 6) А(1;–3), В(3; 4), С(7; –2);
7) А(1; 3), В(8; 5), С(3; –2); 8) А(–4;–2), В(1; 5), С(3; –2);
9) А(–5; –1), В(–4; 6), С(1; 0); 10) А(1; 1), В(2; 2), С(3; –4).
1.41. А – вершина прямоугольника, противоположный угол образован осями координат. Составить уравнения сторон и диагоналей этого прямоугольника, если: 1) А (–4; 3); 2) А (2; 3).
1.42. Составить уравнение прямой, отсекающей на осях координат OX и OY отрезки: 1) а = 2 и b = –5; 2) а = –1 и b = 4.
1.43. Найти уравнение прямой, проходящей через точку А (4; 3) и отсекающей от координатного угла треугольник площадью 3 кв. ед.
1.44. Составить уравнение прямой, проходящей через точку пересечения прямых 5х – у +10 = 0 и 8х + 4у + 9 = 0 параллельно прямой х + 3у = 0.
1.45. Составить уравнение прямой, проходящей через точку пересечения прямых 2х – 3у + 5 = 0 и 3х + у – 7 = 0, перпендикулярно к прямой у = 2х.
1.46. Даны вершины параллелограмма: точки А(3; –5), В(–1, 3). Определить четвертую вершину D, противоположную В.
1.47. Известны уравнения двух смежных сторон параллелограмма
х + у + 5 = 0 и х – 4у = 0. Составить уравнения двух других сторон, если известна точка пересечения его диагоналей Р(2; –2).
1.48. Известны середины сторон треугольника АВС, это точки Р(1; 2),
Q(5;–1) и R(–4; 3). Составить уравнение его сторон.
1.49. Известны одна из вершин А(–2; 1) и уравнения двух сторон прямоугольника 3 х – 4у + 5 = 0и 4х + 3у – 7 = 0. Составить уравнения двух других сторон.
Дата добавления: 2014-12-14; просмотров: 1453;
