Глава 2. Прямая

Поскольку положение прямой в пространстве однозначно определяется двумя точками, то и для определения положения проекций прямой также достаточно зафиксировать проекции двух точек. Поэтому для построения проекций прямой можно использовать все правила, касающиеся проецирования точки.

2.1. Прямые частного и общего положения

2.1.1. Прямые уровня

Прямой уровня называется прямая, параллельная одной из плоскостей проекций. Поскольку плоскостей проекций три, то и прямых уровня тоже три.

Исходя из положения прямых уровня в пространстве, их проекции выглядят как показано на рис. 2.1.

а)Прямая, параллельная горизонтальной плоскости проекций П₁, называется горизонтальной прямой уровня или горизонталью и обозначается h.

б) Прямая, параллельная фронтальной плоскости проекций П₂, называется фронтальной прямой уровня или фронталью и обозначается f.

в) Прямая, параллельная профильной плоскости проекций П₃, называется профильной линией уровня и обозначается p.

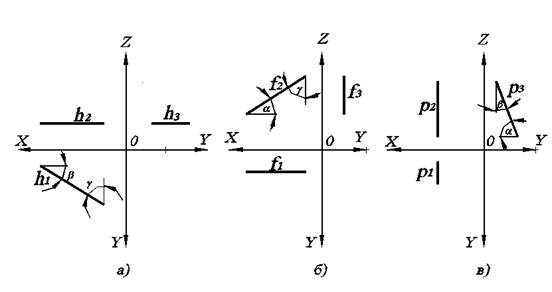
Рис. 2.1. Линии уровня на комплексном чертеже: а) горизонтальная; б) фронтальная; в) профильная.

Горизонталь характерна тем, что ее фронтальная проекция параллельна оси ОХ. Фронталь характерна тем, что ее горизонтальная проекция параллельна оси ОХ.

Очевидно, что если прямая параллельна какой-либо плоскости, то на эту плоскость она проецируется в натуральную величину (без искажений). Поэтому h₁, f₂, p₃ – это натуральная величина соответствующих прямых h, f, p.

a - угол наклона прямой уровня к П₁,

b - угол наклона прямой уровня к П₂,

g - угол наклона прямой уровня к П₃.

2.1.2. Проецирующие прямые

Проецирующей прямой называется прямая перпендикулярная одной из плоскостей проекций, а следовательно, параллельная двум другим плоскостям проекций.

Исходя из положения проецирующих прямых в пространстве, их проекции выглядят как показано на рис. 2.2.

а)Прямая, перпендикулярная горизонтальной плоскости проекций П₁, называется горизонтально-проецирующей прямой и обозначается i.

б)Прямая, перпендикулярная фронтальной плоскости проекций П₂, называется фронтально-проецирующей прямой и обозначается j.

в)Прямая, перпендикулярная профильной плоскости проекций П₃, называется профильно-проецирующей прямой обозначается r.

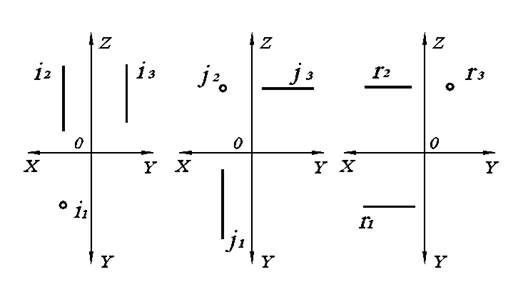
Рис. 2.2. Проецирующие прямые на комплексном чертеже: а) горизонтально-проецирующая; б) фронтально-проецирующая; в) профильно–проецирующая.

У проецирующих прямых две проекции параллельны плоскостям проекций. Поэтому i₂, i₃, j₁, j₃, r₁, r₂ – это натуральные величины соответствующих прямых i, j, r.

2.1.3. Прямая общего положения

Прямой общего положения называется прямая, занимающая общее положение в пространстве, т.е. не параллельная ни к одной из плоскостей проекций, а следовательно, расположенная к каждой из них под углом.

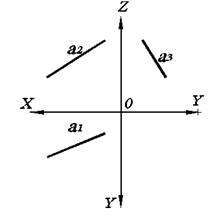
Рис. 2.3. Прямая общего положения на комплексном чертеже.

Естественно, что ни одна из проекций прямой общего положения не показывает ее натуральную величину, а также угол наклона к одной из плоскостей проекций (рис. 2.3).

2.2. Определение натуральной величины отрезка прямой и углов наклона его к плоскостям проекций методом прямоугольного треугольника

Одним из методов определения натуральной величины отрезка прямой является метод прямоугольного треугольника, который можно сформулировать так: натуральной величиной отрезка является гипотенуза прямоугольного треугольника, одним из катетов которого служит горизонтальная (фронтальная) проекция отрезка, другим – разность расстояний от граничных точек фронтальной (горизонтальной) проекции отрезка до оси ОХ. При этом углом наклона отрезка к горизонтальной (фронтальной) плоскости проекции является угол между гипотенузой прямоугольного треугольника и горизонтальной (фронтальной) проекцией отрезка.

В соответствии с этим построения необходимо выполнять в следующей последовательности. Из любой точки (например, D₁) отрезка С₁D₁ проведем перпендикуляр к нему (рис. 2.4.).

На нем, отложив отрезок длиной Dz, получим точку D*. После соединения точек D* и С₁ получаем прямоугольный треугольник С₁D₁D*, в котором С₁D* - натуральная величина отрезка СD, a - угол наклона отрезка СD к плоскости П₁. Для определения угла наклона к плоскости П₂ проведем аналогичные построения на фронтальной проекции.

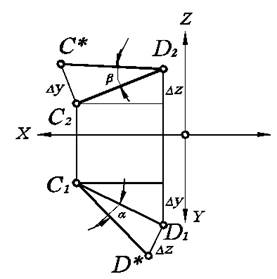
Рис. 2.4. Определение натуральной величины отрезка прямой способом прямоугольного треугольника.

2.3. Взаимное положение прямых в пространстве. Конкурирующие точки

Прямые в пространстве могут занимать по отношению друг к другу одно из трех положений: а) быть параллельными; б) пересекаться; в) скрещиваться, т.е. не пересекаться, но и не быть параллельными. Рассмотрим на рис. 2.5 как при этом располагаются их проекции. Поскольку профильные проекции прямых можно построить по двум имеющимся, то на рис. 2.5 ограничимся двухкартинным комплексным чертежом.

В соответствии с одним из свойств ортогонального проецирования, если прямые параллельны, то их одноименные проекции параллельны (рис. 2.5а). Если прямые пересекаются, то их проекции пересекаются, причем точки пересечения проекций лежат на одной линии проекционной связи (А – точка пересечения прямых с и d). Если прямые скрещиваются, то их проекции пересекаются, но точки пересечения проекций не лежат на одной линии проекционной связи (на рис. 2.5в точки С₁ и В₂) не лежат на одной линии проекционной связи. Тогда, следуя по вертикальной линии связи от точки С₁, получим на каждой из прямых n₂ и m₂ соответственно две проекции: точки С₂ и другой точки D₂, а следовательно, на пересечении n₁ и m₁ лежат две точки С₁ и D₁, слившиеся в одну.

Точки, лежащие на одном проецирующем луче, называются конкурирующими.. Точки, горизонтальные проекции которых совпадают, называются горизонтально–конкурирующими (на рис. 2.5в см. точки C и D), а если совпадают фронтальные проекции, то точки называются фронтально-конкурирующими (на рис. 2.5в - точки В и Е).

При этом конкурирующие точки расположены на разном расстоянии от плоскостей проекций. Фронтально-конкурирующая точка, расположенная ближе к П₂, будет закрыта от наблюдателя точкой, расположенной дальше от П₂, а следовательно, ближе к наблюдателю. Значит, ее горизонтальная проекция расположена дальше от ОХ. Тогда в нашем примере точка Е – видимая, а точка В – невидимая. Аналогично С – видимая , а D – невидимая. Таким образом, видимой является точка, у которой проекция расположена дальше от оси ОХ. Чтобы различать точки на чертеже, невидимую заключают в круглые скобки.

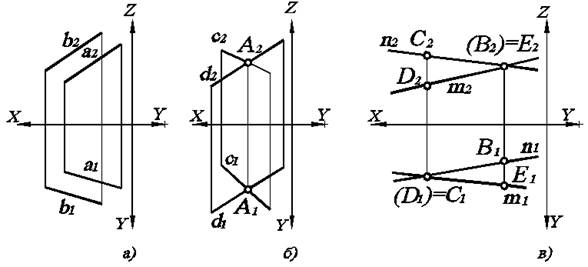
Рис. 2.5. Двухкартинный комплексный чертеж прямых, занимающих по отношению друг к другу следующее положение: а) а êêb; б) с Ç d; в) n ¸ m

Вопросы для самоконтроля

1. Что называется прямой общего положения?

2. Какая прямая называется прямой уровня?

3. Какая прямая называется проецирующей прямой?

4. Какое положение прямые могут занимать в пространстве по отношению друг к другу?

5. Как определить натуральную величину отрезка прямой по ее комплексному чертежу?