Задания для самостоятельной работы. I. Ответьте на следующие вопросы по теории:

I. Ответьте на следующие вопросы по теории:

1) Что называется факториалом?

2) Что называется перестановками? Написать формулу вычисления.

3) Что называется перестановками? Написать формулу вычисления.

4) Что называется сочетанием из n элементов по m? Написать формулу вычисления.

5) Что называется размещением из n элементов по m? Написать формулу вычисления.

6) Написать формулу вычисления вероятности события.

7) Написать формулу вычисления условной вероятности.

8) Написать формулу вычисления полной вероятности.

9) Написать формулу Байеса.

10) Что называется дискретной случайной величиной?

11) Что называется законом распределения дискретной случайной величины?

12) Написать формулу вычисления математического ожидания дискретной случайной величины.

13) Написать формулу вычисления дисперсии дискретной случайной величины.

14) Написать формулу Бернулли.

15) Охарактеризовать распределение Пуассона и записать применяемые формулы.

II. Решите самостоятельно следующие задания.

1. В урне 12 билетов. Из них 3 выигрышных. Какова вероятность того, что первый вынутый билет окажется выигрышным?

2. Три стрелка стреляют по мишени. Предполагается, что события попадания в мишень для стрелков независимы и вероятности попадания стрелков в мишень равны 0,4, 0,3, 0,2.

Какова вероятность того, что:

• Все три выстрела окажутся успешными;
• Хотя бы один из выстрелов окажется успешным;
• Один выстрел окажется успешным, два неуспешными.

3. M% всех мужчин и N% всех женщин –дальтоники. Наугад выбранное лицо оказалось дальтоником. Какова вероятность того, что это мужчина? Число мужчин и женщин считается одинаковым.

4. Случайная величина X задана рядом распределения.

Найти математическое ожидание MX и дисперсию DX.

5. Количество Х принимаемых за час звонков по домашнему телефону имеет распределение Пуассона. Среднее количество принимаемых за час звонков λ = 8. Какова вероятность того, что будет принято за час точно 3 звонка? Более 2?

6. Количество отказов прибора в течение 10000 часов имеет распределение Пуассона с параметром λ = 1. Какова вероятность того, что прибор в течение 10000 часов проработает безотказно?

7. Идёт охота на волка. В охоте участвуют 4 охотника. Н_i – событие – волк вышел на i-го охотника, i = 1,2,3,4. Р(Н₁) = 0,6; Р(Н₂) = 0,2; Р(Н₃) = Р(Н₄) = 0,1.

8. Вероятность убийства волка i-ым охотником - 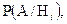если волк вышел на него. P(A/H₁) = 0,9; P(A/H₂) = 0,8; P(A/H₃) = 0,7; P(A/H₄) = 0,6.

Известно, что волк был убит. Какова вероятность того, что волк убит первым охотником?

9. Имеются три завода по производству телевизоров. Первый завод выпускает 60% продукции, второй завод – 10% продукции, третий завод – 20% продукции. У первого завода 10% брака, у второго – 5% брака, у третьего – 3% брака. Купленный в магазине телевизор оказался бракованным. Какова вероятность того, что бракованный телевизор произведен первым заводом?

10. Функция распределения F(x) непрерывной случайной величины равна 0 при x < 0; x³ при 0 ≤ x ≤ 1; 1 при х > 1. Найти математическое ожидание МХ, дисперсию DX, P(0 < X < 0,1).