Статика, нахождение стационарного решения

С течением времени в такой системе происходят процессы взаимного превращения одной противоположности в другую и обратно, что в итоге приводит ее в состояние равновесия или гомеостаза.

На рис.2.1 показан граф перехода из одной противоположности в другую.

l

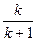P (А ) = , где .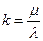

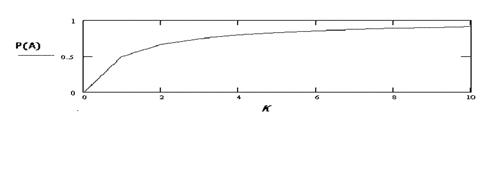
Рис.2.2

На рис. 2.2 показана зависимость P (A) от k, из которой можно сделать следующие выводы:

1. Противоположность A исчезает, когда нет обратного преобразования (m = 0 или “ любовь исчезает – остается одна ненависть”).

2. При любом k>0 P (A) ¹1, т.е. строго говоря, P (A) приближается к единице, но никогда ее не достигает. Следовательно, в системе возникает смесь двух противоположностей (A Ú Ā), что подтверждается и в природных системах: между зимой и летом - весна, между летом и зимой – осень, между любовью и ненавистью – дружба, между симпатией и антипатией - равнодушие и т. д.

Таким образом, возникает предложение в амбивалентную систему ввести третье состояние, а именно, состояние смеси.

На рис.2.3 показан граф переходов в такой системе.

	l		l

		m,		m,

Рис. 2.3

Для такой системы уравнения Колмогорова имеют следующий вид:

P¢(A)_t = - l P (A)_{t +} m P(AÚ Ā )_t

P¢(AÚĀ)_t = -( l+m ) P (AÚ Ā )_t + l P (A)_t + m P(Ā)_t

P¢(Ā)_t = -m P (Ā)_t + l P (AÚ Ā )_t

P(A)_t + P (AÚ Ā )_t+ P(Ā)_t = 1 P (A)₀ = 1.

Для установившегося режима (гомеостаза) приP¢(A)_t=P¢(AÚĀ)_t=P¢(Ā)_t=0 получаем систему алгебраических уравнений, решение которых дает следующие выражения для вероятностей существования двух противоположностей A, Āи их смеси AÚĀ:

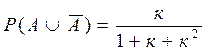
На рис. 2.4 показаны зависимости вероятностей P(A ), P(Ā ) и P (AÚ Ā) от параметра k,

Рис. 2.4

Обращает на себя внимание тот факт, что максимальное значение вероятности существования смеси двух противоположностей, равное 1/3, достигается при l=m, что вполне объяснимо. Анализ этих зависимостей показывает, что, изменяя соотношение между интенсивностями перехода, т.е. усиливая или ослабляя одну из противоположностей, можно управлять гомеостазом бинарной системы.

На рис.2.5 показаны графики зависимостей вероятностей P(A ), P (AÚ Ā) и P(Ā ) от времени.

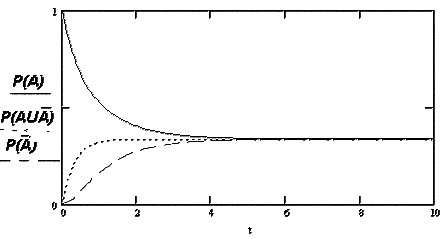
Рис.2.5

С практической точки зрения, конечно, представляет интерес состояние гомеостаза, при котором система проявляет живучесть и сохраняет работоспособность даже при экстремальных условиях внешней среды.

Из графика рис.2.5 видно, что при небольших значениях константы равновесия k и l= mсостояние гомеостаза не имеет достаточного запаса по устойчивости и при небольших изменениях lи mвероятности состоянийсущественно меняются. При больших значениях k эти же вероятности практически не меняются, т.е. состояние гомеостаза является более устойчивым. Для более тщательного изучения этой проблемы были получены уравнения для зависимости изменения вероятностей состояний амбивалентной системы от константы равновесия k и на рисунке 2.6 построены графики этой

зависимости

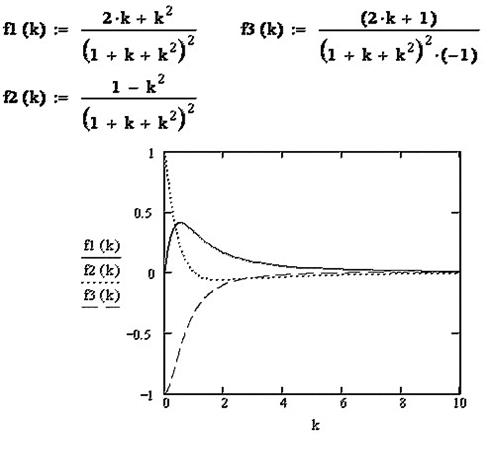
Рис.2.6

Действительно, как показывает рис.2.6, при малых значениях k (0 < k < 4) имеет место значительное изменение вероятностей состояний, а при больших значениях k (k > 6) изменение вероятностей состояний практически равно нулю. Таким образом, наглядно доказывается наличие двух разных гомеостазов в амбивалентных системах. Если ввести некоторый интервал изменения вероятностей состояний,внутрикоторого сохраняется гомеостаз, то, как видно из рис.2.6, при малых значениях k интервал изменения вероятностей, при котором сохраняется этот гомеостаз незначителен, а при больших значениях k такое изменение может быть очень большим.

2.1.1.Анализ устойчивости амбивалентных систем в установившемся режиме

Как было показано выше, амбивалентная система с тремя состояниями описывается следующей системой дифференциальных уравнений:

с нормировочным условием: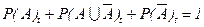

Представляет интерес исследование полученной системы на устойчивость. Так как то для исследования установившегося режима (гомеостаза) достаточно рассмотреть уравнения:

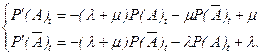
В точке равновесия 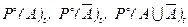, когда 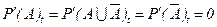, получаем систему алгебраических уравнений, решение которых дает следующие выражения для вероятностей существования двух противоположностей А, и их смеси A È :

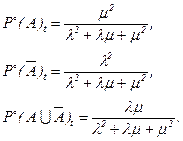
Задавая приращения и 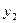в точке равновесия можно обозначить , параллельный перенос системы координат (рис.2.7) в точку равновесия дает следующую зависимость:

или, что тоже самое:

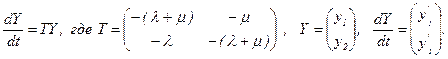
Осуществляя ортогональное преобразование (рис. 2.8) S, данную систему можно свести к диагональному виду: 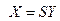и тогда система примет вид 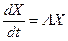, где L - диагональная матрица, у которой элементы - собственные значения матрицы Т.

Рис. 2.7 Рис. 2.8

Находим эти собственные значения n:

Система 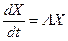принимает вид:

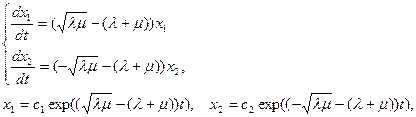
значит: .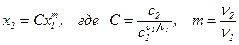

График этой зависимости представляет из себя семейство парабол, если m>0. Траектории образуют, так называемый, устойчивый узел:

Рис.2.9 Рис.2.10

Если m<0, то соотношение описывает семейство гипербол и точка равновесия является точкой типа “седло” (рис. 2.9).

Однако, так как l > 0, m > 0, тоn₂<0.

Рассмотрим n₁. Предположимn₁>0, значит

Получим: 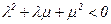, что невозможно. Итак, n₁<0, тогда m>0 и точка равновесия – устойчивый узел, т.е. такая система всегда стремится к устойчивому равновесию.