Применение теории Марковских цепей для анализа амбивалентных систем

Марковские процессы - другой интересный математический метод, который можно использовать для описания систем с группировками, предполагая, что в коллективе действует механизм случайности. Достоинство этого метода заключается в том, что можно проводить анализ поведения коллективов с большим числом участников, часть членов которых могут общаться между собой или не общаться между собой, причем характер общения может быть как односторонним, так и двухсторонним.

Основным понятием в теории Марковских процессов является понятие состояния, когда исследуемый объект или система (коллектив) с течением времени переходит из одного состояния в другое, например, от хаоса к порядку, от одной стратегии управления к другой и т.д. Для полного описания такой системы задают матрицу переходов и начальное распределение вероятностей состояний 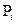, где i, j – номера состояний системы.

Наиболее простой моделью является простая однородная цепь Маркова, когда следующее состояние зависит только от состояния в предыдущий момент времени и вероятности переходов не зависят от времени.

Различают два основных типа Марковских цепей: эргодическая цепь и поглощающая. Для первой характерным признаком является достижимость любого состояния из любого другого; для второго типа – наличие состояний, попав в которые система в них остается навсегда.

Как было сказано выше, характерным признаком для амбивалентных систем является то, что в них действуют две противоположности, которые переходят друг в друга и в результате этого могут образовывать промежуточное состояние. В связи с этим в качестве математической модели предлагается Марковская цепь первого типа, т.е. эргодическая цепь. На рис. 2.34 показан граф амбивалентной системы, в которой действуют две противоположности А и В и их смесь А U В. Характерным для этого графа является то, что отсутствует переход системы за один шаг из состояния смеси в это же самое состояние, но как будет показано дальше уже через два шага система с некоторой вероятностью будет оставаться в этом состоянии.

P

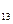
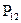
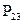
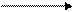
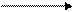
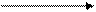
P P

P P

P P

P

Рис.2.34

Согласно теории Марковских цепей такие цепи называются регулярными цепями, обладающими неподвижным вектором строкой, показывающим распределение вероятностей состояний, в которых система

пребывает в установившемся режиме.

Матрица переходов для графа, приведенного на рисунке, выглядит следующим образом:

,

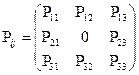Здесь - вероятность перехода амбивалентной системы из состояния i в состояние j за один шаг. Определим вероятность перехода системы через два шага.

.

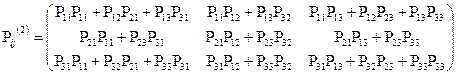Как видно из матрицы при положительных значениях вероятностей перехода все состояния данной системы достижимы из других состояний, т.е. в амбивалентной системе существует стационарный режим, на который вектор начального состояния не влияет.

Приведенные матрицы вполне могут описывать поведение не только бинарных систем с двумя противоположностями, но и, например, коллектива из трех членов - руководителей малого предприятия, между которыми существуют симпатии и антипатии, равнодушие или безразличие.

При определенных параметрах коллектива на такой модели можно показать будущее развитие системы, а именно, если процесс эргодический, то указать состояние равновесия. Более того, интерес представляют динамические характеристики, такие, например, как среднее время перехода системы из начального состояния в поглощающее, среднее время нахождения системы в выделенном состоянии и др.

Приведем основные результаты теории регулярных Марковских цепей, которые понадобятся для анализа конкретных практических примеров амбивалентных систем [17].

1.Если 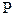- регулярная переходная матрица, то степени 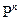(при n→∞) стремятся к вероятностной матрице A, называемой предельной матрицей, каждая строка которой представляет один и тот же вероятностный вектор 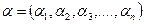, все компоненты которого положительны.

Так как предельный вектор 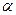зависит только от P, но не от начального распределения, то можно сказать, что долгосрочное прогнозирование о поведении регулярной цепи не зависит от начальных вероятностей.

Для нахождения вектора 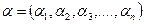необходимо отыскать вероятностное решение уравнения 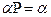, т.е. найти решение следующей системы уравнений:

1=

……………………………….

.

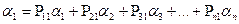
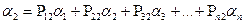
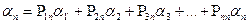Единственное решение этой системы и есть вектор .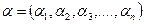

И, следовательно, сразу же находится и предельная матрица

.

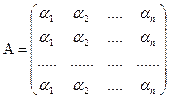Здесь следует отметить, что элементы предельной матрицы показывают долю времени проводимого системой в каждом из состояний.

2.Большое значение для вычисления ряда интересных характеристик имеет, так называемая фундаментальная матрица регулярной Марковской цепи.

Если P- регулярная переходная матрица, то матрица

Z = (I- (P – A))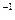

называется фундаментальной матрицей Марковской цепи, определяемой P. Хотя некоторые свойства фундаментальной матрицы и совпадают со свойствами переходной матрицы, например, 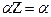, ее элементы не обязаны быть неотрицательными. В этом выражении матрица I – единичная матрица.

3. Для любой регулярной цепи Маркова и любого начального распределения π среднее время, проведенное в состоянии 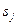за первые n шагов 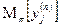отличается от n 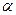на величину, равную πZ - 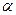. Отсюда получаем следствие, что для любых двух начальных распределени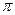й и 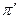, разница между средним временем, проведенном в состоянии 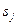равна ( 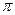- 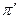)Z. Таким образом, элементы матрицы (Z – A) дают интересную численную характеристику регулярной цепи, зависящей от начального состояния. Таким образом, согласно этому следствию можно сравнить различные начальные положения, например, i и k:

- = .

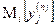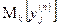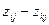4. Для регулярной цепи Маркова вводится понятие времени первого достижения 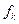, которое равно числу шагов, за которое цепь впервые попадает в из начального состояния и доказывается теорема, что при любом i математическое ожидание 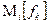конечно. Матрица M средних времен достижения дается формулой:

M = (I – Z + EZ 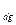)D,

где D – диагональная матрица с диагональными элементами = 1/ ,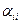

Z 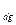- матрица, полученная из Z заменой всех элементов, не лежащих на главной диагонали, нулями.

5. Фундаментальная матрица Z позволяет найти и дисперсию моментов первого достижения 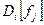, которая вычисляется как:

= - .

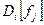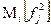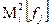Обозначим через W матрицу с элементами 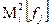, которая вычисляется по следующей формуле:

W = M (2Z 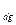D - I) + 2(ZM – E (ZM) ).

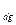Обозначим матрицу дисперсий через M 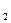, тогда M 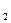= W - M 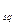, где M 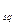- матрица, полученная из M возведением в квадрат каждого элемента.

6. Большой интерес для амбивалентных систем представляет использование, так называемой, матрицы обмена, которая характеризует процесс обмена между состояниями цепи Маркова в установившемся (стационарном) режиме, не зависящем от начального положения. Условие обратимости сводится к тому, чтобы матрица обратимости D 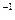P была симметрична, т.е. .

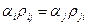Применяя теорию регулярных цепей Маркова и теорию матриц, можно решить ряд практических задач для анализа амбивалентных систем. Одна из таких задач заключается в том, чтобы найти то количество шагов, при котором регулярная переходная матрица P сходится к предельной матрице A.

Из теории матриц известно, что детерминант произведения матриц равен произведению детерминантов, т.е. для нашего случая

.

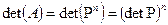Так как детерминант матрицы A равен нулю, а детерминант матрицы P всегда меньше единицы, то это равенство справедливо при значении 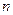, равному бесконечности. Для конечного значения 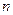произведение детерминантов не будет равно нулю и, следовательно, оно принимается равным некоторому достаточно малому значению 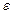не равному нулю. Это значение будет определять точность получения предельной матрицы.

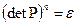
Решая полученное уравнение, относительно 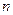находим, что

.

Здесь следует заметить, что разность между элементами финальной матрицы 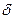будет всегда больше чем 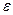. Поэтому рекомендуется принимать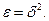

Очень часто требуется решить обратную задачу: для заданной точности и заданного количества шагов рассчитать значение детерминанта переходной матрицы P. Решая выше приведенное уравнение относительно детерминанта P, находим, что

,

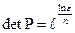где 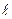- основание натуральных логарифмов.

Для заданной точности 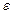= 0,001, по выведенной формуле, рассчитаем значение детерминанта для различного значения количества шагов n:

Рассчитанные значения детерминанта могут быть использованы для расчета элементов переходной матрицы.

2.4.Методы оценки степени остроты противоречия в амбивалентных системах

Как было показано выше, в амбивалентных системах возникает состояние гомеостаза (как постоянство внутренней среды организма), при котором существует внутреннее противоречие между противоположностями, которое собственно и обеспечивает сохранение этого постоянства.

Возникает проблема оценки степени остроты этого противоречия, тем более, что при определенных соотношениях между интенсивностями противоположностей, наблюдаются, по крайней мере, два состояния гомеостаза, которые автор называет «мягким» и «жестким» и, естественно, что в этих состояниях уровень противоречий разный.

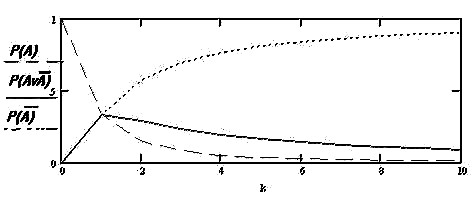
Как видно из приведенного рисунка при 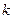=1 наблюдается состояние «мягкого» гомеостаза, при котором уровни двух противоположностей и их смеси 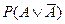одинаковы. Можно высказать предположение, что в этом состоянии острота противоречия не велика.

При kзначительно больше или меньше единицы наблюдается состояние «жесткого» гомеостаза, при котором одна из противоположностей преобладает над другой и, очевидно, что в этом состоянии острота противоречия значительно больше.

Для количественной оценки остроты противоречия можно предложить два варианта кусочно-линейный и нелинейный: первый вариант связан с линейной зависимостью от параметра 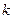на разных интервалах его изменения от нуля до единицы и от единицы до бесконечности или, по крайней мере, до некоторой большой величины, например, до 10. Зависимость остроты противоречия (обозначим ее символом Q) от этого параметра в целом будет иметь нелинейный характер. Действительно, при kизменяющимся от 0 до 1 острота противоречия будет падать от максимального значения до минимального, а при kизменяющегося от 1 до 10 увеличиваться от минимального до максимального. Выберем в качестве минимального значения остроты противоречия значение равное нулю, а в качестве максимального значения значение равное 100%. Здесь следует уточнить, что оценивается не само противоречие, а именно, острота противоречия, т.е. противоречие имеет место быть, но его острота может равняться, например, нулю. С учетом этого предложения функциональная зависимость Q(k) будет иметь следующий вид:

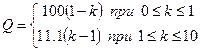
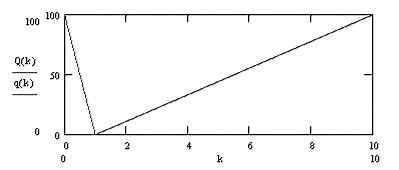
рис.2.35

На рис.2.35 показан график зависимости остроты противоречия от соотношения между противоположностями, из которого видно, что если в системе одна из противоположностей преобладает, то острота противоречий возрастает и только при равенстве интенсивностей противоположностей (k=1) она равна нулю.

Второй вариант количественной оценки остроты противоречия связан с тем обстоятельством, что в амбивалентных системах, в процессе их функционирования, возникает третье состояние, которое автор называет смесью двух противоположностей. Например, в системе «любовь - ненависть» появляется дружба, в системе «белый - черный» появляются метисы, в системе «симпатия - антипатия» возникает безразличие и т.д. Количественная оценка уровня этого состояния смеси 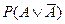в зависимости от параметра kимеет следующий вид:

.

На рис.2.4 эта зависимость показана сплошной линией. Можно высказать предположение, что наличие смеси в системе это, как - бы, результат того, что острота противоречия минимальна. Смешанные браки между разными народами могут быть только на основе дружбы, наличие безразличия между членами коллектива не вызывает каких - либо конфликтов, то - есть, чем выше уровень смеси, тем меньше острота противоречия и, наоборот, чем меньше уровень смеси, тем выше острота противоречия.

Если, также как в первом варианте принять условие, что при k=1 острота противоречия равна нулю, то зависимость ее от параметра k, выраженная в процентах, имеет следующий вид

.

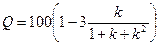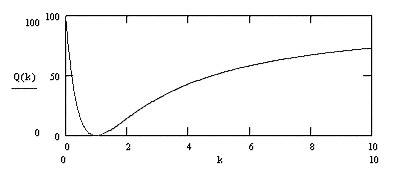
рис.2.36

На рис.2.36 показан график этой зависимости, из которого видно, что с увеличением параметра kв отличие от первого варианта нет резкого возрастания остроты противоречия до 100 процентов. Это объясняется тем, что при больших значениях k, какой то отличный от нуля уровень смеси остается и, следовательно, напряженность между противоположностями ослабляется. При втором варианте можно непосредственно измерять остроту противоречия через вероятность наличия смеси по формуле:

Q= 100-300 P(AÚĀ),

где P(AÚĀ)изменяетсяот 0 до 1/3.

Практическое применение предлагаемых в статье формул, в частности по первому варианту, для оценки остроты противоречия может вызвать определенные трудности, так как измерять интенсивности переходов между противоположностями (λ и µ) можно только в технических системах, например, в химических системах с прямой и обратной реакцией, как правило, скорости этих реакций известны. Для социальных систем таких возможностей нет, автор, к сожалению, не может рекомендовать способ измерения интенсивности перехода от любви к ненависти и обратно, от антипатии к симпатии и обратно и т.д.

Второй вариант оценки остроты противоречия кажется более предпочтительным, так как измерять уровень смеси в амбивалентных системах, как в технических, так и в социальных можно по статистическим данным.

Так, например, оценивать напряженность в смешанных браках можно по количеству браков и разводов между черными и белыми, украинцами и русскими, грузинами и армянами и т.д. Степень социальной напряженности в обществе можно измерять по величине среднего класса, степень остроты противоречия в семейных отношениях измерять по количеству заключаемых браков и разводов между молодыми людьми и т.д.

Предложенные формулы для оценки противоречия позволяют поставить обратную задачу вычисления параметра kпри заданном значении Q. Здесь можно привести следующие рассуждения: если требуется, чтобы острота противоречия была равна нулю, то необходимо иметь значение kравным единице, но в этом случае, как было показано выше, имеет место «мягкий» гомеостаз, в котором система работает не эффективно и для увеличения эффективности необходимо смещать точку равновесия. Этот вывод был сделан для химической реакции, но он, очевидно, может быть обобщен и на другие системы на основании применения принципа Ле-Шателье.

При Q 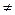0, задаваясь конкретным численным значением Q, по предложенным формулам вычисляем либо параметр k, либо уровень смеси, соответствующий данной оценке противоречия. Например, для Q= 50% по линейной формуле получаем k= 0,5 или k= 5,5, для второго варианта по нелинейной зависимости уровень смеси P(AÚĀ)= 0,17.

В качестве подтверждения того, что обратная задача нахождения соответствующего компромисса между противоположностями реальна, приведем результаты исследований британских ученых, которые разработали математическую модель настоящей и вечной любви. По их утверждению, эти расчеты позволяют установить, долго ли продлятся отношения пары с точностью до 94%. Участникам исследований предлагалось в течении 15 минут поговорить на темы, по которым пары имеют противоположные мнения: деньги, секс, политика, отношения с родителями и т.д. После беседы составлялся график пересечения ответов жены и мужа. Чем чаще пересекались линии, тем больше шансов на успех было у этого брака, иные результаты свидетельствовали о скором разводе. Очевидно, что неплохо было бы эту формулу применять ещё до вступления в брак, тогда количество разводов было бы значительно меньше.