Основы теории крыла
Гребные винты, рули, и другие судовые устройства имеют общий принцип действия, рассматриваемый в теории крыла. Для изучения работы этих устройств необходимо иметь представление о силах, действующих на крыло при движении.
Геометрические характеристики крыла определяются (рис.5.):
- площадью крыла F и формой проекции крыла в плане;
- длиной (размахом) крыла l - размером крыла в направлении,
перпендикулярном набегающему потоку;
- профилем крыла - сечением крыла плоскостью, перпендикулярной его размаху;
- хордой крыла b (шириной крыла) – отрезком прямой, соединяющей крайние точки профиля; при переменной по размаху крыла хорде вводится понятие средней хорды:
bср = F / l;
- максимальной толщиной профиля t – расстоянием между крайними точками профиля перпендикулярно хорде.
Часто пользуются безразмерными геометрическими характеристиками крыла:
- удлинением (относительным размахом) крыла λ = l /bср = l2 /F или (для прямоугольного крыла) λ = l / b;
- относительной толщиной 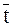 = 100 t / b - отношением наибольшей толщины профиля к длине хорды.
= 100 t / b - отношением наибольшей толщины профиля к длине хорды.
Nbsp; Рис.5. Геометрические характеристики крыла
Гидродинамические характеристики крыла (рис.6.) определяются его геометрией и углом α между хордой профиля крыла и направлением скорости движения его, называемым углом атаки. Поток, набегающий на крыло со скоростью υ под углом атаки α, на верхней поверхности крыла ускоряется, а на нижней - замедляется. Согласно уравнению Бернулли, на нижней поверхности создается повышенное давление, а на верхней - пониженное. Кроме сил давления, на движущееся в вязкой жидкости крыло действуют касательные силы трения. Силы гидродинамического давления и касательные силы трения приводятся к главному вектору гидродинамических сил Р.
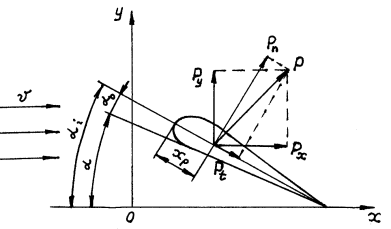
Рис.6. Схема действия потока жидкости на крыло
Спроектировав главный вектор на направление движения и перпендикулярное ему направление, получим силу профильного Рx и подъемную силу крыла Ру:
Рx = Р cos(Р, x); Ру= Р cos(Р, y).
Также можно определить составляющие силы Р направленных по нормали и по касательной к крылу. Нормальная составляющая силы Р:
Рn = Рy cos α + Рх sin α;
Тангенциальная составляющая силы Р:
Рt = Рx cos α - Рy sin α;
Точка приложения силы Р называется центром давления. Центр давления отстоит от передней кромки крыла на расстоянии хр. Момент относительно передней кромки крыла М = Рn хр.
Отношение подъемной силы крыла к его сопротивлению называется коэффициентом гидродинамического качества крыла
К = Рy / Рх = С y / Сх.
Коэффициент обратного качества ε = Рх/ Рy.
В соответствии с общей формулой для гидродинамических сил определяется силы и моменты, действующих на крыло при движении:
Рy = 0,5 С y ρ υ2 F; Рx = 0,5 С x ρ υ2 F;
Рn = 0,5 С n ρ υ2 F; Рt = 0,5 С t ρ υ2 F;
M = 0,5 С m ρ υ2 F b,
где Сy , Сx , Сn , Сt , Сm - безразмерные коэффициенты подъемной силы, сопротивления, нормальной силы, касательной силы и момента. Отношение абсциссы центра давления крыла к длине хорды хр / b = С р, называется коэффициентом центра давления крыла, тогда
С m = С n С р.
Безразмерные коэффициенты определяют гидродинамические характеристики крыла. Обычно задают независимые коэффициенты: Сy, Сx , Сm (Ср), так как остальные коэффициенты являются зависимыми.
Для данного крыла коэффициенты Сy ,Сx , Сn ,Сt , Ср ,Сm , К(ε) зависят от угла атаки α, чисел Рейнольдса Re, Фруда Fr, а также от условий движения крыла (в безграничной жидкости, вблизи свободной поверхности жидкости, кавитации и т.п.). Они определяются теоретическим или чаще экспериментальным путем, поэтому для геометрически подобных крыльев они задаются в функции от угла атаки при установившемся обтекании потоком жидкости с некоторым числом Re. Значения гидродинамических коэффициентов крыла, в общем случае завися от числа Re, однако, при обтекании крыла без кавитации безграничным потоком несжимаемой жидкости с числом Re > (1,31,5) 106 коэффициенты оказываются в автомодельной области и их можно считать независимыми от Re.
На рис.7. приведены кривые зависимости гидродинамических характеристик крыла от углов атаки. Из рисунка видно, что коэффициент подъемной силы с увеличением угла атаки вначале возрастает, а затем, достигнув максимума при так называемом критическом угле атаки αкр, начинает резко падать. Для симметричного профиля подъемная сила становится равной нулю при нулевом угле атаки, для несимметричного -при значениях α, отличных от нуля. Угол атаки, при котором Сy обращается в нуль, называют углом нулевой подъемной силы α0, а угол αi = α + α0 - гидродинамическим углом атаки. Направление потока, соответствующее углу α0, называется направлением нулевой подъемной силы.
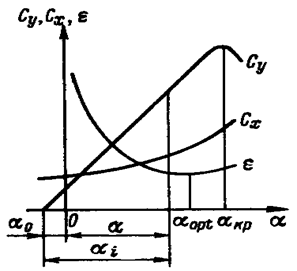
Рис.7. Кривые зависимости гидроди-намических характеристик крыла от углов атаки
Из рис.7. следует, что существует такое значение угла атаки, при котором коэффициент обратного качества минимальный. Этот угол называют наивыгоднейшим углом атаки αорt.
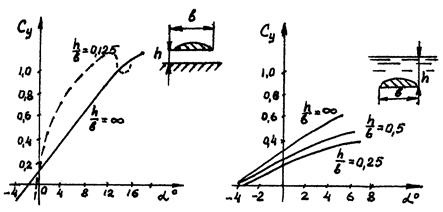 |
На гидродинамические характеристики крыла сильно влияют границы потока (рис.8). Влияние твердой стенки под крылом приводит к увеличению коэффициента его подъемной силы, а по мере уменьшения погружения крыла к заметному снижению величины С y.
Рис.8. Графики влияния твердой стенки и свободной поверхности жидкости на С y прямоугольных крыльев.
Дата добавления: 2014-12-09; просмотров: 2133;
