Вектор электрического смещения. Граница двух диэлектриков
Источником электростатического поля являются свободные и связанные электрические заряды: линии напряженности начинаются на положительных зарядах (или в бесконечности) и оканчиваются на отрицательных (или в бесконечности).
Однако при решении задач, связанных с электрическим полем в диэлектрике, в ряде случае оказывается более удобным учитывать только поле свободных зарядов. Для этого вводится понятие вектора электрического смещения ( 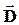 ).
).
Рассмотрим изменение электрического поля на достаточно протяженной границе двух однородных и однородно поляризованных диэлектриков 1 и 2.
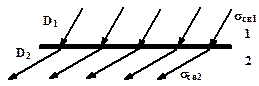
| В первом диэлектрике напряженность электрического поля и вектор поляризации соответственно равны 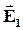 и и 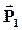 , во втором диэлектрике - , во втором диэлектрике - 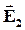 и и 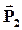 . .
|
В общем случае все эти четыре вектора произвольно ориентированы в диэлектриках, поэтому можно говорить об их тангенциальных к границе раздела (Et1, Et2 и Pt1, Pt2) и нормальных (En1, En2 и Pn1, Pn2) составляющих.
На границе возникнут связанные электрические заряды противоположных знаков, поверхностные плотности которых равны sсв1 и sсв2. Эти заряды создадут электрическое полеE’. Напряженность E’ уменьшит нормальную составляющую напряженности в одном диэлектрике и увеличит в другом, поэтому E’будет определятьсяразностью нормальных составляющих напряженности:
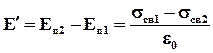
Это уравнение можно записать так:
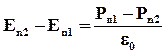
или:
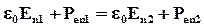
Отсюда видно, что на границе двух диэлектриков сохраняется нормальная составляющая:
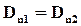
некоторого вектора:
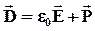
Это и есть вектор электрического смещения.
Т.е. можно говорить о линиях электрического смещения и о потоке вектора электрического смещения через некоторую поверхность.
Поток вектора электрического смещения не изменятся на границе двух диэлектриков, т.е. линии этого вектора не начинаются и не заканчиваются на связанных зарядах, а линии напряженности поля начинаются и заканчиваются на связанных зарядах.
Из приведенных соотношений видно,
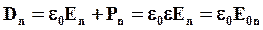
Внутри диэлектрика 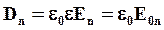 , в вакууме
, в вакууме 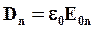 .
.
Видно, что величина Dn остается постоянной при переходе из вакуума в среду, а величина En изменяется.
Или в векторной форме:
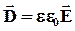
Запишем для нашего случая теорему Гаусса. Общий заряд в диэлектрике qобщ можно найти как разность свободных зарядов и связанных зарядов.
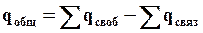
Сумма 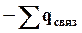 взята со знаком минус потому, что поле связанных зарядов направлено противоположно полю свободных зарядов.
взята со знаком минус потому, что поле связанных зарядов направлено противоположно полю свободных зарядов.
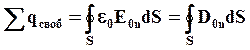
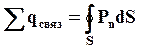
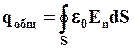
Получаем:
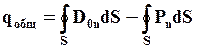 – теорема Гаусса для поля внутри диэлектрика: поток вектора электрического смещения сквозь замкнутую поверхность равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности:
– теорема Гаусса для поля внутри диэлектрика: поток вектора электрического смещения сквозь замкнутую поверхность равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности:
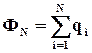
Запишем в виде:
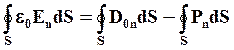
отсюда получаем: 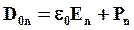
Величина поля внутри диэлектрика:
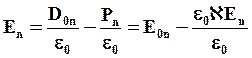 Þ
Þ 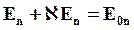
или:
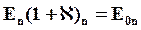 Þ
Þ 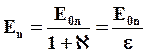
В других конкретных случаях соотношения для электростатического поля с диэлектриком имеют другой вид и чаще всего значительно более сложный, нежели полученные нами для плоской пластины внутри конденсатора. В частности, в некоторых случаях введение диэлектрика сопровождается не только ослаблением поля, но и его усилением.

| Поле, созданное зарядом q в т. A и B, по направлению совпадает с полем связанных зарядов диэлектрика M, внесенного в поле заряда q. |
В т. C величины E0 и E’ направлены в противоположные стороны, т.е. в этой точке внесение диэлектрика сопровождается ослаблением поля.
Напряженность электрического поля точечного заряда q в диэлектрике выражается формулой:
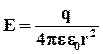
Получаем выражение для электрического смещения поля точечного заряда:
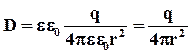
Как видно, электрическое смещение в однородном изотропном диэлектрике не зависит от свойств вещества.
Дата добавления: 2014-12-09; просмотров: 3715;
