Розрахунок міцності перерізів на першу комбінацію
Розміри поперечного перерізу: 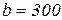 мм,
мм, 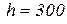 мм, відстань від нижньої грані перерізу до осі розтягнутої арматури
мм, відстань від нижньої грані перерізу до осі розтягнутої арматури 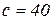 мм, робоча висота перерізу
мм, робоча висота перерізу 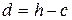
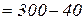
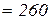 мм, відстань від верхньої грані перерізу до осі розтягнутої арматури
мм, відстань від верхньої грані перерізу до осі розтягнутої арматури 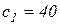 мм; розрахункова висота
мм; розрахункова висота 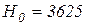 мм.
мм.
Бетон важкий класу С16/20; розрахункова міцність на стиск 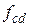 = 11,5МПа, значення відносних деформацій
= 11,5МПа, значення відносних деформацій 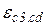 = 0,580/00 = 0,00058 і
= 0,580/00 = 0,00058 і 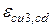 = 3,230/00 = 0,00323, модуль пружності Еcd = 20 ГПа =20000 МПа (табл. Б.3).
= 3,230/00 = 0,00323, модуль пружності Еcd = 20 ГПа =20000 МПа (табл. Б.3).
Робоча арматура стінки резервуару, монолітної плити покриття та колон може бути класу А400С, з характеристичним значення опору арматури на межі текучості 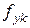 = 400 МПа, з коефіцієнтом надійності для арматури, який приймається згідно з таблицею Б.4, γs = 1.1, розрахункове значення опору арматури на розтяг fyd = fyk / γs = 400/1.1=363.64 МПа, , модуль пружності
= 400 МПа, з коефіцієнтом надійності для арматури, який приймається згідно з таблицею Б.4, γs = 1.1, розрахункове значення опору арматури на розтяг fyd = fyk / γs = 400/1.1=363.64 МПа, , модуль пружності 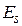 = 210000 МПа, величина відносних деформацій
= 210000 МПа, величина відносних деформацій 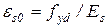 = 363.6363/210000 = 0,001732 = 1,732 ‰ та
= 363.6363/210000 = 0,001732 = 1,732 ‰ та 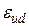 = 0,025 = 25‰ (див. табл. Б.4).
= 0,025 = 25‰ (див. табл. Б.4).
Розрахунковий згинаючий момент в перерізі від зовнішнього навантаження 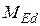 =
= 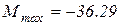 кН.м; розрахункова поздовжня сила в перерізі від зовнішнього навантаження
кН.м; розрахункова поздовжня сила в перерізі від зовнішнього навантаження 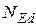 =
= 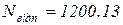 кН.
кН.
Розрахункова довжина колони дорівнює (рис. 5.1,д):
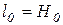
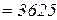 мм.
мм.
Розраховуємо випадковий ексцентриситет 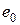 ,який слід приймати не меншим за:
,який слід приймати не меншим за:
- 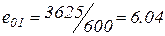 мм;
мм;
- 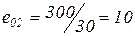 мм;
мм;
- 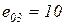 мм.
мм.
Остаточно приймаємо більше з трьох значень 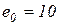 мм.
мм.
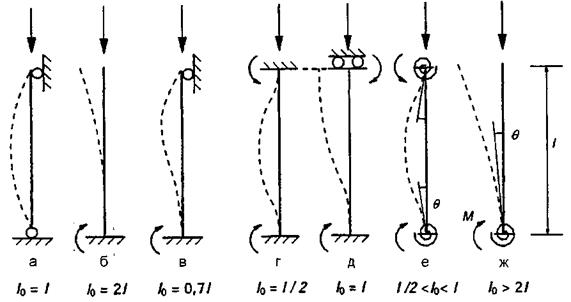
Рисунок 5.1 – Приклади різних форм втрати стійкості та відповідних розрахункових довжин окремих елементів
Для елементів статично невизначених конструкцій значення ексцентриситету поздовжнього зусилля відносно центру ваги приведеного перерізу e приймають таким, що дорівнює величині ексцентриситету 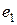 , отриманого зі статичного розрахунку, або випадкового ексцентриситету
, отриманого зі статичного розрахунку, або випадкового ексцентриситету 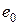 (більша з цих величин):
(більша з цих величин):
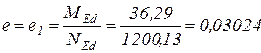 м = 30,24 мм
м = 30,24 мм 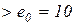 мм.
мм.
1. Перевіряємо необхідність урахування поздовжнього вигину.
Мінімальна гнучкість колони
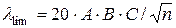
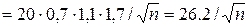
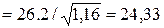 ,
,
де може використовуватися А = 0,7; В = 1,1; С = 1,7; 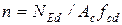
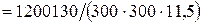
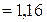 - відносна осьова сила (
- відносна осьова сила ( 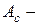 площа бетону поперечного перерізу колони).
площа бетону поперечного перерізу колони).
Фактична гнучкість колони
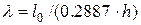
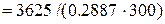
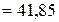 .
.
Так як 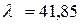 >
> 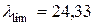 – необхідно врахувати гнучкість колони.
– необхідно врахувати гнучкість колони.
Згідно з методом номінальної кривизни, додатковий максимальний прогин (ексцентриситет) 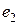 , викликаний подовжнім вигином, визначаємо по спрощеній залежності
, викликаний подовжнім вигином, визначаємо по спрощеній залежності
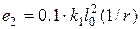
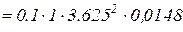
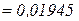 м
м 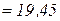 мм,
мм,
де 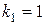 при
при 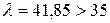 ;
;
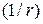 - кривизна стиснутого елементу в розрахунковому перерізі, яку допускається визначати по формулі
- кривизна стиснутого елементу в розрахунковому перерізі, яку допускається визначати по формулі
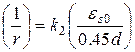
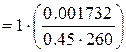
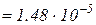 мм-1 =
мм-1 = 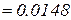 м-1,
м-1,
де 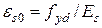
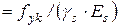
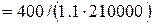
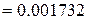
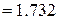 ‰ - відносна деформація арматури на межі текучості; k2 = 1, що забезпечить більшу надійність конструкції.
‰ - відносна деформація арматури на межі текучості; k2 = 1, що забезпечить більшу надійність конструкції.
Сумарний розрахунковий ексцентриситет відносно центру ваги приведеного перерізу за формулою
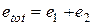
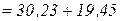
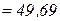 мм.
мм.
2. Знаходимо згинаючий момент відносно осі розтягнутої арматури
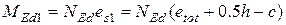
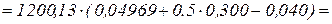
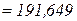 кН.м,
кН.м,
де 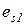 - відстань від лінії дії сили
- відстань від лінії дії сили 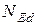 до осі розтягнутої (менш стиснутої) арматури
до осі розтягнутої (менш стиснутої) арматури 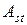 (рис. 5.2).
(рис. 5.2).

Рисунок 5.2 - Напруження і деформації в перерізі при позацентровому стиску
3. Визначаємо необхідні для розрахунку коефіцієнти:
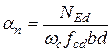
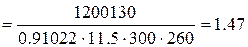 .
.
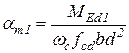
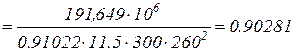 ;
; 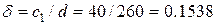 ;
;
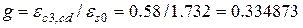 ;
; 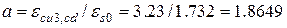 .
.
Коефіцієнт прямокутної частини білінійної епюри напружень 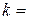
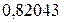 та коефіцієнт центра ваги епюри напружень
та коефіцієнт центра ваги епюри напружень 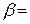
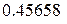 , коефіцієнт повноти білінійної епюри напружень
, коефіцієнт повноти білінійної епюри напружень 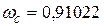 (для бетону класу С16/20) приймаємо згідно таблиці Б.5. Для армування плити приймаємо арматуру класу А400С.
(для бетону класу С16/20) приймаємо згідно таблиці Б.5. Для армування плити приймаємо арматуру класу А400С.
4. Приймаємо 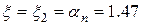 .
.
Оскільки
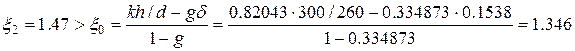 ,
,
то знаходимо
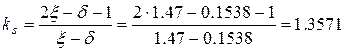 .
.
Уточнюємо значення 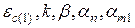 при
при 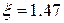 .
.
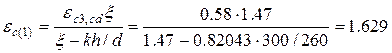 ‰.
‰.
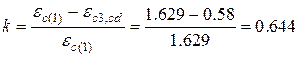 ;
; 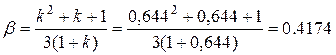 .
.
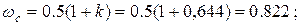
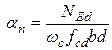
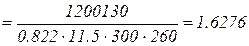 .
.
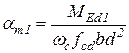
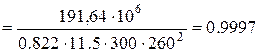 .
.
Тоді
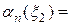
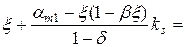
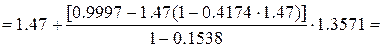 2.162
2.162 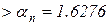 .
.
Оскільки 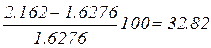 %
% 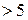 %, то продовжуємо ітерації.
%, то продовжуємо ітерації.
5. Приймаємо 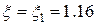 . Оскільки
. Оскільки 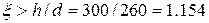 то переріз деформується в області 4 і знаходимо
то переріз деформується в області 4 і знаходимо 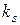 по формулі (27) :
по формулі (27) :
Оскільки
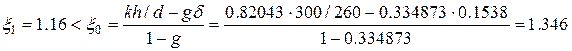 ,
,
то 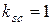 і
і
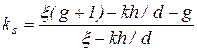 =
=
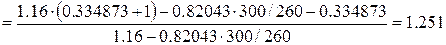 .
.
Уточнюємо значення 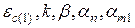 при
при 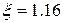 .
.
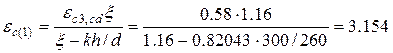 ‰.
‰.
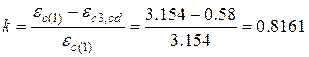 ;
; 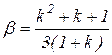
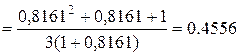 .
.
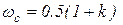
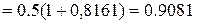 ;
;
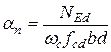
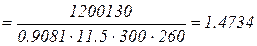 .
.
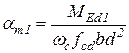
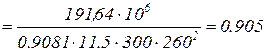 .
.
Тоді
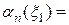
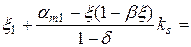
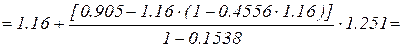 1.6893
1.6893 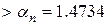 .
.
Оскільки 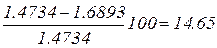 %
% 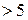 %, то продовжуємо ітерації.
%, то продовжуємо ітерації.
У зв’язку з тим, що 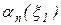
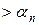 та
та 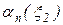
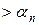 . Рішення потрібно шукати в області 3.
. Рішення потрібно шукати в області 3.
6. Приймаємо 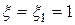 .025. Оскільки
.025. Оскільки 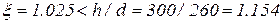 , то переріз деформується в області 3.
, то переріз деформується в області 3.
Коефіцієнт прямокутної частини білінійної епюри напружень 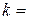
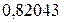 та коефіцієнт центра ваги епюри напружень
та коефіцієнт центра ваги епюри напружень 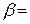
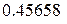 , коефіцієнт повноти білінійної епюри напружень
, коефіцієнт повноти білінійної епюри напружень 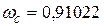 (для бетону класу С16/20).
(для бетону класу С16/20).
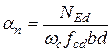
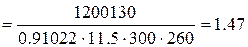 .
.
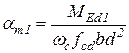
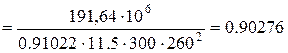 .
.
Знаходимо коефіцієнт
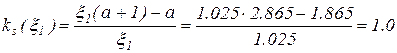 ,
,
де 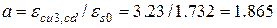
і визначаємо
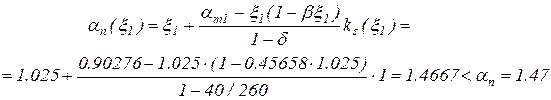
Оскільки
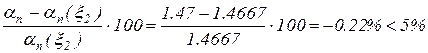
то припиняємо ітерації і можемо прийняти 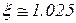
7. Потрібна площа симетричної арматури буде:
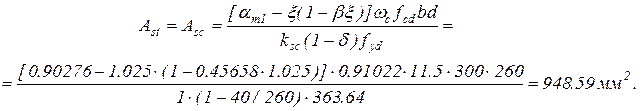
За конструктивними вимогами кількість поздовжньої арматури повинна бути не менше ніж 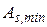 :
:
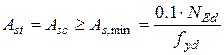 або
або 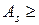
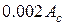 (більша із величин).
(більша із величин).

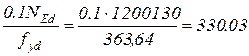 мм2 ;
мм2 ; 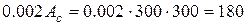 мм2
мм2
і не більше 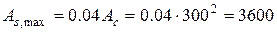 мм2, тому остаточно приймаємо потрібне розрахункове армування
мм2, тому остаточно приймаємо потрібне розрахункове армування 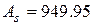 мм2.
мм2.
Вибираємо із сортаменту 2 Ø 25 А400С з 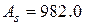 мм2
мм2 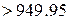 мм2.
мм2.
Дата добавления: 2014-12-09; просмотров: 1594;
