Методические указания к решению задач К 2.5, К 2.6
В задачах К 2.5 и К 2.6 требуется для сложных сечений вычислить значения главных центральных и моментов инерции и определить положение главных центральных осей.
Алгоритм решения этих задач.
1. Вычерчивают сложное сечение.
2. Сложное сечение разделяют на простые составляющие части.
3. Выбирают начальные оси Х0У0.
4. Определяют координаты центров тяжести составляющих частей в системе координат Х0У0. Через их центры тяжести проводят центральные оси составляющих частей, параллельные осям Х0У0. Вычисляют площади простых частей и их моменты инерции относительно проведенных центральных осей.
5. Определяют площадь и координаты центра тяжести всего сечения в системе координат Х0У0. Через центр тяжести сечения проводят центральные оси ХсУс параллельные осям Х0У0. Определяют моменты инерции сечения относительно этих осей.
6. Определяют главные центральные моменты инерции и положение главных центральных осей сечения.
Рассмотрим эти шаги более подробно.*)
Вычерчивание сечения
Сечение вычерчивается в произвольном масштабе на бумаге в клеточку или миллиметровке. Чертеж должен занимать не менее половины листа ученической тетради. На чертеже проставляют все характерные размеры сечения.
Деление сечения на простые части
Простой будет называть часть сечения, для которой известны положение центра тяжести, а также формулы для определения площади и центральных моментов инерции или их числовые значения. Для уменьшения числа составляющих частей, особенно для сечений с вырезами и отверстиями, допускается добавлять к сечению мнимые (отсутствующие) части. В расчетах площади и моменты инерции "мнимых" частей берутся с противоположным знаком по сравнению со знаком аналогичных действительных частей. Простые части нумеруют.
Выбор начальных осей
Решение можно выполнить с любыми, произвольно взятыми осями Х0У0, Однако затрат труда будет меньше, если начальные оси естественным образом связать с сечением. Для сечений несимметричных желательно начальные оси направлять по границам сечения или простых частей. Желательно, чтобы все сечение находилось в первой четверти. С целью устранения возможных ошибок следует выбирать только правую систему координат (ось У0 направлена вверх, ось Х0 – вправо). Для сечений симметричных желательно, чтобы начальные оси совпадали с осями симметрии.
__________________________________________________________
*)Примеры практического использования алгоритма даны в разд. 4.4
4-й шаг алгоритма
При выполнении этого и пятого шага алгоритма, для снижения вероятности появления ошибок, повышения удобства проведения расчетов, контроля и проверки их правильности, результаты расчетов заносят в единую таблицу (табл. 20). Порядок заполнения таблицы показан в разд. 4.3.
Таблица 20
| Часть | хс, | ус | F | Ix | Iv | Ixy | a | b | a2F | b2F | abF |
| … | |||||||||||
| N | |||||||||||
| Сечение |
Координаты центров тяжести определяют в системе координат Х0У0 с учетом знаков. Для этого используют размеры на чертеже и зависимости, определяющие координаты центров тяжести простых частей. Через центры тяжести простых частей проводят их центральные оси, параллельные осям Х0У0. По известным формулам определяют площади и моменты инерции простых частей относительно проведенных центральных осей. Если формулы для определения моментов инерции даны для центральных осей не параллельных осям Х0У0, то после определения моментов инерции относительно этих осей, определяют моменты инерции относительно центральных осей параллельных осям Х0У0, используя формулы для определения моментов инерции при повороте осей.
5-й шаг алгоритма
Определяют площадь сечения F
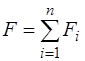 ,
,
где n – число простых частей; Fi – площадь i-ой части.
Координаты центра тяжести сечения определяют по формулам
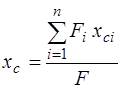 ;
; 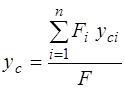 .
.
Здесь xci , уci – координаты центра тяжести i-ой части в системе координат Х0У0.
В сечениях, имеющих ось симметрии, центр тяжести находится на этой оси, в сечениях, имеющих две и более осей симметрии, - на пересечении осей симметрии.
Отмечают на чертеже центр тяжести и проводят через него центральные оси (Хс , Ус) сечения, параллельные осям Х0 , У0 . Вычисляют моменты инерции сечения относительно проведенных центральных осей по формулам
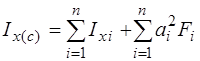 ;
;
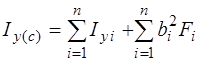 ; (*)
; (*)
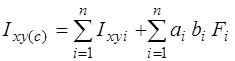 .
.
Здесь: аi= усi – ус – расстояние между центральной осью хi i-ой части и центральной осью Хc сечения; аi= усi – ус – расстояние между центральной осью уi i-ой части и центральной осью Уc сечения.
Расстояния аi , bi определяются с учетом знака.
Вычисляются 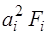 ,
, 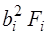 ,
, 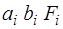 для каждой части и заносятся в табл. 15. Затем находят
для каждой части и заносятся в табл. 15. Затем находят 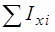 ,
, 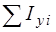 ,
, 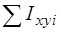 ,
, 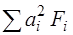 ,
, 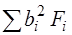 ,
, 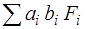 путем суммирования данных, записанных в соответствующих столбцах табл. 15. Далее находят Ix(c), Iу(c), Ixу(c), по формулам (*).
путем суммирования данных, записанных в соответствующих столбцах табл. 15. Далее находят Ix(c), Iу(c), Ixу(c), по формулам (*).
6-й шаг алгоритма
Определяют главные центральные моменты инерции сечения по формулам
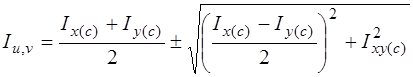 .
.
При определении Iu перед корнем берут знак плюс, при определении Iv - знак минус.
Определяют угол a между осью Хс и главной центральной осью u (осью, относительно которой осевой момент инерции максимальный)
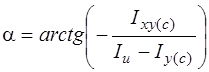 .
.
На чертеже сечения проводят главные центральные оси. Под углом a к оси Хс через центр тяжести сечения проводят ось u . Ось v проводят через центр тяжести перпендикулярно оси u.
Дата добавления: 2014-12-09; просмотров: 1104;
