Решение задач жёсткости

Здесь рассматривается решение задач жесткости при растяжении-сжатии и кручении. Решение задач жесткости при изгибе и сложных ви­дах нагружения бу­дет рассмотрено во второй части курса.

Условие жесткости формулируется так – перемещение в заданной точке или сечении конструкции не должно превышать допустимых, по условиям эксплуатации, пере­мещений этой точки или сечения.

Математические выражения условий жесткости:

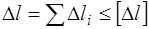- при растяжении-сжатии;

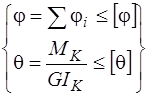- при кручении.

Здесь 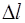– расчетное изменение длины расчетной схемы или её части; 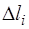– расчетные изменения длины входящих в них участков; 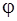– расчетный угол закручивания расчетной схемы или её час­ти; 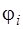– расчетные углы закручивания входящих в них участков; 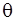– отно­сительный угол закручивания; 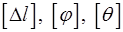– допускаемые: изменение длины, угол закру­чивания и относитель­ный угол закручивания.

В инженерной практике чаще всего решаются три типа задач жест­кости:

- проверка жесткости;

- определение размеров сечения, обеспечивающих за­данную жест­кость;

- определение допускаемой нагрузки, при которой обеспечивается жесткость конструкции.

Алгоритм решения этих задач включает в себя следующие шаги:

1. Выбор и изображение расчетной схемы;

2. Построение эпюр внутренних силовых факторов;

3. Запись условия жесткости;

4. Определение в численном или алгебраическом виде 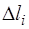, , 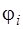вычис­ление , , .

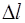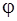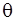Рассмотрим содержание этих шагов.

Выбор и изображение расчётной схемы и построение эпюр вы­полня­ются аналогично соответствующим шагам в алгоритме реше­ния задач прочности.

Запись условия жёсткости – содержание этого шага раскрыто выше.

Определение , ,. , , .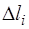

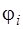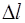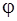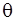На участках, где N = const, М_к = const:

, .

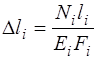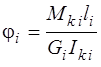На участках, где N ≠ const, М_к ≠ const:

, ,

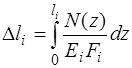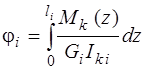где N(z), M_к(z) - аналитические выражения для определения N и М_к в произвольном сечении участка.

Эти выражения были составлены при построении эпюр.

Суммируя ∆l_i, получают выражение для ∆l, суммируя ∆ , полу­чают выражение для . Если условие жёсткости при кручении выра­же­но через 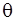, то записывают выражение для 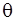(см. выше). Если рас­чет­ная схема состоит из стержней одного поперечного сечения, то в ка­честве М_к в выражение для 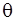подставляют максимальное по абсо­лют­ной величине значение ,взятое с эпюры ²М_к².

Если в расчетной схеме есть участки с разными поперечными се­че­ниями, то выражение для 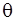составляют аналогично для каждого уча­стка.

Ответ на вопрос задачи

При проверке жесткости вычисляют численное значение ∆l , 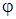, 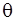и сравнивают с [∆l] , [ 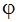] , [ ]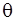. Если ∆l ≤ [∆l] , 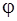≤ [ 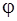] , 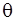≤ [ 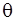] , то тре­буемая же­сткость обеспечена, иначе не обеспечена.

При определении необходимых размеров или допускаемой на­грузки в условие жесткости вместо знака "≤" ставят знак "=".

Для определения размеров в полученное равенство подставляют F, или I_k, выраженные через размеры сечения, затем разрешают его от­носительно размеров сечения.

При определении допускаемой нагрузки в равенство подстав­ляют N или М_к, вы­раженные через внешнюю нагрузку (если они не были уже выражены на этапе получения ∆l , 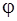, 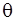), а затем разре­шают ра­венство относительно внешней на­грузки.

Предупреждение. Если задачи по определению размеров сечения или до­пускаемой нагрузки из условия жесткости решаются как самосто­ятельные, то после их решения в обязательном порядке необходима проверка прочности.