Решение задач прочности

Чаще всего условие прочности формулируется в следующем виде - макси­мальные напряжения в деталях конструкции не должны пре­вышать допускаемых напряжений для материала этих деталей. Мате­матические выражения условий прочности

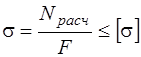- при растяжении-сжатии;

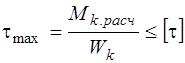- при кручении;

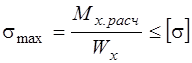- при изгибе.

Здесь s , t_max , s_max – максимальные расчетные напряжения в детали; N_расч , M_к.расч , M_х.расч – максимальные по абсолютному значению нормальная сила, крутящий момент, изгибающий момент в попереч­ном сечении; F, W_к , W_х – площадь, момент сопротивления кручению и момент сопротивления изгибу поперечного сечения.

Если на детали имеются участки с разными поперечными сече­ниями, то условия прочности составляются для каждого такого уча­стка.

В инженерной практике чаще всего решаются три типа задач проч­ности:

- проверка прочности (проверочный расчет);

- определение размеров поперечных сечений, обеспечивающих проч­ность (конструкторский расчет);

- определение допустимой (максимальной) нагрузки, при которой обеспечива­ется прочность.

Алгоритм решения этих задач включает в себя следующие шаги:

1. Выбор и изображение расчетной схемы;

2. Построение эпюр внутренних силовых факторов;

3. Определение расчетных значений внутренних силовых факторов;

4. Запись условий прочности;

5. Ответ на вопрос задачи.

Рассмотрим содержание этих шагов.*⁾

Выбор и изображение расчетной схемы

Расчетной схемой называется формализованное изображение рас­сматри­ваемой конструкции, освобожденное от несущественных для дан­ного расчета особенностей. Расчетная схема стержневой конст­рукции содержит стержни, кото­рые изображаются своей осевой ли­нией, нагрузки, опоры, необходимые для рас­чета размеры.

Построение эпюр внутренних силовых факторов

Алгоритм построения эпюр изложен в п. 3.2.

__________________________________________________________

*) Примеры практического использования алгоритма даны в разд. 4.4

Определение расчетных значений внутренних силовых факторов

В качестве расчетного, берется максимальное по абсолютной вели­чине зна­чения внутреннего силового фактора, имеющееся на его эпюре. Если стержни рас­четной схемы имеют разное поперечное се­чение, то для каждого стержня берется свое расчетное значение.

При расчете на прочность, при растяжении-сжатии стержней, изго­товленных из материалов не одинаково сопротивляющихся рас­тяже­нию и сжатию, берется два значения N_расч – максимальная рас­тяги­вающая и максимальная сжимающая.

Запись условий прочности

Если расчетная схема состоит из стержней одного сечения, то запи­сывается одно условие прочности. Если расчетная схема состоит из стержней разного сече­ния, то записывается условие прочности для каждого стержня.

При расчете стержней изготовленных из материалов не одина­ково сопро­тивляющихся растяжению-сжатию записываются отдель­ные условия прочности по растягивающим и сжимающим напряже­ниям.

Ответ на вопрос задачи

Если требуется проверить прочность конструкции, то вычисля­ются макси­мальные расчетные напряжения по формулам, состав­ляющим левую часть условий прочности и сравниваются с допускае­мыми. Прочность конструкции будет обес­печена, если все условия прочно­сти, записанные для данной конструкции, удовлетворяются, т.е. мак­симальные напряжения не превышают допускаемых.

Если требуется определить необходимые размеры сечения или допус­каемую нагрузку, то в условии прочности вместо знака "≤" ставится знак "=".

При растяжении-сжатии ;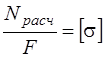

при кручении ; (*)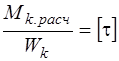

при изгибе .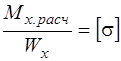

При определении размеров сечения в равенства (*) подставляют F, W_к , W_х выраженные через размеры сечения, а затем разрешают их отно­сительно размеров сечения. Подставляя в полученные выраже­ния численные значения вхо­дящих в них констант и переменных и, про­изводя необходимые математические действия, получают чис­ленное значение необходимых размеров сечения.

Если расчетная схема имеет участки с разными поперечными сече­ниями, то аналогичным образом определяют размеры всех уча­стков.

Если определяется допускаемая нагрузка, то в равенства (*) подстав­ляют N_расч , M_к.расч , M_х.расч , выраженные через внешнюю на­грузку q, Р , М. Разрешают полученные уравнения относительно внешней на­грузки и вычисляют её. Если в расчетной схеме имеются участки с разными попе­речными сечениями, то определяют допус­каемую на­грузку исходя из условия прочности каждого участка. Та­ким образом, получают столько значений допус­каемой нагрузки, сколько участков с различными сечениями в расчетной схеме. За от­вет задачи берут меньшее, из полученных значений допускаемой на­грузки.

Некоторые инженерные и учебные задачи прочности могут отли­чаться по своей постановке и цели от трех основных типов задач. В соответствии с этим ал­горитмы их решения также могут отличаться от алгоритма решения этих типов задач прочности.