Коэффициент корреляции

Коэффициент корреляции - это величина, которая может варьировать в пределах от +1 до — 1. В случае полной положительной корреляции этот коэффициент равен плюс 1, а при полной отрицательной - минус 1. На графике этому соответствует прямая линия, проходящая через точки пересечения значений каждой пары данных:

. Переменная 8

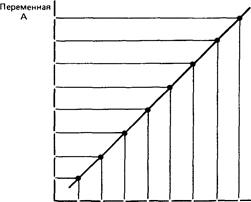
Полная положительная корреляция (г =+1)

308 Приложение Б

\

Переменная В

Полная отрицательная корреляция (/" ^-l)

В случае же если эти точки не выстраиваются по прямой линии, а образуют «облако», коэффициент корреляции по абсолютной величине становится меньше единицы и по мере округления этого облака прибли­жается к нулю:

' -0,30 r=0

В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.

В гуманитарных науках корреляция считается сильной, если ее коэффициент выше 0,60; если же он превышает 0,90, то корреляция считается очень сильной. Однако для того, чтобы можно было делать выводы о связях между переменными, большое значение имеет объем выборки: чем выборка больше, тем достовернее величина полученного коэффициента корреляции. Существуют таблицы с критическими значе­ниями коэффициента корреляции Браве - Пирсона и Спирмена для разного числа степеней свободы (оно равно числу пар за вычетом 2, т. е. п — 2). Лишь в том случае, если коэффициенты корреляции больше этих критических значений, они могут считаться достоверными. Так, для того чтобы коэффициент корреляции 0,70 был достоверным, в анализ должно быть взято не меньше 8 пар данных (г| = п — 2 = 6) при вычислении г (табл. В.4) и 7 пар данных (г| = и — 2 = 5) при вычислении г, (табл. 5 в дополнении 6.5). - ——-

Статистика и обработка данных