Математический анализ
РедакторР. В. Щадько
________________________________________________________Подписано в печать: Формат 84х60 1/16. Бум. офсет.
Печ. офс. Усл.-печ. 6,8 Тираж 100 экз.
Заказ № Цена договорная.
Донецкий национальный университет, Украина, 83055, г. Донецьк, ул. Университетская, 24.
[А1]
[А2]
Академия труда и социальных отношений
Красноярский филиал
Задания для выполнения
контрольной работы
по математическому анализу
для студентов заочной формы обучения
специальности «Финансы и кредит», «Бухгалтерский учет, анализ и аудит»
«Экономика труда»
Каждое задание контрольной работы содержит 20 вариантов. Номер своего варианта студент выбирает по последним двум цифрам номера зачетки, как остаток от деления на 20. Например, цифрам 34 соответствует 14 вариант (при делении на 20 получаем 1 целую и 14 в остатке), цифрам 65 – 5 вариант (при делении на 20 получаем 3 целых и 5 в остатке), цифрам 70 – 10 вариант (при делении на 20 получаем 3 целых и 10 в остатке), если остаток от деления равен 0, номер варианта 20.
Хотелось бы напомнить, что основной формой заочного обучения является самостоятельная работа студента над учебным материалом.
План самостоятельной работы студента
1. Изучить теоретический материал, используя конспекты лекций и рекомендуемую учебную литературу. Советуем обратить особое внимание на определения основных понятий, подробно разобрать примеры, которые поясняют определения. При изучении материала по учебнику полезно вести конспект, в который рекомендуем записывать определения, формулировки теорем, формулы и т.д.
2. Чтение учебника должно сопровождаться решением задач. При решении задач нужно обосновывать каждый этап решения, исходя из теоретических положений.
3. Выполнить контрольную работу.
При выполнении контрольной работы студент должен придерживаться следующих правил:
· работа выполняется в отдельной тетради, на обложке которой указаны: фамилия, имя, отчество студента; учебный шифр; номер учебной специальности; название дисциплины и номер контрольной работы;
· оформление каждой задачи начинается с формулировки ее условия (в соответствии с вариантом). Решение следует описывать подробно и аккуратно, поясняя все действия и делая необходимые чертежи;
· в контрольной работе должны быть решены все задачи строго в соответствии со своим вариантом.
Работа выполненная с нарушением этих правил не зачитывается и возвращается студенту. Без предъявления прорецензированных контрольных работ студент не допускается к сдаче зачета и экзамена.
4. Ответить на вопросы для самопроверки с целью закрепления и проверки качества усвоения изученного материала.
В помощь студентам-заочникам во время установочных и экзаменационных сессий проводятся лекционные и практические занятия. Вследствие ограниченного времени, лекции и практические занятия носят обзорный характер, поэтому на них рассматриваются самые важные и сложные темы.
Выражаем надежду на то, что данные советы и рекомендации будут полезны студенту и окажут ему помощь при изучении теоретического материала, выполнении контрольной работы и в процессе подготовки к экзамену.
Контрольная работа №2
Математический анализ
Задача 6.
Вычислить пределы функций, не пользуясь правилом Лопиталя.
6.1. a) 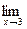
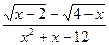 ; b)
; b) 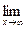
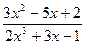 ; c)
; c) 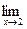
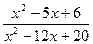 ; d)
; d) 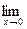
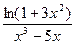 ;
;
6.2 . a) 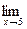
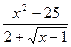 ; b)
; b) 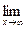
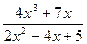 ; c)
; c) 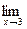
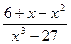 ; d )
; d ) 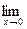
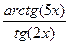 ;
;
6.3 a ) 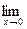
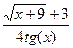 ; b )
; b ) 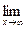
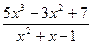 ; c )
; c ) 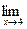
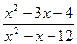 ; d )
; d ) 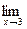
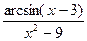 ;
;
6.4. a ) 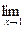
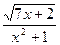 ; b )
; b ) 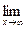
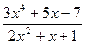 ; c )
; c ) 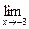
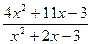 ; d )
; d ) 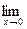
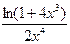 ;
;
6.5. a ) 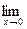
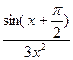 ; b )
; b ) 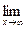
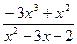 ; c )
; c ) 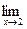
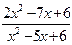 ; d )
; d ) 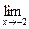
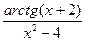 ;
;
6.6. a ) 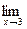
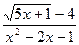 ; b )
; b ) 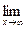
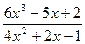 ; c )
; c ) 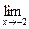
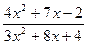 ; d )
; d ) 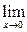
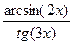 ;
;
6.7. a ) 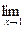
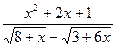 ; b )
; b ) 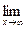
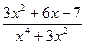 ; c )
; c ) 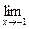
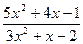 ; d )
; d ) 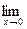
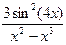 ;
;
6.8. a ) 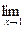
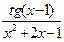 ; b )
; b ) 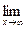
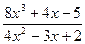 ; c )
; c ) 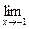
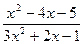 ; d )
; d ) 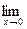
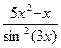
6.9. a ) 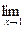
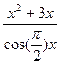 ; b )
; b ) 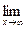

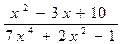 ; c )
; c ) 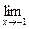
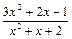 ; d)
; d) 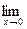
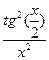
6.10. a ) 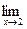
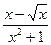 ; b )
; b ) 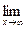
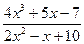 ; c )
; c ) 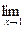
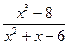 ; d )
; d ) 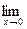
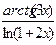 ;
;
6.11. a) 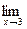
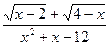 ; b)
; b) 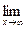
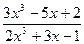 ; c)
; c) 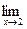
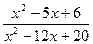 ; d)
; d) 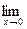
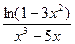 ;
;
6.12 . a) 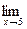
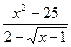 ; b)
; b) 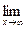
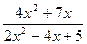 ; c)
; c) 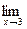
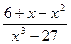 ; d )
; d ) 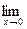
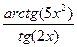 ;
;
6.13. a ) 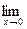
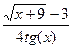 ; b )
; b ) 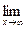
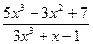 ; c )
; c ) 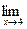
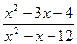 ; d )
; d ) 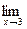
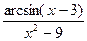 ;
;
6.14. a ) 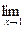
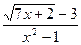 ; b )
; b ) 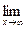
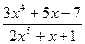 ; c )
; c ) 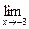
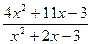 ; d )
; d ) 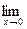
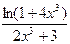 ;
;
6.15. a ) 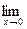
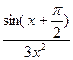 ; b )
; b ) 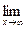
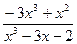 ; c )
; c ) 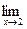
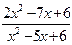 ; d )
; d ) 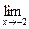
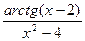 ;
;
6.16. a ) 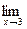
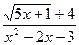 ; b )
; b ) 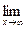
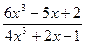 ; c )
; c ) 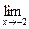
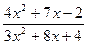 ; d )
; d ) 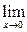
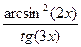 ;
;
6.17. a ) 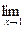
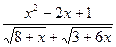 ; b )
; b ) 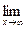
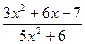 ; c )
; c ) 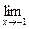
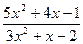 ; d )
; d ) 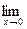
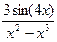 ;
;
6.18. a ) 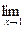
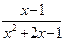 ; b )
; b ) 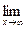
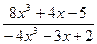 ; c )
; c ) 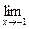
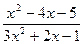 ; d )
; d ) 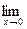
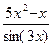
6.19. a ) 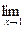
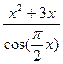 ; b )
; b ) 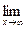

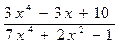 ; c )
; c ) 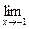
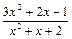 ; d)
; d) 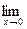
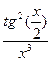
6.20. a ) 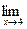
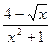 ; b )
; b ) 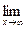
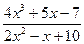 ; c )
; c ) 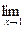
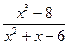 ; d )
; d ) 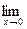
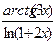 ;
;

Задача 7.
Задание а) Задана функция y=f(x) и два значения аргумента x  и x
и x  . Требуется:
. Требуется:
1) найти область непрерывности функции и установить, является ли данная функция непрерывной для каждого из заданных значений аргумента;
2) в случае разрыва функции сделать вывод о характере точки разрыва;
3) сделать схематический чертёж в окрестности точки разрыва.
Задание б)Найти точки разрыва функции и определить характер разрыва. Построить график функции.
7.1 a ) f(x)=2 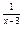 +1 , x
+1 , x  = 4, x
= 4, x  =3 ; b) f(x)=
=3 ; b) f(x)= 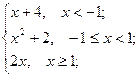
7.2 a ) f(x)= 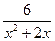 , x
, x  = 0 , x
= 0 , x  = 1 ; b ) f(x)=
= 1 ; b ) f(x)= 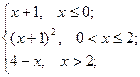
7.3 a) f(x)=4 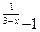 , x
, x  = 3 , x
= 3 , x  = 4 ; b ) f(x)=
= 4 ; b ) f(x)= 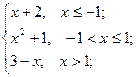
6.4 a) f(x)= 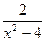 , x
, x  = 2 , x
= 2 , x  = 3 ; b ) f(x)=
= 3 ; b ) f(x)= 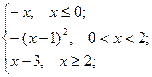
6.5 a) f(x)= 12 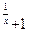 , x
, x  = 1 , x
= 1 , x  = 0 ; b ) f(x)=
= 0 ; b ) f(x)= 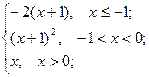
6.6 a) f(x)= 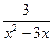 , x
, x  = 0 , x
= 0 , x  = 2 ; b ) f(x)=
= 2 ; b ) f(x)= 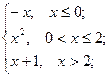
6.7 a) f(x)= 2 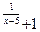 , x
, x  = 5 , x
= 5 , x  = 6 ; b ) f(x)=
= 6 ; b ) f(x)= 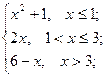
7.8 a) f(x)= 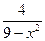 , x
, x  = 2 , x
= 2 , x  = 3 ; b ) f(x)=
= 3 ; b ) f(x)= 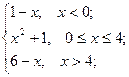
7.9 a) f(x)= 3 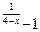 , x
, x  = 4 , x
= 4 , x  = 6 ; b ) f(x)=
= 6 ; b ) f(x)= 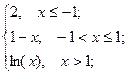
7.10 a) f(x)= 4 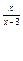 , x
, x  = 3 , x
= 3 , x  = 4 ; b ) f(x)=
= 4 ; b ) f(x)= 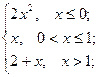
7.11 a) f(x)= 8 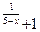 , x
, x  = 7 , x
= 7 , x  = 5 ; b ) f(x)=
= 5 ; b ) f(x)= 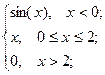
7.12 a) f(x)= 9 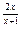 , x
, x  = -1 , x
= -1 , x  = 0 ; b ) f(x)=
= 0 ; b ) f(x)= 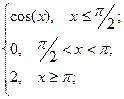
7.13 a) f(x)= 2 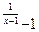 , x
, x  = 1 , x
= 1 , x  = 0 ; b ) f(x)=
= 0 ; b ) f(x)= 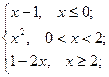
7.14 a) f(x)= 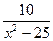 , x
, x  = -5 , x
= -5 , x  = 4 ; b ) f(x)=
= 4 ; b ) f(x)= 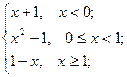
7.15 a) f(x)= 3 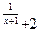 , x
, x  = -1 , x
= -1 , x  = 0 ; b ) f(x)=
= 0 ; b ) f(x)= 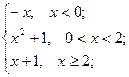
7.16 a) f(x)= 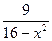 , x
, x  = 3 , x
= 3 , x  = 5 ; b ) f(x)=
= 5 ; b ) f(x)= 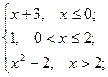
7.17 a) f(x)= 4 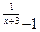 , x
, x  = -3 , x
= -3 , x  = -2 ; b ) f(x)=
= -2 ; b ) f(x)= 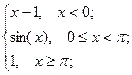
7.18 a) f(x)= 8 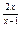 , x
, x  = 0 , x
= 0 , x  = 1 ; b ) f(x)=
= 1 ; b ) f(x)= 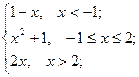
7.19 a) f(x)= 3 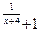 , x
, x  = -2 , x
= -2 , x  = -4 ; b ) f(x)=
= -4 ; b ) f(x)= 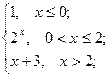
7.20 a) f(x)= 7 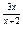 , x
, x  = -2 , x
= -2 , x  = 0 ; b ) f(x)=
= 0 ; b ) f(x)= 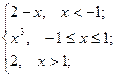
Задача 8.
Задача на применение функций одной переменной в экономике
Заданы функции спроса 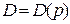 и предложения
и предложения 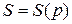 на товар в зависимости от цены
на товар в зависимости от цены 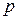 . Требуется:
. Требуется:
1) найти область определения и множество значений функций;
2) найти объем предложения и объем спроса товара по цене 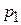 ; определить, что будет - избыточное предложение или избыточный спрос; вычислить выручку продавцов
; определить, что будет - избыточное предложение или избыточный спрос; вычислить выручку продавцов 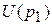 ;
;
3) найти равновесную цену 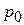 , равновесный объем продаж
, равновесный объем продаж 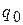 и выручку продавцов
и выручку продавцов 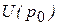 ;
;
4) построить графики функций 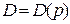 и
и 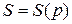 в одной системе координат, указать значение
в одной системе координат, указать значение 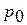 .
.
8.1. 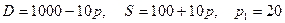
|
8.2. 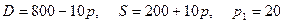
|
8.3. 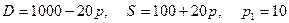
|
8.4. 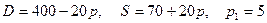
|
8.5. 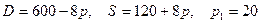
|
8.6. 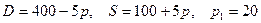
|
8.7. 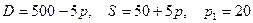
|
8.8. 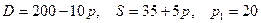
|
8.9. 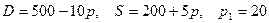
|
8.10. 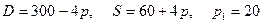
|
8.11. 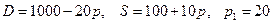
|
8.12. 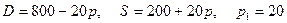
|
8.13. 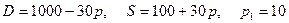
|
8.14. 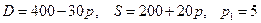
|
8.15. 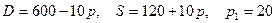
|
8.16. 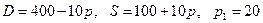
|
8.17. 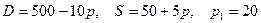
|
8.18. 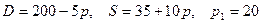
|
8.19. 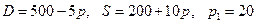
|
8.20. 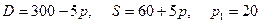
|
Задача 9.
Найти производные 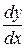 данных функций.
данных функций.
9.1. а) 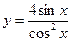 ; б)
; б) 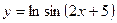
9.2. а) 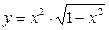 ; б)
; б) 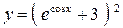
9.3. а) 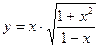 ; б)
; б) 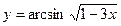 ;
;
9.4. а) 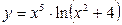 ; б)
; б) 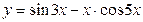
9.5. а) 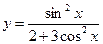 ; б)
; б) 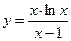 ;
;
9.6. а) 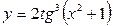 ; б)
; б) 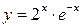
9.7. а) 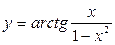 ; б)
; б) 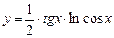
9.8. а) 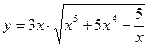 ; б)
; б) 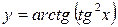
9.9. а) 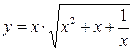 ; б)
; б) 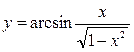
9.10. а) 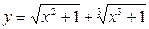 ; б)
; б) 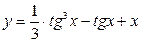
9.11. а) 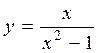 ; б)
; б) 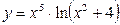
9.12. а) 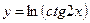 ; б)
; б) 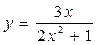
9.13. а) 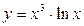 ; б)
; б) 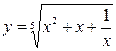
9.14. а) 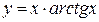 ; б)
; б) 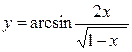
9.15. а) 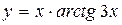 ; б)
; б) 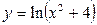
9.16. а) 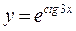 ; б)
; б) 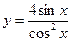
9.17. а) 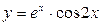 ; б)
; б) 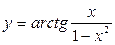
9.18. а) 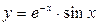 ; б)
; б) 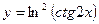
9.19. а) 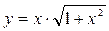 ; б)
; б) 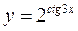
9.20. а) 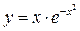 ; б)
; б) 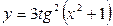
Задача 10.
Задача на экономические приложения производных функций одной переменной.
10.1. Поступления от реализации производственной продукции 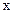 выражаются функцией
выражаются функцией 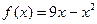 , а затраты, связанные с производством продукции в количестве
, а затраты, связанные с производством продукции в количестве 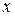 , записываются функцией
, записываются функцией 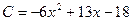 . Определите оптимальный объем производства, обеспечивающий максимум прибыли.
. Определите оптимальный объем производства, обеспечивающий максимум прибыли.
10.2. Найти эластичность функции спроса 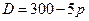 по цене и эластичность функции предложения
по цене и эластичность функции предложения 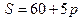 по цене при
по цене при 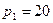 . Определить, на сколько процентов изменятся спрос и предложение, если цена увеличится на 5%..
. Определить, на сколько процентов изменятся спрос и предложение, если цена увеличится на 5%..
10.3. Затраты, связанные с производством продукции, определяются функцией 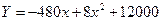 . Определите объем производства, обеспечивающий минимальные затраты. Дайте экономическое истолкование результату.
. Определите объем производства, обеспечивающий минимальные затраты. Дайте экономическое истолкование результату.
10.4. Объем 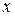 выпущенной продукции и выручка
выпущенной продукции и выручка 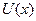 , полученная от реализации, заданы функцией
, полученная от реализации, заданы функцией 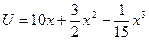 . Найдите, при каком объеме продукции выручка минимальна. Вычислите предельную выручку.
. Найдите, при каком объеме продукции выручка минимальна. Вычислите предельную выручку.
10.5. Цена на товар составляет 250 руб., издержки производства этого товара равны 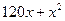 , где
, где 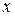 - число единиц произведенного товара. Найти, при каком количестве товара функция прибыли принимает максимальное значение.
- число единиц произведенного товара. Найти, при каком количестве товара функция прибыли принимает максимальное значение.
10.6. Издержки производства продукции определяются функцией 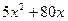 , где
, где 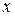 - число единиц произведенной за месяц продукции. Продукция продается по цене 280 руб. за изделие. Сколько изделий нужно произвести и продать, чтобы прибыль была максимальна?
- число единиц произведенной за месяц продукции. Продукция продается по цене 280 руб. за изделие. Сколько изделий нужно произвести и продать, чтобы прибыль была максимальна?
10.7. Количество произведенной за день продукции 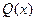 зависит от числа рабочих в сборочном цехе следующим образом:
зависит от числа рабочих в сборочном цехе следующим образом: 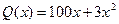 , где
, где 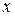 - число рабочих. Вычислить значение прироста выработки за неделю, вызванное добавлением одного рабочего.
- число рабочих. Вычислить значение прироста выработки за неделю, вызванное добавлением одного рабочего.
10.8. Вычислить предельную выручку, если известны уравнение спроса 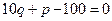 и значение цены
и значение цены 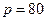 на продукцию (
на продукцию ( 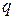 - количество продукции,
- количество продукции, 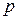 - цена продукции). Что она показывает?
- цена продукции). Что она показывает?
10.9 . Производитель реализует продукцию по цене 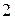 ден. ед. за единицу, а общие издержки равны
ден. ед. за единицу, а общие издержки равны 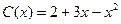 ден. ед., где
ден. ед., где 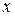 - количество продукции. Известно, что наибольшая прибыль достигается при выпуске 0,5 ед. продукции. Чему равны полный доход
- количество продукции. Известно, что наибольшая прибыль достигается при выпуске 0,5 ед. продукции. Чему равны полный доход 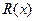 и общие издержки
и общие издержки 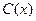 при оптимальном плане выпуска продукции?
при оптимальном плане выпуска продукции?
10.10. Вычислить предельную выручку, если известно уравнение спроса 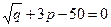 и значение цены
и значение цены 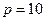 на некоторую продукцию (
на некоторую продукцию ( 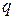 - количество продукции,
- количество продукции, 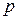 - цена продукции).
- цена продукции).
10.11. Вычислить эластичность функции спроса 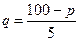 в точке
в точке 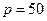 (
( 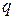 - количество продукции,
- количество продукции, 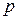 - цена продукции). Дать экономическое истолкование результату. Вычислить процентное изменение спроса, если цена уменьшилась на 2%.
- цена продукции). Дать экономическое истолкование результату. Вычислить процентное изменение спроса, если цена уменьшилась на 2%.
10.12. Задана зависимость 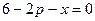 , связывающая количество продукции
, связывающая количество продукции 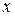 и цену
и цену 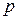 товара. Постоянные издержки производства составляют
товара. Постоянные издержки производства составляют 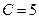 ден.ед., а переменные затраты на одну единицу продукции равны 2 ден.ед. Запишите функции дохода
ден.ед., а переменные затраты на одну единицу продукции равны 2 ден.ед. Запишите функции дохода 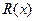 , общих издержек
, общих издержек 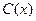 и прибыли
и прибыли 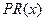 . Постройте графики функций
. Постройте графики функций 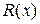 ,
, 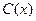 ,
, 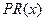 .
.
10.13. Зависимость спроса от цены выражается формулой 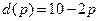 . Запишите функцию выручки от цены. При каких значениях цены выручка возрастает? Вычислите эластичность спроса на товар по цене
. Запишите функцию выручки от цены. При каких значениях цены выручка возрастает? Вычислите эластичность спроса на товар по цене 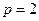 , дайте экономическое истолкование.
, дайте экономическое истолкование.
10.14. Зависимость спроса от цены выражается формулой 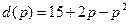 . Вычислите эластичность спроса на товар по цене
. Вычислите эластичность спроса на товар по цене 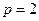 , дайте экономическое истолкование. Постройте график предельного спроса. Запишите функцию выручки от цены. При каких значениях цены выручка убывает?
, дайте экономическое истолкование. Постройте график предельного спроса. Запишите функцию выручки от цены. При каких значениях цены выручка убывает?
10.15. Пусть 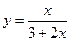 есть функция Торнквиста спроса потребителей
есть функция Торнквиста спроса потребителей 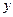 на товары первой необходимости в зависимости от дохода
на товары первой необходимости в зависимости от дохода 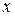 . Найдите эластичность
. Найдите эластичность 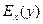 при
при 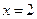 , дайте экономическое истолкование полученному результату.
, дайте экономическое истолкование полученному результату.
10.16. Дана функция спроса 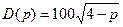 от цены товара
от цены товара 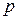 . Составить функцию выручки. Вычислить эластичность функции спроса в точке
. Составить функцию выручки. Вычислить эластичность функции спроса в точке 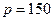 и дать экономическое истолкование результату. Как повлияет изменение цены на выручку?
и дать экономическое истолкование результату. Как повлияет изменение цены на выручку?
10.17. Предприятие производит 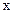 ед. продукции в месяц и реализует ее по цене
ед. продукции в месяц и реализует ее по цене 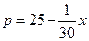 . Суммарные издержки производства составляют
. Суммарные издержки производства составляют 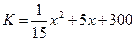 . Определите, при каком объеме производства прибыль предприятия будет максимальной.
. Определите, при каком объеме производства прибыль предприятия будет максимальной.
10.18. Производитель реализует свою продукцию по цене 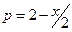 ден. ед. за единицу продукции, а издержки задаются функцией
ден. ед. за единицу продукции, а издержки задаются функцией 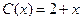 , где
, где 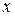 - объем выпущенной продукции. Найдите оптимальный объем выпуска продукции и соответствующую прибыль.
- объем выпущенной продукции. Найдите оптимальный объем выпуска продукции и соответствующую прибыль.
10.19. Поступления от реализации производственной продукции 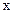 выражаются функцией
выражаются функцией 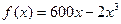 , а затраты, связанные с производством продукции
, а затраты, связанные с производством продукции 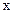 , записываются функцией
, записываются функцией 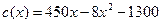 . Определите оптимальный объем производства, обеспечивающий максимум прибыли.
. Определите оптимальный объем производства, обеспечивающий максимум прибыли.
10.20. Производитель реализует свою продукцию по цене 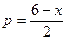 ден.ед. за единицу продукции, а издержки задаются функцией
ден.ед. за единицу продукции, а издержки задаются функцией 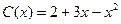 , где
, где 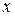 - объем выпущенной продукции. Найдите оптимальный объем выпуска продукции и соответствующую прибыль.
- объем выпущенной продукции. Найдите оптимальный объем выпуска продукции и соответствующую прибыль.
Задача 11.
Найти наименьшее и наибольшее значения линейной функции Z=C1 х+ C2 y + C0 в области решений системы линейных неравенств.
11.1 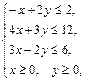
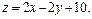
11.2 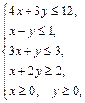
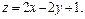
11. 3 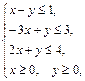
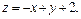
11.4 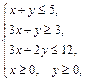
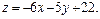
11.5 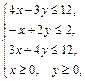
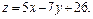
11.6 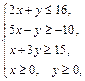
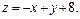
11.7 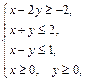
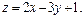
11.8 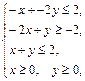
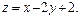
11.9 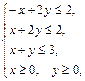
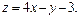
11.10 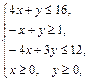
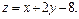
11.11 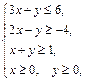
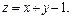
11.12 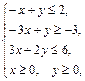
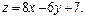
11.13 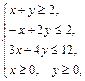
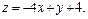
11.14 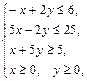
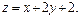
11.15 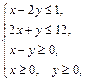
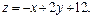
11.16 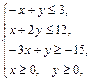
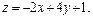
11.17 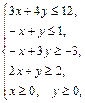
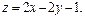
11.18 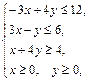
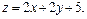
11.19 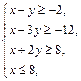
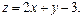
11.20 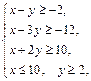
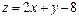
Дата добавления: 2014-12-08; просмотров: 1682;
