Задача 12.

Задача на экономические приложения производных функций нескольких переменных

12.1.Затраты фирмы по выпуску 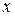изделий первого вида составляют 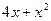ден.ед., а по выпуску 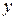изделий второго вида 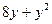ден. ед.

1) Составьте функцию 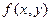общих затрат на производство всех изделий и вычислите затраты фирмы по выпуску двух изделий первого вида и одного изделий второго вида.

2) Определите вид линий уровня и постройте одну из них при .

3) Вычислите эластичности затрат по каждому виду изделий, если 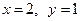, и дайте им экономическое истолкование.

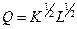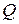12.2.Производственная деятельность фирмы описывается функцией Кобба-Дугласа , где - величина выпуска продукции, 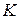- число единиц оборудования (капитал) и - численность работающих (труд).

1) Составьте функцию издержек фирмы, если стоимость ед. фактора 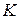равна 4 ден.ед., а стоимость ед. фактора 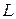равна 1 ден.ед.

2) Решите задачу определения максимального выпуска продукции, который может обеспечить фирма, полностью истратив все средства 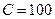ден.ед.

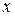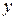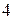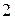12.3.Предприятие работает по первой технологии часов и по второй часов, выпуская за час работы по каждой технологии продукцию стоимостью ден. ед. и ден. ед. Производственные расходы за 1 час работы составляют ден. ед. и ден. ед.

1) Составьте функции дохода, общих расходов, прибыли и вычислите прибыль фирмы за время работы по первой технологии 2 часа, а по второй 1 час.

2) Определите вид линий уровня функции прибыли и постройте их.

3) Вычислите эластичности функции прибыли по каждой технологии за время работы по первой технологии 2 часа, а по второй 1 час и дайте им экономическое истолкование.

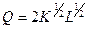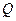12.4.Производственная деятельность фирмы описывается функцией Кобба-Дугласа , где - величина выпуска продукции, 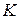- число единиц оборудования (капитал) и - численность работающих (труд).

1) Составьте функцию издержек фирмы, если стоимость единицы 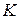равна 1 ден. ед., а стоимость единицы равна 2 ден. ед.

2) Определите наименьшие издержки при выпуске количества продукции .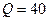

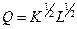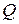12.5.Производственная деятельность фирмы описывается функцией Кобба-Дугласа , где - величина выпуска продукции, 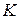- число единиц оборудования (капитал) и - численность работающих (труд).

1) Составьте функцию издержек фирмы, если стоимость единицы 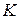равна 2 ден. ед., а стоимость единицы равна 4 ден. ед.

2) Найдите максимальный выпуск продукции, который может обеспечить фирма, полностью истратив все имеющиеся средства 60 ден. ед.

12.6. Дана производственная функция фирмы 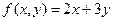, где 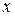, 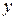- объемы используемых ресурсов. Известны рыночные цены продукции и ресурсов: , , .

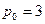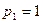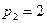1) Составьте функции дохода 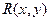, издержек 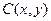и прибыли 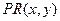и вычислите прибыль фирмы при использовании 2 ед. первого ресурса и 3 ед. второго ресурса.

2) Определите вид линий уровня функции прибыли и постройте ее при , .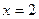

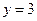3) Вычислите эластичности прибыли по каждому виду ресурсов при 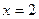, 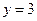и дайте им экономическое истолкование.

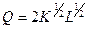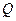12.7. Производственная деятельность фирмы описывается функцией Кобба-Дугласа , где - величина выпуска продукции, 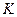- число единиц оборудования (капитал) и 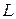- численность работающих (труд).

1) Составьте функцию издержек фирмы, если стоимость единицы 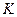равна 4 ден.ед., а стоимость единицы равна 4 ден.ед.

2) Определите наименьшие издержки при выпуске 30 единиц продукции.

12.8. Дана производственная функция фирмы , где 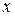, 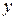- объемы используемых ресурсов. Известны рыночные цены продукции и ресурсов: , , .

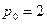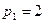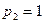1) Составьте функции дохода 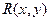, издержек 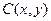и прибыли 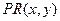и вычислите прибыль при использовании 3 ед. первого ресурса и 2 ед. второго ресурса.

2) Определите вид линий уровня функции прибыли и постройте ее при , .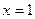

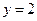3) Вычислите эластичности прибыли по каждому виду ресурсов при 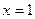, 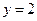и дайте им экономическое истолкование.

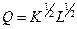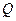12.9. Производственная деятельность фирмы описывается функцией Кобба-Дугласа , где - величина выпуска продукции, 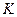- число единиц оборудования (капитал) и - численность работающих (труд).

1) Составьте функцию издержек фирмы, если стоимость единицы 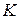равна 1 ден.ед., а стоимость единицы равна 4 ден. ед.

2) Определите максимальный выпуск продукции, который может обеспечить фирма, полностью истратив все имеющиеся средства 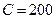ден.ед.

12.10. Пусть 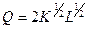- производственная функция фирмы, связывающая ресурсы (капитал 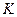, труд ) и выпуск продукции .

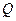1) Сколько единиц продукции выпускает фирма при технологическом способе производства 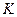= 10, = 40?

2) Постройте изокванту для выпуска продукции объемом Q (10, 40).

3) Найдите эластичности производственной функции при K=5, L=10 и дайте им экономическое истолкование.

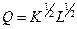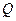12.11. Производственная деятельность фирмы описывается функцией Кобба-Дугласа , где - величина выпуска продукции, 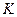- число единиц оборудования (капитал) и - численность работающих (труд).

1) Составьте функцию издержек фирмы, если стоимость единицы фактора 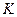равна 3 ден. ед., а стоимость единицы фактора равна 3 ден. ед.

2) Найдите максимальный выпуск продукции, который может обеспечить фирма, полностью истратив все имеющиеся средства 50 ден. ед.

12.12. Затраты на единицу продукции и 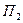составляют 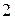и ден. ед.

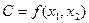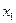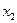1) Составьте функцию издержек , где , - объемы продукции и .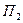

2) Постройте линию уровня, проходящую через точку 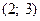,дайте экономическое истолкование.

3) Найдите эластичности издержек по каждому виду продукции при , дайте результатам экономическое истолкование.

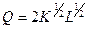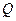12.13. Производственная деятельность фирмы описывается функцией Кобба-Дугласа , где - величина выпуска продукции, 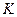- число единиц оборудования (капитал) и - численность работающих (труд).

1) Составьте функцию издержек фирмы, если стоимость ед. фактор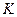а равна 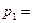1 ден. ед., а стоимость ед. фактора равна 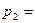2 ден. ед.

2) Определите наименьшие издержки при выпуске количества продукции .

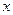12.14.Общие издержки производства заданы функцией , где и 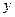- количество товаров 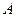и 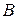. Общее количество произведенной продукции должно быть равно 500 ед.

1) Сколько единиц товара 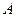и 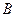нужно производить, чтобы издержки на их изготовление были наименьшими?

2) Постройте линию уровня функции, соответствующую наименьшим затратам.

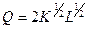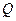12.15. Производственная деятельность фирмы описывается функцией Кобба-Дугласа , где - величина выпуска продукции, 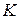- число единиц оборудования (капитал) и - численность работающих (труд).

1) Составьте функцию издержек фирмы, если стоимость единицы 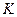равна 1 ден. ед., а единицы фактора равна 2 ден. ед.

2) Определите наименьшие издержки при выпуске количества продукции .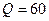

12.16Определить минимальную себестоимость продукции, если производственная функция себестоимости от факторов производства 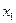и 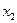определяется моделью 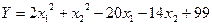, а ограничение на факторы 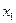и 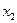имеет вид .

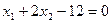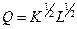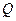12.17.Производственная деятельность фирмы описывается функцией Кобба-Дугласа , где - величина выпуска продукции, 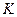- число единиц оборудования (капитал) и - численность работающих (труд).

1) Составьте функцию издержек фирмы, если стоимость ед. фактора 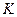равна 4 ден. ед., а стоимость ед. фактора равна 2 ден. ед.

2) Решите задачу определения максимального выпуска продукции, который может обеспечить фирма, полностью истратив все средства 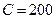ден. ед.

12.18.Фирма выпускает продукцию двух видов, при этом затраты составляют 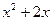ден. ед. на изготовление 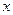ед. продукции и 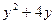ден. ед. на изготовление 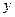ед. продукции 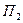. Рыночная цена единицы продукции равна соответственно 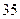и 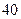ден. ед.

1) Составьте функции дохода, издержек и прибыли.

2) Вычислите прибыль и эластичности прибыли по каждому виду продукции при изготовлении 1 единицы и 2 единиц 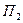, дайте им экономическое истолкование.

3) Постройте соответствующую линию уровня функции издержек и дайте ей экономическое истолкование.

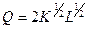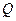12.19.Производственная деятельность фирмы описывается функцией Кобба-Дугласа , где - величина выпуска продукции, 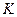- число единиц оборудования (капитал) и - численность работающих (труд).

1) Составьте функцию издержек фирмы, если стоимость единицы 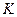равна 2 ден. ед., а единицы фактора равна 1 ден. ед.

2) Определите наименьшие издержки при выпуске количества продукции .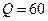

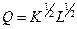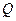12.20.Производственная деятельность фирмы описывается функцией Кобба-Дугласа , где - величина выпуска продукции, 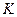- число единиц оборудования (капитал) и - численность работающих (труд).

1. Составьте функцию издержек фирмы, если стоимость ед. фактор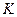а равна 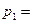2 ден. ед., а стоимость ед. фактора равна 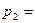4 ден. ед.

2. Найдите максимальный выпуск продукции, который может обеспечить фирма, полностью истратив все имеющиеся средства 60 ден. ед.

Вопросы для самопроверки и подготовки к экзамену

1. Что называется функцией? Какие существуют способы задания функций? Приведите примеры. Перечислите основные элементарные функции, постройте их графики.
2. Какая функция называется четной, нечетной? Приведите примеры. Какими особенностями обладают графики четной, нечетной функций?
3. Какая функция называется периодической? Приведите примеры.
4. Дайте определение предела функции в точке
5. Дайте определение бесконечно мало функции. Приведите примеры. Перечислите свойства бесконечно малых функций.
6. Дайте определение бесконечно большой функции. Перечислите свойства бесконечно больших функций. Какая связь существует между бесконечно большими и бесконечно малыми функциями?
7. Запишите определение непрерывной в точке функции. Сформулируйте необходимое и достаточное условие непрерывности.
8. Какая точка называется точкой разрыва функции? Приведите примеры функций, имеющих точки разрыва. Постройте графики разрывных функций.
9. Сформулируйте основные теоремы о функциях, непрерывных в точке, непрерывных на отрезке.
10. Дайте определение асимптоты. Как находятся вертикальные наклонные асимптоты?
11. Дайте определение производной функции в точке. Каков геометрический и механический смысл производной?
12. Запишите основные правила нахождения производной
13. Что называется дифференциалом функции? Каков геометрический смысл дифференциала? Какая функция называется дифференцируемой?
14. Сформулируйте необходимое условие существования экстремума функции одной переменной. Прочему это условие не является достаточным? Сформулируйте достаточные условия существования экстремума.
15. Запишите алгоритм нахождения наибольшего и наименьшего значений функции на отрезке. Сформулируйте теоремы, на которые он опирается.
16. Как найти точки перегиба функции?
17. Дайте определение функции двух, трех переменных. Что называется областью определения функции двух переменных?
18. Приведите примеры частного и полного приращений функции двух переменных
19. Дайте определение частной производной. Дайте определение полного дифференциала функции нескольких переменных
20. Запишите формулы для нахождения производной по направлению
21. Что показывает градиент функции? Какова связь между градиентом функции и производной по направлению?
22. Сформулируйте необходимое и достаточное условия экстремума функции двух переменных.
23. Запишите алгоритм нахождения наибольшего и наименьшего значений функции двух переменных в замкнутой области.