МНОГОЗНАЧНЫЕ ЛОГИКИ
Если в двузначной логике высказывание бывает истинным или ложным, то в многозначных логиках число значений истинности аргументов и функций может быть любым конечным и даже бесконечным. В настоящем приложении отрицание обозначается через N x или
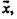 конъюнкция — через Кху или
конъюнкция — через Кху или 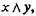 нестрогая дизъюнкция —через Аху или
нестрогая дизъюнкция —через Аху или 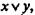 материальная импликация — через Сху или
материальная импликация — через Сху или 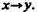 Значения функции от аргумента а будем записывать так: [д]. Тавтологией (или общезначимой) называется формула, которая при любых комбинациях значений входящих в нее переменных принимает значение «истина» (чаще всего в рассматриваемых системах «истина» обозначается цифрой 1).
Значения функции от аргумента а будем записывать так: [д]. Тавтологией (или общезначимой) называется формула, которая при любых комбинациях значений входящих в нее переменных принимает значение «истина» (чаще всего в рассматриваемых системах «истина» обозначается цифрой 1).
Развитие многозначных логик, по нашему мнению, подтверждает мысль, что истина всегда конкретна, а также положение об относительном характере конкретно-научных знаний: то, что является тождественно-истинным в одной логической системе, не оказывается тождественно-истинным в другой.
Трехзначная система Лукасевича29
Трехзначная пропозициональная логика была построена Я. Лукасевичем в 1920 г. В ней «истина» обозначается 1, «ложь» — 0, «нейтрально» — 1/2 . В качестве основных функций взяты отрицание (обозначается Nx) и импликация (Сху); производными являются конъюнкция (Кху) и дизъюнкция (Аху). Тавтология принимает значение 1.
Отрицание и импликация соответственно определяются матрицами (табл. 13, 14) и равенствами так:
Таблица 13
| х | Nx |
| ½ | ½ |
Таблица 14
| х / у | 1/2 | ||
| ½ | ½ | ½ |
1) [Nx]=l-[x];2) [Сху] = 1, если 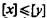 ; 3) [Сху] = 1-[x]+[у], если [x]>[у], или в общем виде: 4)[Сху]=min (1,1 — [x]+[у]).
; 3) [Сху] = 1-[x]+[у], если [x]>[у], или в общем виде: 4)[Сху]=min (1,1 — [x]+[у]).
Конъюнкция определяется как минимум значений аргументов: [Kxy]=min ([x], [у]); дизъюнкция — как максимум значений х и у: [Аху]= тах ([x], [у]).
На основе данных определений отрицания, конъюнкции и дизъюнкции в системе Лукасевича не будут тавтологиями (законами логики) закон непротиворечия и закон исключенного третьего двузначной логики, а также и отрицания законов непротиворечия и исключенного третьего. Поэтому логика Лукасевича не является отрицанием двузначной логики. В логике Лукасевича тавтологиями являются правило снятия двойного отрицания, все четыре правила де Моргана и правило контрапозиции: Не являются тавтологиями правила приведения к абсурду 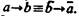 двузначной логики:
двузначной логики: 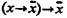 и
и 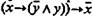 (т. е. если из х вытекает противоречие, то из этого следует отрицание х).Это можно доказать, взяв [х] = 1/2 и [у] = 1/2 .
(т. е. если из х вытекает противоречие, то из этого следует отрицание х).Это можно доказать, взяв [х] = 1/2 и [у] = 1/2 .
В системе Лукасевича не являются тавтологиями и некоторые формулы, структурно выражающие правильные дедуктивные умозаключения традиционной логики, формализованные средствами алгебры логики, а именно modus tollens, простая деструктивная дилемма, а также формулы разделительно-категорического силлогизма с нестрогой дизъюнкцией.
Все тавтологии логики Лукасевича являются тавтологиями в двузначной логике, ибо если отбросить значение 1/2, то в логике Лукасевича и в двузначной логике определения функций конъюнкции, дизъюнкции, импликации и отрицания соответственно совпадут. Но так как в логике Лукасевича имеется третье значение истинности — 1/2 , то не все тавтологии двузначной логики являются тавтологиями в логике Лукасевича.
Дата добавления: 2014-12-08; просмотров: 955;
