Математические модели объектов диагностирования
Математические модели – это математические формулы, описывающие изменение диагностического параметра в зависимости от пробега.
Наиболее распространенная математическая модель предложена В.М.Михлиным.
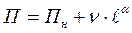 (1.4.)
(1.4.)
где П – величина диагностического параметра;
Пн – начальный диагностический параметр (у нового агрегата);
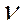 - коэффициент, характеризующий скорость изменения диагностического параметра;
- коэффициент, характеризующий скорость изменения диагностического параметра;
α - показатель степени, который определяет характер кривой;
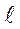 - пробег.
- пробег.
Математические модели применяются для прогнозирования.
Под прогнозированием технического состояния ТМО (рис. 1.8) понимают определение срока его исправной работы до возникновения предельного состояния, обусловленного технической документацией. Оценку технического состояния в прошлом (например, для выявления причины аварийного отказа, повлекшего за собой дорожно-транспортное происшествие) называют ретроспекцией.
Рассмотрим пример составления прогноза.
Определить пробег автомобиля, при котором потребуется провести предупредительный ремонт главной передачи, если предельное значение суммарного углового люфта в главной передаче равно 400, начальное значение этого параметра у нового автомобиля равно 100; скорость изменения люфта равна 0,2град/1000 км., а показатель степени a=1.
Решение:
из выражения (1.4.) следует, что 
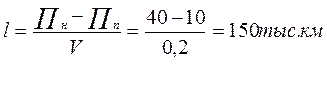



 П
П


Пп
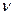
Пн
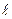
Рис. 1.8. Прогнозирование технического состояния
Дата добавления: 2014-12-08; просмотров: 1579;
