Норматива

Методика определения допустимого диагностического норматива (Пд) сводится к установлению допускаемого отклонения Д. Его можно определить

двумя методами: по совокупности реализаций и по плотностям распределений величин параметра исправных и неисправных объектов.

Сущность методики определения Пд по совокупности реализаций заключается в оптимизации Д по критерию минимума суммарных удельных затрат на ремонт и профилактику:

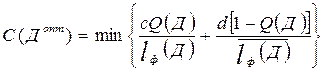(1.5.)

где с и d – стоимости, соответственно, ремонта и профилактики;

Q(Д) – вероятность отказа;

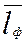(Д) – средний фактический ресурс до восстановления (ремонта или профилактики).

При увеличении Д возрастает вероятность отказа; в каждом цикле контроля эта вероятность равна:

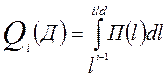(1.6.)

где i – порядковый номер диагностирования;

П (l) – известная плотность распределения наработки до предельного значения, а величина 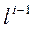определяется из подобия фигур Пп АО и ДВО (при линейных реализациях – прямоугольных треугольников), (рис.1.9.).

Соответственно возрастает и общая вероятность отказа, равная

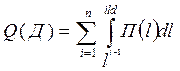(1.7.)

С другой стороны, при снижении Д, а следовательно, и уменьшении числа отказов, возрастает число преждевременных профилактических воздействий, в результате чего удельные суммарные затраты тоже удельных затрат на ремонт и профилактику будет растут. Таким образом, существует оптимальное значение Допт, при котором сумма минимальна.

Метод определения Пд по плотностям распределения диагностических параметров исправных и неисправных объектов базируется на определении такого норматива Пд, при котором суммарные потери от ошибок первого и второго рода будут минимальны. Ошибки первого рода – пропуск неисправности, ошибки второго рода – ложная неисправность.

ilⁱ_д

l_д^i-1

А

	ДД

В

l_д l_д l_д l_д

1 2 3 4 наработка, l

Рис. 1.9. Схема формирования Д при наличии совокупности реализации изменения диагностического параметра П (l):

Q1 ,Q2 – вероятности отказов на соответствующих пробегах.

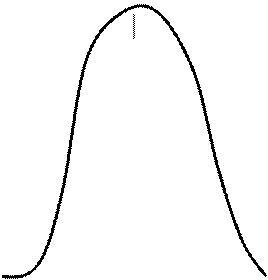
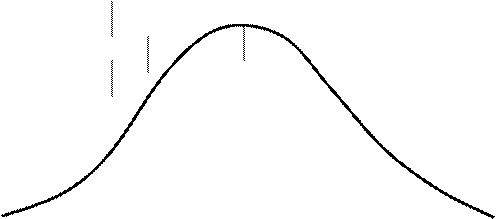
Если Пн<П<Пд, то объект считается исправным. При этом возникают ошибки первого рода, вероятность которых будет равна (рис. 1.10.).

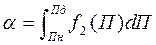(1.8.)

Потери от каждой ошибки первого рода будут равны c-d

Если П>Пд, то объект неисправен. Вероятность ошибки второго рода (рис. 1.10.) составит

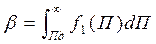(1.9)

а потери от каждой ошибки будут равны стоимости излишней профилактики d.

Средние суммарные потери от ошибок обоих родов составят:

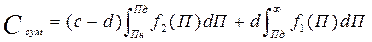(1.10.)

f(П)

f1(П)

α

f2(П)

β

Пн П1 Пд П2 П

Рис. 1.10. Методика определения допустимого норматива Пд по потерям от ошибок первого (a) и второго (b) рода:

f₁(П) и f2 (П) – плотности распределения параметров у исправных и у неисправных объектов и соответствующие им средние значения П₁ и П₂ ;

П_н и П_д – начальное и допустимое значения параметра.