МАТЕМАТИКА В АРТИЛЛЕРИИ

Вы убедились в том, что артиллеристу на поле боя приходится решать ряд математических задач. Вероятно, эти задачи показались вам очень простыми, и вам кажется странным, почему в артиллерии придают такое большое значение математике, почему принято говорить, что хорошими офицерами-артиллеристами могут стать только хорошие математики.

Не удивляйтесь — до сих пор мы выбирали для примеров только простейшие случаи, умышленно не затрудняли вас расчетами и вычислениями, чтобы понятнее была суть описанных приемов стрельбы. {336}

Но если вас интересует «артиллерийская математика», посмотрите, как выполняются расчеты и как решаются некоторые артиллерийские задачи.

Вы познакомились уже с тем, как командир батареи вычисляет коэфициент удаления. Рассмотрим подробнее, как решает он эту задачу. Для этого ему надо знать всего лишь два расстояния: командир — цель (его обозначают сокращенно буквами Дк — дальность от командира до цели) и батарея — цель (Дб — дальность от батареи до цели).

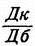Отношение называют коэфициентом удаления, обозначая его буквами Ку. Таким образом, первая формула, которой пользуется каждый артиллерист, имеет следующий вид:

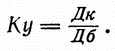
Вы уже видели на примере первой пристрелки, что применение этой формулы помогает правильно решить задачу.

Коэфициент удаления избавляет от лишних расчетов, помогает артиллеристам экономить снаряды и время. Но коэфициент удаления можно применять, когда командир не очень далеко ушел в сторону от батареи (угол при цели не более 5-00).

Когда командир находится в стороне от батареи, разрывы сойдут с его линии наблюдения при изменении установки прицела. Их надо удерживать на линии наблюдения, исправляя направление одновременно с изменением установки прицела.

Поправка направления, при помощи которой при изменении установки прицела удерживают разрыв на линии наблюдения, называется шагом угломера (рис. 302).

Этот шаг угломера можно тоже заранее рассчитать по формуле, известной каждому артиллеристу: угол при цели или так называемую поправку на смещение (ПС) надо разделить на количество сотен метров, которое содержится в расстоянии от батареи до цели, и тогда получится шаг угломера:

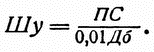
Проще всего вычислить шаг угломера, когда мы готовим данные по карте: угол при цели нетрудно измерить при помощи целлулоидного круга. {337}

И в других случаях нам тоже поможет математика. Мы можем, например, заменить карту несложным чертежом, который даст ответ на интересующий нас вопрос.

Кстати, этот же чертеж поможет нам сделать первый выстрел не наугад.

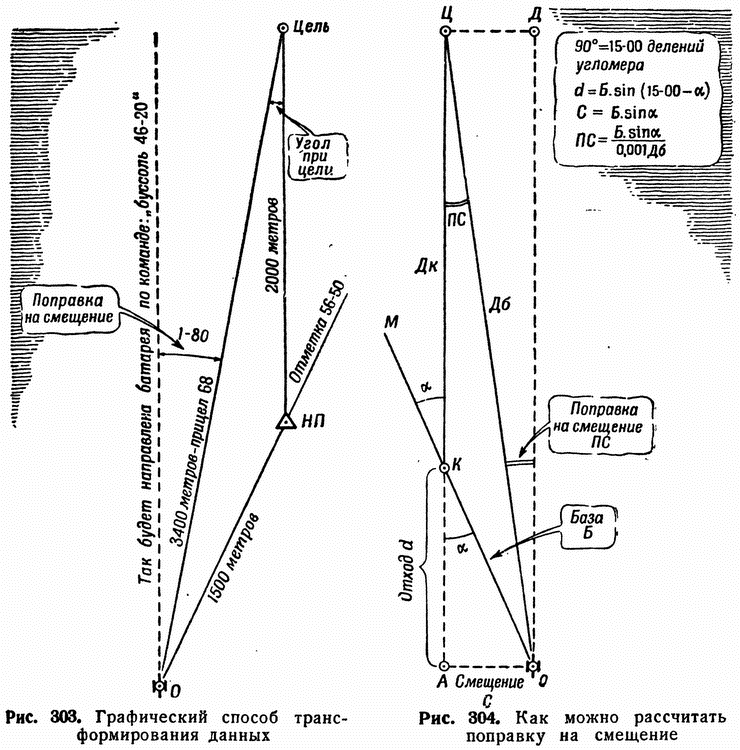
Возьмите листок бумаги и поставьте где угодно точку — это ваш наблюдательный пункт, или, сокращенно, НП (рис. 303). Проведите прямую линию вверх. На ней отложите в масштабе, которым вы задались (например, в одном сантиметре 200 метров), расстояние до цели, положим, 2000 метров. Здесь на чертеже окажется цель. Теперь подойдите к буссоли и направьте ее нолем в цель.

Но цель находится далеко и видна плохо. На помощь вам приходит монокуляр буссоли с шестикратным увеличением: оптическая ось монокуляра направлена всегда параллельно диаметру 30-0 буссоли (см. рис. 283).

Отпустите теперь магнитную стрелку и прочтите, против какого деления она остановилась. Пусть вы прочли 46-20. Это — азимут, или буссоль цели. Закрепите в этом положении угломерный круг и, освободив визирную трубку, направьте ее в сторону батареи. Против указателя визира прочтите отметку по батарее. Она равна, положим, 56-50.

Теперь наложите на ваш чертеж (см. рис. 303) целлулоидный круг: центром — на точку, которую вы приняли за наблюдательный пункт, нолем — в сторону цели. Прочертите на чертеже направление на батарею по отметке 56-50. Узнайте расстояние от вас до батареи (его можно промерить шагами, определить на глаз). Отложите это расстояние, например 1500 метров, в том масштабе, какой вы приняли для чертежа, и вы получите на чертеже точку — место батареи.

Соедините на чертеже точки «батарея» и «цель» прямой линией и, приложив линейку, измерьте дальность от батареи до цели.

Вы проделали не что иное, как решение геометрической задачи на построение треугольника по двум сторонам и углу между ними.

Несколько сложнее решить задачу — какую следует скомандовать буссоль, чтобы направить батарею в цель. Если вы скомандуете ту буссоль, какая получилась у вас на наблюдательном пункте, батарея, очевидно, будет направлена параллельно линии «наблюдательный пункт — цель» (см. рис. 303).

Надо довернуть батарею в сторону наблюдательного пункта на угол, который отчетливо виден на рисунке; этот угол и называется поправкой на смещение.

Каждому, кто знаком с геометрией, ясно, что поправка на смещение равна углу при цели.

На этот угол и надо довернуть батарею в сторону наблюдательного пункта.

В примере на рис. 303 батарею надо повернуть правее на величину угла при дели, который равен 1-80. Чтобы повернуть батарею правее, {338}

установку угломера или буссоли надо увеличить. Вот почему надо командовать буссоль не 46-20, а 46–20+1–80, то-есть 48-00.

Понятно, что, имея такой чертеж, можно легко подсчитать и коэфициент удаления и шаг угломера.

А можно обойтись и без чертежа: математика дает артиллеристам все формулы, нужные для расчетов.

Представьте себе взаимное расположение батареи (О), наблюдательного пункта (К) и цели (Ц) такое, как показано на рис. 304.

Для расчетов надо знать те же три величины, что и для решения задачи графически: во-первых, Дк во-вторых, расстояние от батареи до наблюдательного пункта (его принято называть базой и обозначать буквой Б); в-третьих, острый угол, составленный направлениями «наблюдательный пункт — цель» и «наблюдательный пункт — батарея». Этот угол обозначают греческой буквой «альфа» (a).

Опустите из точки О (батарея) перпендикуляр на продолжение линии КЦ (командир — цель). В прямоугольном треугольнике АOK нам {339} известны гипотенуза КО и угол АKO, который как вертикальный равен измеренному вами при помощи буссоли углу ЦКМ.

Зная эти две величины и тригонометрию, нетрудно найти катет АК (в артиллерии его называют «отход» и обозначают латинской буквой d): он равен базе KO, умноженной на косинус угла АKO или же на синус угла (90° – АKO). Это дает нам такую формулу:

d = Б sin (90° – a),

или

d = Б sin (15-00 – a),

А расстояние от батареи до цели без значительной ошибки можно принять в нашем случае равным КЦ + AK, то-есть расстоянию от командира до цели плюс отход:

Дб = Дк + d.

Таким образом, вы знаете теперь, какой надо назначить прицел.

Теперь нужно подсчитать поправку на смещение. Для этого достаточно изучить чертеж и формулы, приведенные на рис. 304.

В боевой обстановке надо пользоваться возможно более простыми формулами. Артиллеристы упрощают формулу, приведенную на рис. 304, и для полевых расчетов придают ей такой вид:

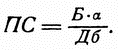
Они имеют полное право так поступать, потому что численно 1000 sin a » a, если только величину угла a выразить не в градусах, а в артиллерийских делениях; тогда можно допустить, что

sin 1-00 = 0,1;

sin 2-00 = 0,2

и т. д.

В этой простоте перехода от величины угла к величине его синуса заключается одно из немаловажных достоинств артиллерийской меры углов.

Теперь вы можете не только направить батарею в цель без всяких чертежей, но и рассчитать коэфициент удаления и шаг угломера.

Но этот способ не отличается высокой точностью: во-первых, составляя формулы, принимают, что ОЦ = АЦ, а это неточно; ошибка составляет тут нередко 100–200 метров; во-вторых, и это самое главное, расстояние Дк и базу Б чаще всего при этом способе определяют на глаз. Все это приводит к ошибкам, которые в среднем составляют 0-40 по направлению и 10 процентов по дальности.

Этот способ подготовки исходных данных для стрельбы артиллеристы применяют лишь тогда, когда важнее всего простота и скорость решения задачи, точностью же можно л поступиться: в бою это бывает нередко. {340}

Ну, а как быть, если нужна высокая точность подготовки данных для стрельбы?

Топография и математика и тут приходят на выручку: артиллеристы делают так называемое аналитическое определение направления и дальности стрельбы, по более точным и сложным формулам. Аналитическая геометрия, тригонометрия и таблицы логарифмов позволяют с очень большой точностью рассчитать направление стрельбы и дальности до цели.

Всем этим далеко не ограничиваются случаи применения математики в артиллерии. Артиллеристу она нужна буквально на каждом шагу. Даже из приведенных здесь примеров ясно, что артиллерист должен отлично знать и арифметику, и геометрию, и тригонометрию, и алгебру, и аналитическую геометрию. Этими науками артиллеристу иадо овладеть так хорошо, чтобы даже в бою, под огнем противника, он не ошибался в расчетах, уверенно и спокойно применяя нужные формулы. А для глубокого понимания теории стрельбы и науки о полете снаряда — баллистики — надо знать и высшую математику.