Для заочного отделения

В соответствии с учебным планом студенты заочного отделения должны выполнить контрольную работу по дисциплине «Эконометрика» и представить ее к сроку, установленному учебным графиком, но не позднее, чем за две недели до зачетно-экзаменационной сессии.

Выбор варианта осуществляется в таблице по первой букве фамилии студента.

Первая буква фамилии	Вариант контрольной работы	Первая буква фамилии	Вариант контрольной работы
А		П
Б		Р
В		С
Г		Т
Д		У
Е		Ф
Ж		Х
З		Ц
И		Ч
К		Ш
Л		Щ
М		Э
Н		Ю
О		Я

Вариант 1

1. Переменные x и y связаны соотношением y=a+bx. Дисперсия x равна Var(x). Чему равна ковариация между x и y?

2. Зависимость переменной y от переменной x задана таблицей x = 1 2 5 3 7 4 6 8 y = 3 3 3 3 3 3 3 3

Показать, что Cov(x,y)=0.

3. По некоторым данным о переменных x и y рассчитаны Var(x)=0.6, Var(y)=0.7, Cov(x,y)=0.4. Найти коэффициенты a и b регрессионного уравнения y=a+bx.

4. По некоторым данным о переменных x и y рассчитаны x_ср=0.5, (x²)_ср=0.6, y_ср=0.7, (y²)_ср=1.2,(xy)_ср=0.75. Найти коэффициент корреляции между x и y.

5. По таблице, содержащей 17 пар данных о переменных x и y, вычислены коэффициенты a=2.3, b=0.35, а также (x²_ср)=6.75 и r_xy=0.87. Найти 95% доверительные интервалы для a и b.

6. В каких из следующих выражений имеет место линейность по параметрам?

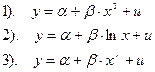
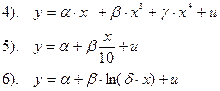
Вариант 2

Переменные x и y связаны соотношением y=a+bx. Дисперсия x равна Var(x). Чему равна дисперсия Var(y)?

2. Данные измерений переменной y в зависимости от переменной x приведены в таблице x = 1 2 5 3 7 4 6 8 y = 3 3 3 3 3 3 3 3 Предполагая линейную зависимость y от x: y=a+bx, построить регрессионное уравнение, т.е. найти коэффициенты a, b.

3. По некоторым данным о переменных x и y рассчитаны Var(x)=0.6, Var(y)=0.7, Cov(x,y)=0.4. Найти коэффициент корреляции r_xy между x и y.

4. По некоторым данным о переменных x и y рассчитаны x_ср=0.5, (x²)_ср=0.6, y_ср=0.7, (y²)_ср=1.2,(xy)_ср=0.75. Найти коэффициенты a и b регрессионного уравнения y=a+bx.

5. По таблице, содержащей 13 пар данных о переменных x и y, вычислены коэффициенты a=3.25, b=0.45, а также (x²_ср)=8.75 и r_xy=0.79. Найти 99% доверительные интервалы для a и b.

6. В каких из следующих выражений имеет место линейность по переменным?

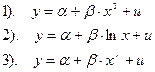
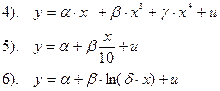
Вариант 3

1. Дисперсия переменной x равна Var(x)=D². Переменная y линейно зависит от x: y=a+bx. Чему равна дисперсия y?

2. Показать, что если переменные x и y связаны линейным соотношением y=a+bx, то коэффициент корреляции между x и y ρ(x,y)=±1.

3. Для переменной x = 0.5 1.5 2.5 3.5 4.5 рассчитать выборочную дисперсию.

4. Для переменных x и y, представленных ниже, рассчитать их средние величины, средние квадраты и средние произведения, а также коэффициент корреляции r_xy. x 0.5 1.5 2.5 3.5 4.5 y 1.2 2.8 5.1 7.3 8.8.

6. Какие из приведенных ниже уравнений допускают приведение к линейным регрессиям?

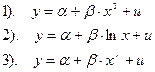
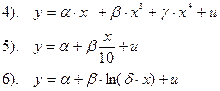
Вариант 4

Переменные x и y связаны соотношением y=a+bx. Дисперсия x равна Var(x). Чему равна дисперсия Var(y)?
Для переменных x 0.5 1.5 2.5 3.5 4.5 y 1.2 2.8 5.1 7.3 8.8 рассчитать выборочные дисперсии, выборочную ковариацию.
По некоторым данным о переменных x и y рассчитаны Var(x)=0.6, Var(y)=0.7, Cov(x,y)=0.4. Найти коэффициенты a и b регрессионного уравнения y=a+bx.
В некоторой таблице содержится информация о переменных y, x₁ и x₂. Предполагается построить линейную регрессионную модель 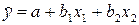. Расчеты дали значение для коэффициента корреляции между x₁ и x₂, равное 0.89. Следует ли придерживаться выбранной модели или выбрать иную?
По таблице, содержащей 13 пар данных о переменных x и y, вычислены коэффициенты a=3.25, b=0.45, а также (x²_ср)=8.75 и r_xy=0.79. Найти 99% доверительные интервалы для a и b.
Какие из приведенных ниже уравнений допускают приведение к линейным регрессиям?

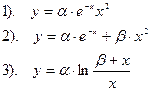
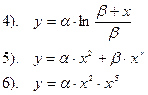
Вариант 5

Для переменных x 0.5 1.5 2.5 3.5 4.5 y 1.2 2.8 5.1 7.3 8.8 рассчитать выборочный коэффициент корреляции.
Дисперсия переменной x равна Var(x)=D². Переменная y линейно зависит от x: y=a+bx. Чему равна дисперсия y?

3. Данные измерений переменной y в зависимости от переменной x приведены в таблице x = 1 2 5 3 7 4 6 8 y = 3 3 3 3 3 3 3 3 Предполагая линейную зависимость y от x: y=a+bx, построить регрессионное уравнение, т.е. найти коэффициенты a, b.

По некоторым данным о переменных x и y рассчитаны x_ср=0.5, (x²)_ср=0.6, y_ср=0.7, (y²)_ср=1.2,(xy)_ср=0.75. Найти коэффициент корреляции между x и y.
По таблице, содержащей 17 пар данных о переменных x и y, вычислены коэффициенты a=2.3, b=0.35, а также (x²_ср)=6.75 и r_xy=0.87. Найти 95% доверительные интервалы для a и b.
Какие из приведенных ниже уравнений допускают приведение к линейным регрессиям?

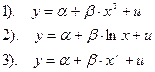
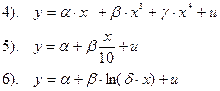
Вариант 6

Переменные x и y связаны соотношением y=a+bx. Дисперсия x равна Var(x). Чему равна дисперсия Var(y)?
Данные измерений переменной y в зависимости от переменной x приведены в таблице x = 1 2 5 3 7 4 6 8 y = 3 3 3 3 3 3 3 3 Предполагая линейную зависимость y от x: y=a+bx, построить регрессионное уравнение, т.е. найти коэффициенты a, b.
По некоторым данным о переменных x и y рассчитаны Var(x)=0.6, Var(y)=0.7, Cov(x,y)=0.4. Найти коэффициент корреляции r_xy между x и y.
По некоторым данным о переменных x и y рассчитаны x_ср=0.5, (x²)_ср=0.6, y_ср=0.7, (y²)_ср=1.2,(xy)_ср=0.75. Найти коэффициенты a и b регрессионного уравнения y=a+bx.
По таблице, содержащей 13 пар данных о переменных x и y, вычислены коэффициенты a=3.25, b=0.45, а также (x²_ср)=8.75 и r_xy=0.79. Найти 99% доверительные интервалы для a и b.
В каких из следующих выражений имеет место линейность по параметрам?

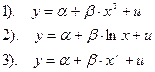
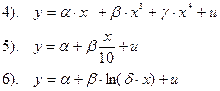
Вариант 7

Для переменных x 0.5 1.5 2.5 3.5 4.5 y 1.2 2.8 5.1 7.3 8.8 рассчитать выборочный коэффициент корреляции.
Показать, что если переменные x и y связаны линейным соотношением y=a+bx, то коэффициент корреляции между x и y ρ(x,y)=±1.
Зависимость переменной y от переменной x задана таблицей x = 1 2 5 3 7 4 6 8 y = 3 3 3 3 3 3 3 3 Показать, что Cov(x,y)=0.
Для переменных x и y, представленных ниже, рассчитать их средние величины, средние квадраты и средние произведения, а также коэффициент корреляции r_xy. x 0.5 1.5 2.5 3.5 4.5 y 1.2 2.8 5.1 7.3 8.8.
По таблице, содержащей 17 пар данных о переменных x и y, вычислены коэффициенты a=2.3, b=0.35, а также (x²_ср)=6.75 и r_xy=0.87. Найти 95% доверительные интервалы для a и b.
Какие из приведенных ниже уравнений допускают приведение к линейным регрессиям?

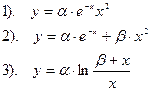
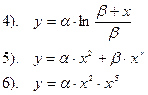
Вариант 8

Переменные x и y связаны соотношением y=a+bx. Дисперсия x равна Var(x). Чему равна ковариация между x и y?
Данные измерений переменной y в зависимости от переменной x приведены в таблице x = 1 2 5 3 7 4 6 8 y = 3 3 3 3 3 3 3 3 Предполагая линейную зависимость y от x: y=a+bx, построить регрессионное уравнение, т.е. найти коэффициенты a, b.
Показать, что если переменные x и y связаны линейным соотношением y=a+bx, то коэффициент корреляции между x и y ρ(x,y)=±1.
В некоторой таблице содержится информация о переменных y, x₁ и x₂. Предполагается построить линейную регрессионную модель 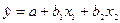. Расчеты дали значение для коэффициента корреляции между x₁ и x₂, равное 0.89. Следует ли придерживаться выбранной модели или выбрать иную?
По таблице, содержащей 13 пар данных о переменных x и y, вычислены коэффициенты a=3.25, b=0.45, а также (x²_ср)=8.75 и r_xy=0.79. Найти 99% доверительные интервалы для a и b.
Привести к линейному виду следующее выражение

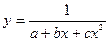
Вариант 9

Для переменных x 0.5 1.5 2.5 3.5 4.5 y 1.2 2.8 5.1 7.3 8.8 рассчитать выборочные дисперсии, выборочную ковариацию.
Дисперсия переменной x равна Var(x)=D². Переменная y линейно зависит от x: y=a+bx. Чему равна дисперсия y?
По некоторым данным о переменных x и y рассчитаны Var(x)=0.6, Var(y)=0.7, Cov(x,y)=0.4. Найти коэффициенты a и b регрессионного уравнения y=a+bx.
Дисперсия Var(x) является смещенной оценкой теоретической дисперсии σ²_x: E(Var(x))= 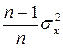.. Показать, что Var(x) является состоятельной оценкой для σ²_x.
По таблице, содержащей 17 пар данных о переменных x и y, вычислены коэффициенты a=2.3, b=0.35, а также (x²_ср)=6.75 и r_xy=0.87. Найти 95% доверительные интервалы для a и b.
В некоторой таблице содержится информация о переменных y, x₁ и x₂. Предполагается построить линейную регрессионную модель 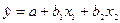. Расчеты дали значение для коэффициента корреляции между x₁ и x₂, равное 0.18. Следует ли придерживаться выбранной модели или выбрать иную?

Вариант 10

Переменные x и y связаны соотношением y=a+bx. Дисперсия x равна Var(x). Чему равна дисперсия Var(y)?
Для переменной x 0.5 1.5 2.5 3.5 4.5 рассчитать выборочную дисперсию.
По некоторым данным о переменных x и y рассчитаны Var(x)=0.6, Var(y)=0.7, Cov(x,y)=0.4. Найти коэффициент корреляции r_xy между x и y.
Дисперсия Var(x) является смещенной оценкой теоретической дисперсии σ²_x: E(Var(x))= 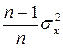. Показать, что Var(x) является состоятельной оценкой для σ²_x.

6. В каких из следующих выражений имеет место линейность по переменным?

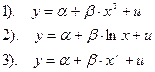
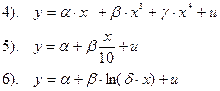
Вариант 11

Переменные x и y связаны соотношением y=a+bx. Дисперсия x равна Var(x). Чему равна ковариация между x и y?
Зависимость переменной y от переменной x задана таблицей x = 1 2 5 3 7 4 6 8 y = 3 3 3 3 3 3 3 3 Показать, что Cov(x,y)=0.
Для переменных x 0.5 1.5 2.5 3.5 4.5 y 1.2 2.8 5.1 7.3 8.8 рассчитать выборочный коэффициент корреляции.
По данным x 0.5 3.5 3.5 5.5 y 2.2 6.2 8.3 11.8 рассчитать коэффициенты a и b регрессионного уравнения y=a+bx.

6. Какие из приведенных ниже уравнений допускают приведение к линейным регрессиям?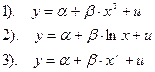

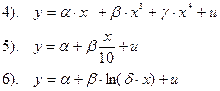
Вариант 12

1. Дисперсия переменной x равна Var(x)=D². Переменная y линейно зависит от x: y=a+bx. Чему равна дисперсия y?

2. Для переменных x 0.5 1.5 2.5 3.5 4.5 y 1.2 2.8 5.1 7.3 8.8 рассчитать выборочные дисперсии, выборочную ковариацию.

3. Показать, что если переменные x и y связаны линейным соотношением y=a+bx, то коэффициент корреляции между x и y ρ(x,y)=±1.

6. Какие из приведенных ниже уравнений допускают приведение к линейным регрессиям?

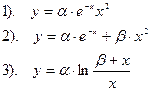
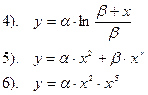
Вариант 13

Переменные x и y связаны соотношением y=a+bx. Дисперсия x равна Var(x). Чему равна ковариация между x и y?
Зависимость переменной y от переменной x задана таблицей x = 1 2 5 3 7 4 6 8 y = 3 3 3 3 3 3 3 3 Показать, что Cov(x,y)=0.
По некоторым данным о переменных x и y рассчитаны Var(x)=0.6, Var(y)=0.7, Cov(x,y)=0.4. Найти коэффициенты a и b регрессионного уравнения y=a+bx.
По некоторым данным о переменных x и y рассчитаны x_ср=0.5, (x²)_ср=0.6, y_ср=0.7, (y²)_ср=1.2,(xy)_ср=0.75. Найти коэффициент корреляции между x и y.
По таблице, содержащей 19 пар данных о переменных x и y, вычислены коэффициенты a=2.3, b=0.35, а также (x²_ср)=6.75 и r_xy=0.87. Найти 95% доверительные интервалы для a и b.
В каких из следующих выражений имеет место линейность по параметрам?

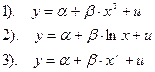
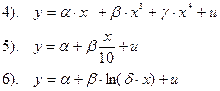
Вариант 14

Переменные x и y связаны соотношением y=a+bx. Дисперсия x равна Var(x). Чему равна дисперсия Var(y)?
Данные измерений переменной y в зависимости от переменной x приведены в таблице x = 1 2 5 3 7 4 6 8 y = 3 3 3 3 3 3 3 3 Предполагая линейную зависимость y от x: y=a+bx, построить регрессионное уравнение, т.е. найти коэффициенты a, b.
По некоторым данным о переменных x и y рассчитаны Var(x)=0.6, Var(y)=0.7, Cov(x,y)=0.4. Найти коэффициент корреляции r_xy между x и y.
По некоторым данным о переменных x и y рассчитаны x_ср=0.5, (x²)_ср=0.6, y_ср=0.7, (y²)_ср=1.2,(xy)_ср=0.75. Найти коэффициенты a и b регрессионного уравнения y=a+bx.
По таблице, содержащей 15 пар данных о переменных x и y, вычислены коэффициенты a=3.25, b=0.45, а также (x²_ср)=8.75 и r_xy=0.79. Найти 99% доверительные интервалы для a и b.
В каких из следующих выражений имеет место линейность по переменным?

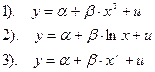
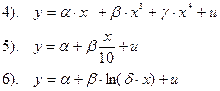
Вариант 15

Дисперсия переменной x равна Var(x)=D². Переменная y линейно зависит от x: y=a+bx. Чему равна дисперсия y?
Показать, что если переменные x и y связаны линейным соотношением y=a+bx, то коэффициент корреляции между x и y ρ(x,y)=±1.
Для переменной x = 0.5 1.5 2.5 3.5 4.5 рассчитать выборочную дисперсию.
Для переменных x и y, представленных ниже, рассчитать их средние величины, средние квадраты и средние произведения, а также коэффициент корреляции r_xy. x 0.5 1.5 2.5 3.5 4.5 y 1.2 2.8 5.1 7.3 8.8.
По таблице, содержащей 13 пар данных о переменных x и y, вычислены коэффициенты a=2.3, b=0.35, а также (x²_ср)=6.75 и r_xy=0.87. Найти 95% доверительные интервалы для a и b.
Какие из приведенных ниже уравнений допускают приведение к линейным регрессиям?

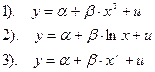
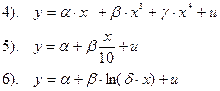
Вариант 16

Переменные x и y связаны соотношением y=a+bx. Дисперсия x равна Var(x). Чему равна дисперсия Var(y)?
Для переменных x 0.5 1.5 2.5 3.5 4.5 y 1.2 2.8 5.1 7.3 8.8 рассчитать выборочные дисперсии, выборочную ковариацию.
По некоторым данным о переменных x и y рассчитаны Var(x)=0.6, Var(y)=0.7, Cov(x,y)=0.4. Найти коэффициенты a и b регрессионного уравнения y=a+bx.
В некоторой таблице содержится информация о переменных y, x₁ и x₂. Предполагается построить линейную регрессионную модель 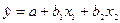. Расчеты дали значение для коэффициента корреляции между x₁ и x₂, равное 0.89. Следует ли придерживаться выбранной модели или выбрать иную?
По таблице, содержащей 17 пар данных о переменных x и y, вычислены коэффициенты a=3.25, b=0.45, а также (x²_ср)=8.75 и r_xy=0.79. Найти 99% доверительные интервалы для a и b.
Какие из приведенных ниже уравнений допускают приведение к линейным регрессиям?

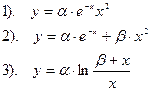
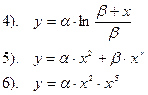
Вариант 17

Для переменных x 0.5 1.5 2.5 3.5 4.5 y 1.2 2.8 5.1 7.3 8.8 рассчитать выборочный коэффициент корреляции.
Дисперсия переменной x равна Var(x)=D². Переменная y линейно зависит от x: y=a+bx. Чему равна дисперсия y?
Данные измерений переменной y в зависимости от переменной x приведены в таблице x = 1 2 5 3 7 4 6 8 y = 3 3 3 3 3 3 3 3 Предполагая линейную зависимость y от x: y=a+bx, построить регрессионное уравнение, т.е. найти коэффициенты a, b.
По некоторым данным о переменных x и y рассчитаны x_ср=0.5, (x²)_ср=0.6, y_ср=0.7, (y²)_ср=1.2,(xy)_ср=0.75. Найти коэффициент корреляции между x и y.
По таблице, содержащей 21 пару данных о переменных x и y, вычислены коэффициенты a=2.3, b=0.35, а также (x²_ср)=6.75 и r_xy=0.87. Найти 95% доверительные интервалы для a и b.
Какие из приведенных ниже уравнений допускают приведение к линейным регрессиям?

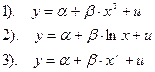
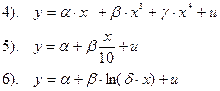
Вариант 18

Переменные x и y связаны соотношением y=a+bx. Дисперсия x равна Var(x). Чему равна дисперсия Var(y)?
Данные измерений переменной y в зависимости от переменной x приведены в таблице x = 1 2 5 3 7 4 6 8 y = 3 3 3 3 3 3 3 3 Предполагая линейную зависимость y от x: y=a+bx, построить регрессионное уравнение, т.е. найти коэффициенты a, b.
По некоторым данным о переменных x и y рассчитаны Var(x)=0.6, Var(y)=0.7, Cov(x,y)=0.4. Найти коэффициент корреляции r_xy между x и y.
По некоторым данным о переменных x и y рассчитаны x_ср=0.5, (x²)_ср=0.6, y_ср=0.7, (y²)_ср=1.2,(xy)_ср=0.75. Найти коэффициенты a и b регрессионного уравнения y=a+bx.
По таблице, содержащей 23 пар данных о переменных x и y, вычислены коэффициенты a=3.25, b=0.45, а также (x²_ср)=8.75 и r_xy=0.79. Найти 99% доверительные интервалы для a и b.
В каких из следующих выражений имеет место линейность по параметрам?

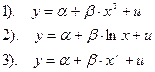
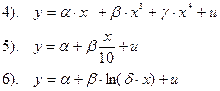
Вариант 19

Для переменных x 0.5 1.5 2.5 3.5 4.5 y 1.2 2.8 5.1 7.3 8.8 рассчитать выборочный коэффициент корреляции.
Показать, что если переменные x и y связаны линейным соотношением y=a+bx, то коэффициент корреляции между x и y ρ(x,y)=±1.
Зависимость переменной y от переменной x задана таблицей x = 1 2 5 3 7 4 6 8 y = 3 3 3 3 3 3 3 3 Показать, что Cov(x,y)=0.
Для переменных x и y, представленных ниже, рассчитать их средние величины, средние квадраты и средние произведения, а также коэффициент корреляции r_xy. x 0.5 1.5 2.5 3.5 4.5 y 1.2 2.8 5.1 7.3 8.8.
По таблице, содержащей 27 пар данных о переменных x и y, вычислены коэффициенты a=2.3, b=0.35, а также (x²_ср)=6.75 и r_xy=0.87. Найти 95% доверительные интервалы для a и b.
Какие из приведенных ниже уравнений допускают приведение к линейным регрессиям?

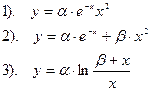
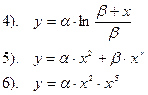
Вариант 20

Переменные x и y связаны соотношением y=a+bx. Дисперсия x равна Var(x). Чему равна ковариация между x и y?
Данные измерений переменной y в зависимости от переменной x приведены в таблице x = 1 2 5 3 7 4 6 8 y = 3 3 3 3 3 3 3 3 Предполагая линейную зависимость y от x: y=a+bx, построить регрессионное уравнение, т.е. найти коэффициенты a, b.
Показать, что если переменные x и y связаны линейным соотношением y=a+bx, то коэффициент корреляции между x и y ρ(x,y)=±1.
В некоторой таблице содержится информация о переменных y, x₁ и x₂. Предполагается построить линейную регрессионную модель 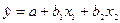. Расчеты дали значение для коэффициента корреляции между x₁ и x₂, равное 0.89. Следует ли придерживаться выбранной модели или выбрать иную?
По таблице, содержащей 23 пары данных о переменных x и y, вычислены коэффициенты a=3.25, b=0.45, а также (x²_ср)=8.75 и r_xy=0.79. Найти 99% доверительные интервалы для a и b.
Привести к линейному виду следующее выражение

<6 7 8910 11 12 >

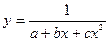
Дата добавления: 2014-12-07; просмотров: 1111;