Решение. Расстояние от точки до плоскости представляет собой длину перпендикуляра, опущенного из точки на плоскость
Расстояние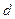 
от точки 
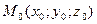до плоскости 
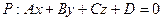представляет собой длину перпендикуляра, опущенного из точки на плоскость, и определяется формулой
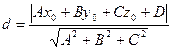(3.10)
Для плоскости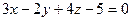 
координаты нормального вектора 
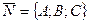определяются равенствами 
, 
, 
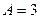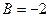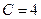. Следовательно, 
.
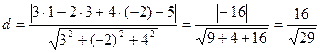6) Составить канонические уравнения прямой, проходящей через точки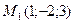 
и 
.
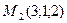Дата добавления: 2014-12-07; просмотров: 799;