Случай первый. Самый лёгкий. Если степень – целое число.

Например:

Представим интеграл в стандартном виде (это лучше делать на черновике):

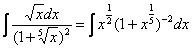
Мы видим, что степень – целая, а, значит, действительно имеет место первый случай. На самом деле биномиальный интеграл первого типа решается практически так же, как интегралы в примерах 5, 6, поэтому приводить почти такие же решения особого смысла нет – я просто покажу, какую замену здесь нужно провести.
Смотрим на знаменатели дробей:

Записываем знаменатели: 2, 5. Находим наименьшее общее кратное этих чисел. Очевидно, это 10: оно делится и на 2 и на 5, кроме того – десятка самая маленькая в этом смысле.
После замены все корни гарантировано пропадут. Повторюсь, примеров для первого случая не будет, так как они очень похожи на недавно разобранные интегралы.