Указания к выполнению работы. Под статистической гипотезой понимается суждение, сделанное относительно свойств статистической совокупности на основе выборки
Под статистической гипотезой понимается суждение, сделанное относительно свойств статистической совокупности на основе выборки. Проверка статистической гипотезы – это процедура, по результатам которой гипотеза принимается или отвергается.
Особое место среди статистических гипотез занимает нулевая гипотеза. Ее следует понимать как предположение о том, что параметры выборочных совокупностей являются оценками соответствующих параметров генеральной совокупности или выборочные совокупности являются представителями одной генеральной совокупности.
Проверка статистических гипотез состоит в решении вопроса, будет ли гипотеза принята или ее надлежит отвергнуть. Мерой отличия параметров совокупностей служит их разность (различие) или отношение. Для многих случаев вероятности отклонения сравниваемых параметров случайных величин вычислены и сведены в таблицы. Пользуясь ими по определенным правилам, можно провести проверку гипотезы. При проверке гипотезы возможны ошибки двух родов.
Ошибка первого рода состоит в том, что нулевая гипотеза отвергается, когда она на самом деле верна. Ошибка второго рода состоит в том, что нулевая гипотеза принимается, хотя она и не верна. Вероятность допустить ошибку первого рода, выраженную в процентах, называется уровнем значимости q. Это означает, что с вероятностью P=1-q гипотеза действительно верна. Вероятность увеличивается, если уменьшить уровень значимости. Обычно в технологических расчетах берут q£5%.
3.2.1 Методика проверки однородности дисперсий
1. Заполняем табл. 3.4 по образцу табл. 3.1 данными значений К, приведенными в табл. 2.3 лабораторной работы № 2 (значения К размещены в прямоугольнике таблицы).
Таблица 3.4
Результаты имитационного эксперимента
 № серии № серии
| Значения x для ℓ-го дублированного опыта, yJl | yJ | SJ2 | ||||||||||
| J | e | ||||||||||||
| 0,01 | 37,6 | 38,8 | 41,0 | 38,0 | 35,3 | 34,6 | 34,6 | 34,6 | 35,4 | 38,0 | 36,8 | 4,94 | |
| 0,02 | 44,1 | 38,0 | 31,2 | 34,2 | 31,2 | 38,0 | 31,2 | 37,2 | 37,2 | 32,7 | 35,5 | 17,48 | |
| 0,01 | 38,8 | 38,0 | 40,3 | 36,7 | 40,3 | 37,6 | 38,0 | 39,5 | 38,0 | 38,8 | 38,6 | 1,06 | |
| 0,02 | 37,2 | 34,2 | 31,2 | 34,2 | 35,7 | 35,7 | 41,0 | 32,7 | 42,1 | 41,0 | 36,5 | 14,70 | |
| 0,01 | 41,0 | 41,0 | 40,3 | 34,6 | 40,3 | 34,6 | 39,5 | 36,7 | 34,6 | 40,6 | 38,1 | 11,60 |

 В табл. 3.4 приведены результаты имитационного эксперимента, включающего 5 серий опытов (J=1m). Каждая серия содержит 10 дублированных опытов (ℓ=1n). Общее количество опытов mn=5×10=50.
В табл. 3.4 приведены результаты имитационного эксперимента, включающего 5 серий опытов (J=1m). Каждая серия содержит 10 дублированных опытов (ℓ=1n). Общее количество опытов mn=5×10=50.
2. Определение выборочного среднего 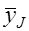 и дисперсий
и дисперсий 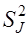 . Выборочное среднее для каждой серии J определяется по формуле (2.8) (лабораторной работы № 2), а дисперсия по формуле (2.9): например,
. Выборочное среднее для каждой серии J определяется по формуле (2.8) (лабораторной работы № 2), а дисперсия по формуле (2.9): например,
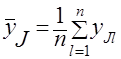 ,
, 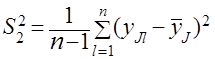
и аналогично для других серий опытов.
 Расчетные значения y и S2 для рассматриваемого практического примера приведены в табл. (3.4).
Расчетные значения y и S2 для рассматриваемого практического примера приведены в табл. (3.4).
3. Проверка однородности нескольких дисперсий S12,...., Sn2 при равных объемах выборок (n1=.....=nJ=n=10). Определяют расчетное значение G-критерия Кохрана:
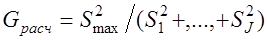 . (3.1)
. (3.1)
Далее по уровню значимости q, числу степеней свободы f=n-1 и по числу выборок m из таблицы распределения Кохрана определяют величину Gтабл.
Если Gрасч.< Gтабл, то принимают гипотезу об однородности дисперсий. В противном случае гипотеза отвергается.
Для практического примера, данные которого приведены в табл.(3.4), получим: Gрасч по формуле (3.1)
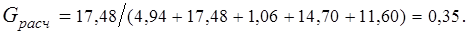
Табличное значение критерия Кохрана Gтабл для принятых значений: q=5%, f=10-1=9 и m=5 равно 0,42.
Имеем Gрасч.< Gтабл., следовательно, дисперсии выборок однородны или выборки являются представителями одной генеральной совокупности.
4. Проверка однородности двух дисперсий. Для проверки статистической гипотезы об однородности двух дисперсий используют F-критерий Фишера. Пусть S12>S22, тогда расчетное значение F-критерия Фишера, Fрасч. определится по формуле [4]
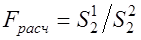 . (3.2)
. (3.2)
Задаемся уровнем значимости (обычно при исследованиях процессов деревообработки q=0,05), вычисляем число степеней свобод f1=n1-1, f2=n2-1. По величинам q, f1 и q, f2 из табл. П.6 Приложения отыскивают табличное значение критерия Fтабл.
Если Fрасч>Fтабл, то выборочные дисперсии неоднородны. Если Fрасч£Fтабл, то гипотеза об однородности дисперсий принимается.
Проверим однородность дисперсии 4-й и 5-й серий опытов нашего примера (табл. 3.4): S24=14,70; S25=11,6; S24>S25; n4=n5=n=10; f4=f5=f=10-1=9. Примем уровень значимости q=5%. Расчетное значение Fрасч. критерия Фишера определяется по формуле 3.2
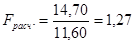 .
.
Табличное значение Критерия по табл. П.6, Fтабл. =3,23, Fрасч.£Fтабл. Гипотеза об однородности дисперсий S24 и S25 принимается.
3.2.2 Методика проверки гипотезы об однородности средних
двух выборок
Данная проверка позволяет установить, вызвано ли расхождение средних двух выборок случайными ошибками или оно связанно с влиянием неслучайных факторов. Для проверки однородности средних y1 и y2 необходимо дополнительно знать объемы выборок n1 и n2 и дисперсии S21 и S22.

 При этом возможны два варианта: дисперсии S21 и S22 однородны или неоднородны.
При этом возможны два варианта: дисперсии S21 и S22 однородны или неоднородны.
Вариант 1 - дисперсии S21 и S22 однородны. Определяется расчетное значение t-критерия Стьюдента по формуле [4], когда n1¹n2
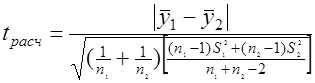 , (3.3)
, (3.3)
при n1=n2=n
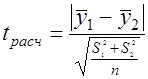 . (3.4)
. (3.4)

 Из таблиц распределения Стьюдента по уровню значимости и числу степеней свободы f= n1+n2-2 отыскивают табличное значение tтабл. Если tрасч>tтабл, то расхождение между средними значимо. В противном случае, если tрасч<tтабл, то принимают гипотезу об однородности средних. Выполним проверку однородности средних 4-й и 5-й серии опытов нашего примера (табл. 3.4) y4=36,5 и y5=38,1. Дисперсии этих серий S24=14,7 и S25=11,6 однородны, что установлено выше (П.4).
Из таблиц распределения Стьюдента по уровню значимости и числу степеней свободы f= n1+n2-2 отыскивают табличное значение tтабл. Если tрасч>tтабл, то расхождение между средними значимо. В противном случае, если tрасч<tтабл, то принимают гипотезу об однородности средних. Выполним проверку однородности средних 4-й и 5-й серии опытов нашего примера (табл. 3.4) y4=36,5 и y5=38,1. Дисперсии этих серий S24=14,7 и S25=11,6 однородны, что установлено выше (П.4).
Определяем расчетное значение t-критерия Стьюдента по формуле (3.4), так как n4=n5=n=10
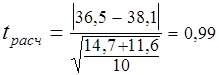 .
.
Для числа степеней свободы f= n1+n2-2=18 и принятом 5%-ном уровне значимости q=5% по табл. П.3 отыскиваем табличное значение, tтабл =2,1. Поскольку tрасч<tтабл , гипотеза об однородности средних принимается.
Вариант 2. Дисперсии 2-й и 3-й серий опытов нашего примера (табл. 3.4) S22=17,48 и S23=1,06 неоднородны. Проверке однородности средних двух выборок должна предшествовать проверка однородности их дисперсий.
По формуле (3.2) определяем расчетное значение F-критерия Фишера
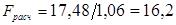
Для степеней свободы f1=f2=f=10-1=9 табличное значение F-критерия Фишера при уровне значимости q=5% по табл. П.6: равно Fтабл=3,23. Гипотеза об однородности дисперсий S22 и S23 при Fрасч>Fтабл отвергается.

 Для двух выборок с неоднородными дисперсиями процедура проверки однородности средних y2=35,5 и y3=38,6 выполняется в следующем порядке.
Для двух выборок с неоднородными дисперсиями процедура проверки однородности средних y2=35,5 и y3=38,6 выполняется в следующем порядке.
Определяется расчетное значение t-критерия Стьюдента по формуле [4]
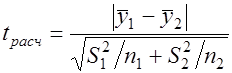 , (3.5)
, (3.5)
а число степеней свободы f по формуле
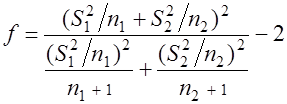 . (3.6)
. (3.6)
Найденное значение числа степеней свободы f округляют до целого. По этому числу степенной свободы и уровню значимости q по таблице распределения Стьюдента определяют tтабл. Если tрасч>tтабл, то расхождение между средними значимо. В противном случае принимают гипотезу об однородности средних.
Определим расчетное значение t-критерия Стьюдента для рассматриваемого примера по формуле (3.5)
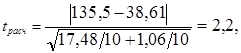
а число степеней свободы f определяем по формуле (3.6)
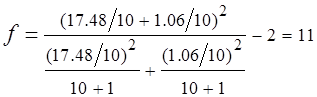 .
.

 По табл. П.3 Приложения для f=11 и принятом q=5% находим табличное значение t-критерия Стьюдента, tтабл=2,2. Поскольку tрасч. не превышает табличное tтабл., значение критерия гипотеза об однородности средних y2 и y3 принимается.
По табл. П.3 Приложения для f=11 и принятом q=5% находим табличное значение t-критерия Стьюдента, tтабл=2,2. Поскольку tрасч. не превышает табличное tтабл., значение критерия гипотеза об однородности средних y2 и y3 принимается.
Если средние однородны в случае неоднородности дисперсий, то следует выбирать тот технологический процесс, при котором получается продукция с меньшей дисперсией.
3.2.3 Методика проверки гипотезы о нормальности
распределения случайных величин
3.2.3.1 Общие сведения
Часто необходимо знать закон распределения генеральной совокупности. Если имеются основания предположить, что это определенный закон, выдвигают гипотезу, что генеральная совокупность распределяется по данному закону. Большинство статистических оценок предполагает нормальное распределение результатов опытов. Для проверки гипотезы о виде распределения используют критерии согласия.
Сущность проверки по критерию согласия состоит в том, что выборка сравнивается с некоторым заранее намеченным теоретическим распределением. Вид теоретического распределения выбирается по характеру кривой эмпирического распределения. В большинстве случаев задаются нормальные теоретические распределения. При проверке гипотезы о виде закона распределения, как правило, используют критерий c2 (хи-квадрат)
К. Пирсона. При его помощи можно сравнивать эмпирическое и теоретическое распределения или два различных эмпирических распределения.
Для проверки гипотезы о нормальности эмпирического распределения по критерию c2 находится сумма отношений квадратов разностей между частотами эмпирического и теоретического распределения к теоретическим частотам
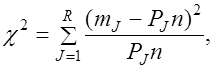 (3.7)
(3.7)
где R – количество интервалов, на которые разбиты опытные данные;
PJ – теоретические вероятности попадания опытных данных в J-й интервал;
PJn – теоретические частоты попаданий опытных данных в J-й интервал (с округлением до ближайшего целого числа);
mJ – эмпирические частоты попадания случайной величины в J-й интервал.
Вычисление теоретических вероятностей PJ производится по формуле [4]
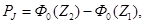 (3.8)
(3.8)
где Ф0(Z) – нормированная функция Лапласа, определяется по табл. П.7 Приложения.
Аргументы Z2 и Z1 функции Лапласа определяются из выражений
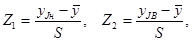 (3.9)
(3.9)
где yJН и yJB – соответственно нижняя и верхняя границы интервала.
Для отрицательного значения аргумента функция Лапласа также отрицательна.
Просуммировав значения c2 по формуле (3.7), получим расчетное значение критерия Пирсона c2расч. Для определения c2табл рассчитывается число степеней свободы по формуле
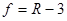 (3.10)
(3.10)
и задается уровень значимости q. По табл. П.7 Приложения находится значение c2табл. Если c2расч£c2табл гипотеза о нормальности распределения принимается. Если c2расч.>c2табл. , то нулевая гипотеза отвергается.
Предварительно, до проверки нормальности распределения по c2 Пирсона, проводится приближенная проверка его нормальности при помощи показателей асимметрии А и эксцесса Е, расчитываемых по формулам [4]
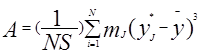 , (3.11)
, (3.11) 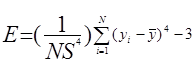 , (3.12)
, (3.12)
где S – эмпирический стандарт выборки (среднее квадратическое отклонение);
N – объем выборки ( 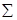 mJ);
mJ);
 y – среднее значение выборки объемом N.
y – среднее значение выборки объемом N.
Затем вычисляют средние квадратические отклонения для асимметрии sА и эксцесса sЕ по формулам [4]
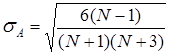 , (3.13)
, (3.13)
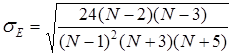 . (3.14)
. (3.14)
Если хотя бы одно значение из показателей А или Е по абсолютной величине в 2…3 раза превосходит значение соответствующего квадратического отклонения, то следует усомниться в нормальности распределения случайной величины и провести проверку с помощью c2-критерия Пирсона.
3.2.3.2 Пример проверки гипотезы о нормальности распределения
1. Проверку нормальности распределения случайных величин выполним для выборки сформированной в лабораторной работе № 2 (табл. 2.4). Для расчета показателей асимметрии, эксцесса и c2-критерия используются результаты расчетов статистических выборок по табл. (2.4) и (2.5). Это границы интервалов yJН и yJB, число наблюдений в интервале mJ, относительную частоту PJ*, разность средних в интервале и выборке (yJ*-y).

 2. Предварительная проверка нормальности распределения. Дополним табл. 3.2 необходимыми для расчета асимметрии и эксцесса данными из табл. 2.4 и представим ее в виде табл. 3.5
2. Предварительная проверка нормальности распределения. Дополним табл. 3.2 необходимыми для расчета асимметрии и эксцесса данными из табл. 2.4 и представим ее в виде табл. 3.5
Таблица 3.5
Выборочные показатели асимметрии и эксцесса
      Номер
интервала,
J Номер
интервала,
J
| Число наблюдений в интервале, mJ | Середина интервала, yJ* | Среднее выборки, y | yJ*-y | (yJ*-y)3 | mJ(yJ*-y)3 | (yJ*-y)4 | mJ(yJ*-y)4 |
| 31,65 | 37,0 | -6,65 | 294,0 | 1176,0 | 1955,0 | 7820,0 | ||
| 33,65 | 37,0 | -4,65 | 100,4 | 467,0 | ||||
| 35,65 | 37,0 | -2,65 | 18,6 | 111,6 | 49,3 | 295,8 | ||
| 37,65 | 37,0 | 0,65 | 0,3 | 4,2 | 0,2 | 2,8 | ||
| 39,65 | 37,0 | 2,65 | 18,6 | 148,8 | 49,3 | 394,4 | ||
| 41,65 | 37,0 | 4,65 | 100,4 | 602,4 | 467,0 | |||
| 43,65 | 37,0 | 6,65 | 294,0 | 294,0 | 1955,0 |
å 3438 å 18406,6
Рассчитаем показатели нормальности распределения для выборки с объемом N=50 и эмпирическим стандартом S=3.75 (см. табл. 2.5). Показатель асимметрии А по формуле 3.11 равен
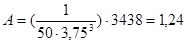 ,
,
показатель эксцесса Е по формуле (3.12) равен
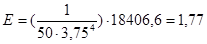 ,
,
среднее квадратическое отклонение асимметрии sА по формуле (3.14) равно
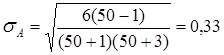 .
.
среднее квадратическое отклонение эксцесса sЕ по формуле (3.14) равно
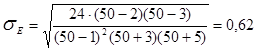 .
.
Полученные показатели А=1,03 и sА=0,33, Е=1,48 и sЕ=0,62 и их отклонения А/sА=3,1 и Е/sЕ=2,4 хотя и удовлетворяют требованиям нормальности распределения, но находятся вблизи критической области. В связи с этим целесообразно выполнить проверку нормальности распределения по критерию c2 Пирсона.
3. Проверка нормальности распределения по критерию c2 Пирсона. Для определения расчетного значения c2- критерия Пирсона по формуле (3.7) составляется вспомогательная табл. 3.6 по форме табл. 3.3.
Таблица 3.6
Результаты вычисления значений c2- критерия Пирсона
| № интервала | yJH | yJB | mJ | Z1 | Z2 | Ф( Z1) | Ф( Z2) | РJ | РJn | (mJ- РJn) | (mJ- РJn)2 | (mJ- РJn)2 РJn |
 1 1
| 30,65 | 32,65 | -1,69 | -1,16 | -0,4454 | -0,3749 | 0,070 | 3,5 | 0,5 | 0,25 | 0,07 | |
 2 2
| 32,65 | 34,65 | -1,16 | -0,63 | -0,39794 | -0,2353 | 0,140 | 7,0 | 4,0 | 16,0 | 2,28 | |
 3 3
| 34,65 | 36,65 | -0,63 | -0,09 | -0,2353 | -0,0353 | 0,200 | 10,0 | 4,0 | 16,0 | 1,60 | |
 4 4
| 36,65 | 38,65 | -0,09 | 0,44 | -0,0953 | 0,1700 | 0,205 | 10,2 | 3,8 | 14,4 | 1,41 | |
 5 5
| 38,65 | 40,65 | 0,44 | 0,97 | 0,1700 | 0,3337 | 0,164 | 8,2 | 0,2 | 0,04 | 0,005 | |
 6 6
| 40,65 | 42,65 | 0,97 | 1,51 | 0,3337 | 0,4332 | 0,600 | 5,0 | 0,20 | |||
 7 7
| 42,65 | 44,65 | 1,51 | 2,04 | 0,4332 | 0,4782 | 0,045 | 2,25 | 1,25 | 1,56 | 1,25 |
Σ=6,82
Расчетное значение c2- критерия Пирсона c2=6,82. Табличное значение c2табл для числа степеней свободы f=R-3=7-3=4 и принятом 5%-ном уровне значимости q по табл. П.8 Приложения составит c2табл=9,49. В нашем примере c2расч<c2табл, следовательно, нулевая гипотеза о нормальности распределения случайных величин (К - удельной работы резания) принимается.
4. Построение нормальной кривой по опытным данным [7, §7 гл.17]. Теоретическая кривая нормального распределения по данным наблюдений рассчитывается следующим образом:
 а) устанавливаются значения выборочного среднего и эмпирического стандарта: y=37; S=3,75 для нашей кривой;
а) устанавливаются значения выборочного среднего и эмпирического стандарта: y=37; S=3,75 для нашей кривой;
б) рассчитываются ординаты nJ (выравнивающие частоты) теоретической кривой по формуле
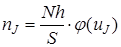 , (3.15)
, (3.15)
где N – число испытаний (опытов);
h – длина интервала, h=2 для нашего случая;
φ(uJ) –дифференциальная функция нормированного распределения (нормальная плотность ряда)
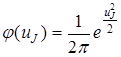 . (3.16)
. (3.16)
Аргумент из функции j (uJ) определяют из выражения
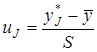 . (3.17)
. (3.17)
где yJ* - середина J-го интервала (табл. 3.5).
 В приближении при (yJ*-y)®0 наибольшая ордината кривой (частота) составит
В приближении при (yJ*-y)®0 наибольшая ордината кривой (частота) составит
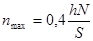 . (3.18)
. (3.18)
 Некоторые значения j (u) при малых величинах разности (y-y) приведены в таблице 3.7.
Некоторые значения j (u) при малых величинах разности (y-y) приведены в таблице 3.7.
Таблица 3.7
Значения функции j (u)
| u | 0,1 | 0,2 | 0,3 | 0,5 | 1,0 | |
| j (u) | 0,3983 | 0,3970 | 0,3910 | 0,3914 | 0,3521 | 0,2420 |
 Определим максимальную ординату кривой для минимальной разности (yJ*-y)=0,65 (табл.3.5). По формуле (3.17) имеем
Определим максимальную ординату кривой для минимальной разности (yJ*-y)=0,65 (табл.3.5). По формуле (3.17) имеем
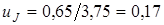 .
.
По табл. 3.7 определим значение функции j (uJ)=0,3952, а по формуле (3.15) частоту nmax
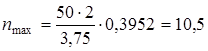 .
.
Округляем величину максимальной частоты теоретической кривой распределения, nmax=11.
в) каждая из ветвей симметричной кривой нормального распределения строится не менее, чем по четырем точкам. Ординаты остальных точек кривой строят в соответствии с абсциссами, выраженными в долях S, приведенными табл. 3.8.
Таблица 3.8
Значение ординат теоретической кривой распределения
| Доля S | ±0,5 S | ±1,0 S | ±1,5 S | ±2,0 S | ±2,5 S | ±3,0 S | |
| КJ=nJ/nmax | 0,883 | 0,607 | 0,325 | 0,135 | 0,044 | 0,011 |
По приведенным данным вычисляются значения других ординат кривой (табл.3.9)

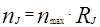 (3.19)
(3.19)
Расчеты выравнивающих частот nJ и функции плотности вероятности для нашего примера приведены в табл. 3.9.
Таблица 3.9
Значения кривой нормального распределения
| Доля S | 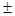 0,5S 0,5S
| 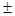 1S 1S
| 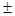 1,5S 1,5S
| 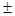 2,0S 2,0S
| 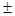 2,5S 2,5S
| 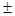 3,0S 3,0S
| |
| yJ | 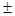 1,8 1,8
| 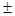 3,7 3,7
| 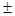 5,6 5,6
| 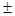 7,5 7,5
| 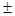 9,4 9,4
| 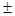 11,3 11,3
| |
| КJ=nJ/nmax | 0,883 | 0,607 | 0,325 | 0,135 | 0,044 | 0,011 | |
| nJ= КJ nmax | |||||||
Р 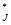 =nJ/N (f(y)) =nJ/N (f(y))
| 0,22 | 0,20 | 0,16 | 0,084 | 0,040 | 0,005 | |
 у, мм у, мм
|
По результатам вычислений строятся совмещенные графики опытных данных (гистограммы) и нормальной кривой, приведенных на рис. 3.1.
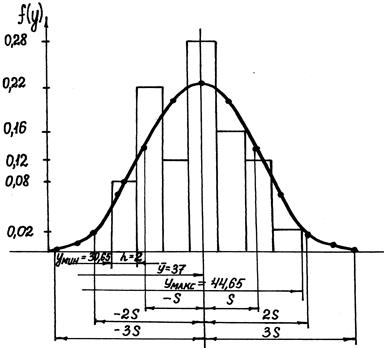 |
Рис. 3.1. Кривая нормального распределения,
совмещенная с гистограммой выборки
Большинство статистических оценок предполагает нормальное распределение результатов опытов и может быть несправедливо в случае другого распределения. Поэтому применение этих оценок допустимо лишь при достаточной уверенности, что распределение этих величин близко к нормальному.
Лабораторная работа № 4
Дата добавления: 2014-12-05; просмотров: 1025;
