Производная функции в точке

Как найти производную функции в точке? Из формулировки следуют два очевидных пункта этого задания:

1) Необходимо найти производную.

2) Необходимо вычислить значение производной в заданной точке.

Пример 1

Вычислить производную функции 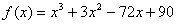в точке

Справка:Следующие способы обозначения функции эквивалентны:


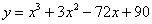
В некоторых задания бывает удобно обозначить функцию «игреком», а в некоторых через «эф от икс».

Сначала находим производную:

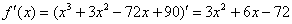
Надеюсь, многие уже приноровились находить такие производные устно.

На втором шаге вычислим значение производной в точке :

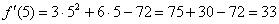
Готово.

Небольшой разминочный пример для самостоятельного решения:

Пример 2

Вычислить производную функции 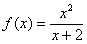в точке

Полное решение и ответ в конце урока.

Необходимость находить производную в точке возникает в следующих задачах: построение касательной к графику функции, исследование функции на экстремум, исследование функции на перегиб графика, полное исследование функции и др. Со временем, надеюсь, я обо всём расскажу.

Но рассматриваемое задание встречается в контрольных работах и само по себе. И, как правило, в таких случаях функцию дают достаточно сложную. В этой связи рассмотрим еще два примера.

Пример 3

Вычислить производную функции 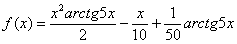в точке .
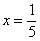Сначала найдем производную:

Производная, в принципе, найдена, и можно подставлять требуемое значение 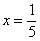. Но что-то делать это не сильно хочется. Выражение очень длинное, да и значение «икс» у нас дробное. Поэтому стараемся максимально упростить нашу производную. В данном случае попробуем привести к общему знаменателю три последних слагаемых:

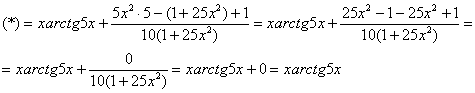
Ну вот, совсем другое дело. Вычислим значение производной в точке :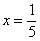

В том случае, если Вам не понятно, как найдена производная, вернитесь к первым двум урокам темы. Если возникли трудности (недопонимание) с арктангенсом и его значениями, обязательно изучите методический материал Графики и свойства элементарных функций – самый последний параграф. Потому-что арктангенсов на студенческий век ещё хватит.

Пример 4

Вычислить производную функции в точке .

Это пример для самостоятельного решения.