Производная произведения функций

Вроде бы по аналогии напрашивается формула …., но неожиданность состоит в том, что:

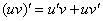
Я не буду объяснять, почему именно так, наша задача научиться решать производные, а не разбираться в теории.

Пример 5

Найти производную функции

Здесь у нас произведение двух функций, зависящих от .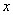
Сначала применяем наше странное правило, а затем превращаем функции по таблице производных:

Сложно? Вовсе нет, вполне доступно даже для чайника.

Пример 6

Найти производную функции

В данной функции содержится сумма и произведение двух функций – квадратного трехчлена и логарифма . Со школы мы помним, что умножение и деление имеют приоритет перед сложением и вычитанием.

Здесь всё так же. СНАЧАЛА мы используем правило дифференцирования произведения:

Теперь для скобки используем два первых правила:

В результате применения правил дифференцирования под штрихами у нас остались только элементарные функции, по таблице производных превращаем их в другие функции:

Готово.

При определенном опыте нахождения производных, простые производные вроде не обязательно расписывать так подробно. Вообще, они обычно решаются устно, и сразу записывается, что .

Пример 7

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока)