Транспортная задача линейного программирования
Задача 6. На двух складах хранится однородный товар в объёмах 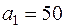 ,
, 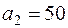 . Его необходимо доставить в четыре магазина, потребности которых b1=30, b2=30, b3=20, b4=20. Удельные транспортные затраты на перевозки:
. Его необходимо доставить в четыре магазина, потребности которых b1=30, b2=30, b3=20, b4=20. Удельные транспортные затраты на перевозки: 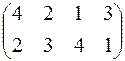 . Для данной задачи составить оптимальный план перевозок.
. Для данной задачи составить оптимальный план перевозок.
Определим тип задачи:
 - суммарные запасы;
- суммарные запасы;
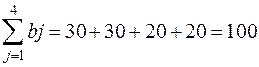 - суммарные потребности.
- суммарные потребности.
Т.к. 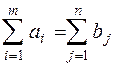 , то задача закрытая.
, то задача закрытая.
Если выполняется неравенство 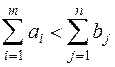 - транспортная задача называется открытой транспортной задачей с избыточным спросом. Она может быть приведена к закрытой задаче, если ввести в рассмотрение условного поставщика
- транспортная задача называется открытой транспортной задачей с избыточным спросом. Она может быть приведена к закрытой задаче, если ввести в рассмотрение условного поставщика 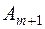 , величина запасов у которого:
, величина запасов у которого: 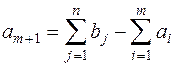 , а удельные транспортные затраты по перевозке груза от условного поставщика ко всем потребителям принимаются равными 0:
, а удельные транспортные затраты по перевозке груза от условного поставщика ко всем потребителям принимаются равными 0: 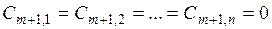 . Компоненты
. Компоненты 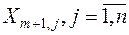 найденного плана поставок означают количество товара, которое недополучит потребитель
найденного плана поставок означают количество товара, которое недополучит потребитель 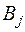 .При этом матрица планирования транспортной задачи дополняется одной строкой.
.При этом матрица планирования транспортной задачи дополняется одной строкой.
Если выполняется неравенство 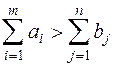 - транспортная задача называется открытой транспортной задачей с избыточным предложением. Она может быть приведена к закрытой задаче, если ввести в рассмотрение условного потребителя
- транспортная задача называется открытой транспортной задачей с избыточным предложением. Она может быть приведена к закрытой задаче, если ввести в рассмотрение условного потребителя 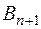 , величина запасов у которого:
, величина запасов у которого: 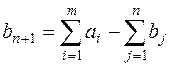 , а удельные транспортные затраты по перевозке груза от условного поставщика ко всем потребителям принимаются равными 0:
, а удельные транспортные затраты по перевозке груза от условного поставщика ко всем потребителям принимаются равными 0: 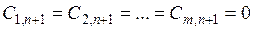 . Компоненты
. Компоненты 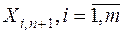 , найденного плана поставок означают количество товара, которое останется у поставщика
, найденного плана поставок означают количество товара, которое останется у поставщика 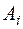 после того как потребности всех потребителей будут удовлетворены. При этом матрица планирования транспортной задачи дополняется одним столбцом
после того как потребности всех потребителей будут удовлетворены. При этом матрица планирования транспортной задачи дополняется одним столбцом
Определим тип задачи:
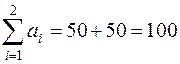 - суммарные запасы;
- суммарные запасы;
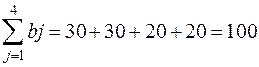 - суммарные потребности.
- суммарные потребности.
Т.к. 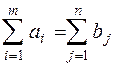 , то задача закрытая.
, то задача закрытая.
Не учитывая удельные транспортные затраты на перевозку груза, начинаем удовлетворять потребности 1-го потребителя B1 за счёт 1-го поставщика A1. Потребности потребителя B1 удовлетворены, а у поставщика A1 осталось 20 ед. товара, поэтому за счёт A1 пытаемся удовлетворить потребности B2 (переходим на клетку вправо). На складе A1 товара не осталось, а потребности B2 не удовлетворены, поэтому удовлетворяем его потребности за счёт склада А2 (перемещаемся на клетку вниз). Потребности В2 удовлетворены, а на складе А2 осталось 40 ед. товара, поэтому удовлетворяем за счёт его потребности В3 (переходим на клетку вправо). Потребности В3 удовлетворены, а на складе А2 осталось 20 ед. товара, поэтому удовлетворяем за счёт его потребности В4 (переходим на клетку вправо). Всего 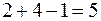 базисных клеток.
базисных клеток.
Начальный план перевозок, полученный методом северо-западного угла, представлен в таблице 12:
Таблица 12
| 4 30 |  2 20 2 20
| 1 | 3 | |
| 2 | 3 10 | 4 20 | 1 20 | |
Клетка называется занятой, если в ней находится какой-либо объём перевозок. Базисом транспортной задачи называется набор 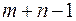 занятых клеток, обладающих следующим свойством: в каждой строке и в каждом столбце должна быть хотя бы одна базисная клетка. Потенциалами строк и столбцов относительно базиса Б называется набор чисел
занятых клеток, обладающих следующим свойством: в каждой строке и в каждом столбце должна быть хотя бы одна базисная клетка. Потенциалами строк и столбцов относительно базиса Б называется набор чисел 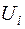 ,
, 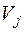 , удовлетворяющие уравнению:
, удовлетворяющие уравнению:
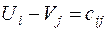 , если
, если 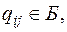 (1)
(1)
где 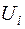 - потенциал
- потенциал 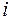 -ой строки;
-ой строки; 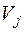 - потенциал
- потенциал 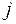 -ого столбца.
-ого столбца.
После того как найдены потенциалы строк и столбцов определяем относительные оценки небазисных клеток по формуле:
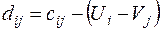 , если
, если 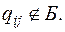 (2)
(2)
Если нет 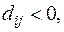 то текущий план оптимален.
то текущий план оптимален.
Проверим на оптимальность начальный план перевозок, представленный в таблице 12.
По базисным клеткам по формуле (1) составим систему уравнений для определения потенциалов строк и столбцов:
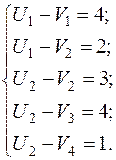
Эта система содержит 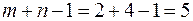 уравнений с
уравнений с 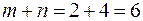 неизвестными. Т.к. уравнений на 1 меньше чем неизвестных, система является неопределённой и одному неизвестному (которое чаще всего встречается) присваивают нулевое значение. После этого остальные потенциалы определяются однозначно.
неизвестными. Т.к. уравнений на 1 меньше чем неизвестных, система является неопределённой и одному неизвестному (которое чаще всего встречается) присваивают нулевое значение. После этого остальные потенциалы определяются однозначно.
Пусть 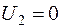 , тогда
, тогда 
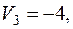
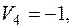
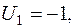
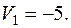
Вычисляем по формуле (2) относительные оценки небазисных клеток:
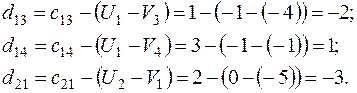
Т.к. есть 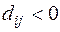 , текущий план не оптимален.
, текущий план не оптимален.
В таблице 13 представлен начальный план перевозок, проверенный на оптимальность:
Таблица 13
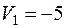
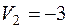
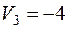
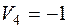
| 4 30 |  2 20 2 20
| 1 -2 | 3 1 | |
| 2 -3 | 3 10 | 4 20 | 1 20 | |

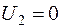
Примечание: в правом нижнем угле указаны относительные оценки небазисных клеток.
Если план не оптимален, то выбираем клетку с наименьшей отрицательной относительной оценкой и включаем эту клетку в базис, т.е. 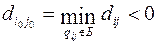
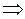
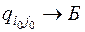 . (3)
. (3)
Чтобы найти клетку, исключаемую из базиса, строим цикл пересчёта, который начинается с клетки 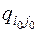 и в дальнейшем проходит по базисным клеткам. Циклом называется замкнутая ломаная линия, вершины которой расположены в базисных клетках, а звенья – вдоль строк и столбцов, причём в каждой строке и каждом столбце соединяются либо две клетки, либо не одной. Если ломаная цикла пересекается, то точки пересечения вершинами не являются.
и в дальнейшем проходит по базисным клеткам. Циклом называется замкнутая ломаная линия, вершины которой расположены в базисных клетках, а звенья – вдоль строк и столбцов, причём в каждой строке и каждом столбце соединяются либо две клетки, либо не одной. Если ломаная цикла пересекается, то точки пересечения вершинами не являются.
В клетках, расположенных в вершинах цикла перераспределяем объёмы перевозок. К клетке вводимой в базис добавляем некоторую величину Θ (промежуточная рента), из следующей клетки Θ вычитаем, далее прибавляем и т.д. Промежуточная рента Θ равна минимальному объёму перевозок в тех клетках, где Θ вычитаем. Базисная клетка, в которой объём перевозок равен Θ выходит из базиса (если таких клеток несколько, то выходит одна, а в других объёмы перевозок равны 0). Следующий план будет дешевле предыдущего на величину
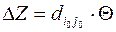 . (4)
. (4)
Произведем перераспределение перевозок и доведем до оптимального план из таблицы 13.
Выбираем наименьшую отрицательную относительную оценку ( 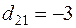 ) и эту клетку включаем в базис (
) и эту клетку включаем в базис ( 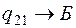 ).
).
В таблице 14 построен цикл пересчёта и перераспределены перевозки:
Таблица 14
4 30
 -Θ -Θ
|  2 20
+Θ 2 20
+Θ
| 1 | 3 | |
| 2 +Θ | 3 10 -Θ | 4 20 | 1 20 | |
Определим промежуточную ренту Θ:
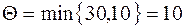
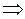
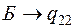 .
.
Уменьшение транспортных затрат: 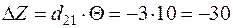 .
.
Новый план перевозок записан в таблице 15(изменяем объёмы перевозок только в клетках, находящихся в вершинах цикла):
Таблица 15
| 4 20 |  2 30 2 30
| 1 | 3 | |
| 2 10 | 3 | 4 20 | 1 20 | |
Проверим новый план на оптимальность.
Потенциалы строк и столбцов:
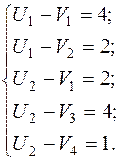
Пусть 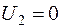 , тогда
, тогда 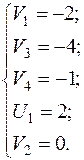
Относительные оценки:
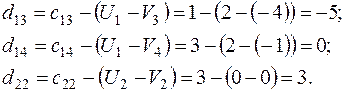
В таблице 16 представлен начальный план перевозок, проверенный на оптимальность:
Таблица 16
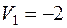
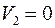
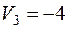
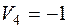
| 4 20 |  2 30 2 30
| 1 -5 | 3 0 | |
| 2 10 | 3 3 | 4 20 | 1 20 | |
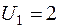
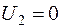
Т.к. есть 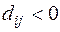 , текущий план не оптимален. Вводим клетку
, текущий план не оптимален. Вводим клетку 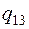 в базис и строим цикл пересчёта.
в базис и строим цикл пересчёта.
Новый план перевозок представлен в таблице 17.
Таблица 17
 4 20
-Θ 4 20
-Θ
|  2 30 2 30
| 1 +Θ | 3 | |
| 2 10 +Θ | 3 | 4 20 -Θ | 1 20 | |
Определим промежуточную ренту:
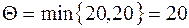
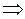
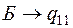 .
.
Уменьшение транспортных затрат: 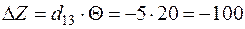 .
.
Новый план перевозок (смотри таблицу 18):
Таблица 18
| 4 |  2 30 2 30
| 1 20 | 3 | |
| 2 30 | 3 | 4 0 | 1 20 | |
Проверим новый план на оптимальность.
Потенциалы строк и столбцов:
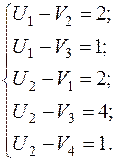 Пусть
Пусть 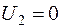 , тогда
, тогда 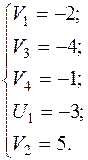
Относительные оценки:
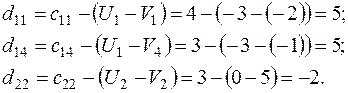
План перевозок имеет вид (смотри таблицу 19):
Таблица 19
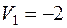
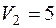
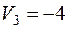
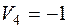
| 4 5 |  2 30 2 30
| 1 20 | 3 5 | |
| 2 30 | 3 -2 | 4 0 | 1 20 | |
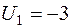
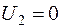
Т.к. есть 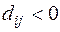 , текущий план не оптимален. Вводим клетку
, текущий план не оптимален. Вводим клетку 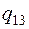 в базис и строим цикл пересчёта (смотри таблицу20).
в базис и строим цикл пересчёта (смотри таблицу20).
Таблица 20
| 4 |   2 30
-Θ 2 30
-Θ
| 1 20 +Θ | 3 | |
| 2 30 | 3 +Θ | 4 0 -Θ | 1 20 | |
Определим промежуточную ренту:
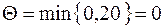
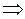
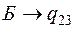 .
.
Уменьшение транспортных затрат: 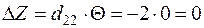 .
.
Новый план перевозок (смотри таблицу 21):
Таблица 21
| 4 |  2 30 2 30
| 1 20 | 3 | |
| 2 30 | 3 0 | 4 | 1 20 | |
Проверим новый план на оптимальность.
Потенциалы строк и столбцов:
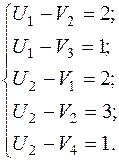 Пусть
Пусть 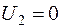 , тогда
, тогда 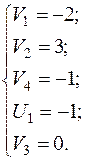
Относительные оценки:
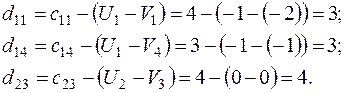
Т.к. нет 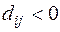 , текущий план оптимален.
, текущий план оптимален.
Стоимость перевозок по этому плану:
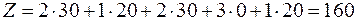 .
.
Минимальная стоимость перевозок в размере 160 руб. достигается, если перевезти с 1-го склада во 2-ой магазин 30 ед. товара и в 3-ий магазин 20 ед., а со 2-го склада – 30 ед. в 1-ый магазин и 20 ед. в 4-ый магазин.
Модели сетевого планирования и управления
Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ, заданный в форме сети.
Работа в сетевом планировании и управлении (СПУ):
1) протяженный во времени процесс, требующий затрат ресурсов (действительная работа);
2) протяженный во времени процесс, не требующий затрат труда (ожидание);
3) логическая связь между работами, не требующая затрат времени и ресурсов (фиктивная работа).
Событие – отдельный этап выполнения проекта, не имеющий продолжительности. На сетевом графике (графе) события изображаются вершинами, работы – ориентированными дугами.
Задача 7. Для сетевого графика изображенного на рисунке 10 определить временные параметры работы (2-4).
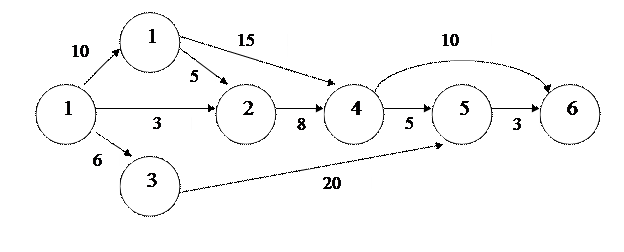 Рис.10. План выполнения некоторого комплекса взаимосвязанных работ
Рис.10. План выполнения некоторого комплекса взаимосвязанных работ
Определим критический путь (самый продолжительный из V1 в V6). Его длина определяет продолжительность выполнения всего комплекса работ. Продолжительности полных путей для сетевого графика представлены в таблице 22.
Таблица 22
| Полный путь | Продолжительность |
| 0-3-5-6 0-1-2-4-6 0-1-2-4-5-6 0-1-4-5-6 0-1-4-6 0-2-4-6 0-2-4-5-6 | 6+20+3=29 10+5+8+10=33 10+5+8+5+3=31 10+15+5+3=33 10+15+10=35 3+8+10=21 3+8+5+3=19 |
Путь 0-1-4-6 имеет наибольшую продолжительность 35 сут. Следовательно, выполнение всех работ закончится через 35 сут. События 0, 1, 4, 6 –критические, а (0,1), (1,4), (4,6) – критические работы.
Временные параметры событий
Ранний (ожидаемый) срок 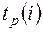 свершения
свершения 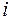 -го события определяется продолжительностью максимального пути, предшествующего этому событию, т.е.
-го события определяется продолжительностью максимального пути, предшествующего этому событию, т.е.
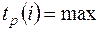
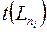 , (1)
, (1)
где 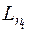 - любой путь, предшествующий
- любой путь, предшествующий 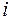 -му событию.
-му событию.
Поздний (предельный) срок 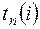 свершения
свершения 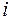 -го события определяется как разность между длиной критического пути и длиной максимального пути, последующего за этим событием, т.е.
-го события определяется как разность между длиной критического пути и длиной максимального пути, последующего за этим событием, т.е.
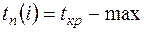
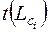 , (2)
, (2)
где 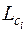 - любой путь, следующий за
- любой путь, следующий за 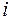 -м событием.
-м событием.
Резерв времени 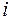 -го события
-го события 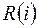 определяется как разность между поздним и ранним сроками его свершения, т.е
определяется как разность между поздним и ранним сроками его свершения, т.е
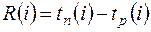 . (3)
. (3)
Он показывает, на какое время можно задержать наступление этого события, не увеличивая времени выполнения всего комплекса работ. Критические события резервов времени не имеют.
Временные параметры событий для сетевого графика из рисунка 10 представлены в таблице 23.
Таблица 23
| №собы- тия | Сроки свершения события, сут | Резерв времени
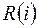 , сут. , сут.
| |
ранний 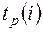
| поздний 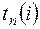
| ||
Для вершины 2 существует два предшествующих пути:
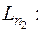
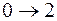 и
и 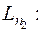
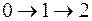
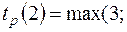
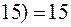 .
.
При определении поздних сроков свершения событий движемся по сети в обратном направлении.
Для вершины 4 существует два последующих пути:
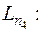
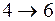 и
и 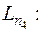
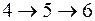
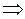
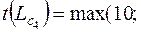
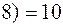
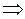
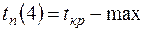
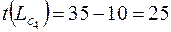 .
.
Временные параметры работ
Ранний срок 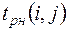 начала работы
начала работы 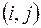 совпадает с ранним сроком наступления предшествующего события, т.е.
совпадает с ранним сроком наступления предшествующего события, т.е.
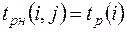 . (3)
. (3)
Ранний срок окончания 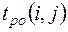 равен сумме раннего срока начала и времени продолжительности работы, т.е.
равен сумме раннего срока начала и времени продолжительности работы, т.е.
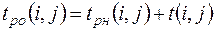 . (4)
. (4)
Поздний срок окончания 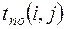 равен позднему сроку наступления следующего события, т.е.
равен позднему сроку наступления следующего события, т.е. 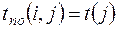 . (5)
. (5)
Поздний срок начала работы 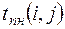 равен разности между поздним сроком окончания и временем выполнения работы, т.е.
равен разности между поздним сроком окончания и временем выполнения работы, т.е.
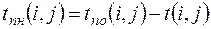 . (6)
. (6)
Резервы времени работ
а) Полный резерв времени 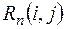 показывает, на сколько можно увеличить время выполнения данной работы, не увеличивая времени выполнения всего комплекса работ:
показывает, на сколько можно увеличить время выполнения данной работы, не увеличивая времени выполнения всего комплекса работ:
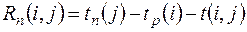 . (7)
. (7)
б) Частный резерв времени I-го вида 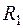 - часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока её начального события:
- часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока её начального события:
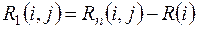 . (8)
. (8)
в) Частный резерв времени II-го вида 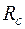 (свободный резерв) - часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока её конечного события:
(свободный резерв) - часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока её конечного события:
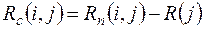 . (9)
. (9)
г) Независимый резерв времени 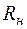 - часть полного резерва времени, на которую можно увеличить продолжительность работы, при условии, что все предшествующие события заканчиваются в поздние сроки, а все последующие начинаются в ранние:
- часть полного резерва времени, на которую можно увеличить продолжительность работы, при условии, что все предшествующие события заканчиваются в поздние сроки, а все последующие начинаются в ранние:
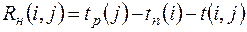 . (10)
. (10)
Он используется для увеличения продолжительности только данной работы.
Если на критическом пути лежит начальное событие, то 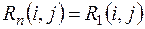 , если конечное -
, если конечное - 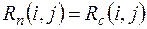 , если начальное и конечное события лежат на критическом пути,
, если начальное и конечное события лежат на критическом пути, 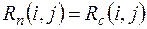 сама работа не принадлежит этому пути, то все резервы времени равны
сама работа не принадлежит этому пути, то все резервы времени равны 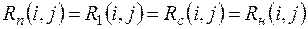 .
.
Вычислим временные параметры работы (2,4) для сетевого графика из сетевого графика из рисунка 10..
Ранний срок начала работы 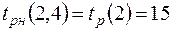 .
.
Ранний срок окончания работы 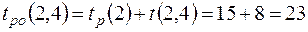 .
.
Поздний срок окончания работы 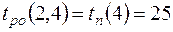 .
.
Поздний срок начала работы 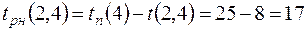
Полный резерв времени 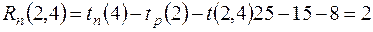 , т.е. при увеличении продолжительности работы (2,4) на 2 сут. резервы времени путей, содержащих эту работу, уменьшатся на 2 сут., а продолжительность выполнения всего комплекса работ не изменится.
, т.е. при увеличении продолжительности работы (2,4) на 2 сут. резервы времени путей, содержащих эту работу, уменьшатся на 2 сут., а продолжительность выполнения всего комплекса работ не изменится.
Частный резерв времени I-го вида 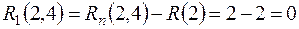 .
.
Свободный резерв времени 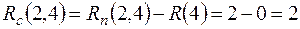 .
.
Независимый резерв времени 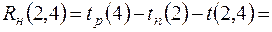
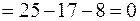 , т.е. продолжительность работы (2,4) не может быть увеличена без изменения резервов времени остальных работ.
, т.е. продолжительность работы (2,4) не может быть увеличена без изменения резервов времени остальных работ.
Действительно для работы (2,4) 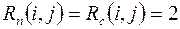
Замечание 5. Если 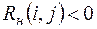 , то ставится прочерк.
, то ставится прочерк.
Дата добавления: 2014-11-29; просмотров: 1168;
